Презентация на тему Системы уравнений (11 класс)

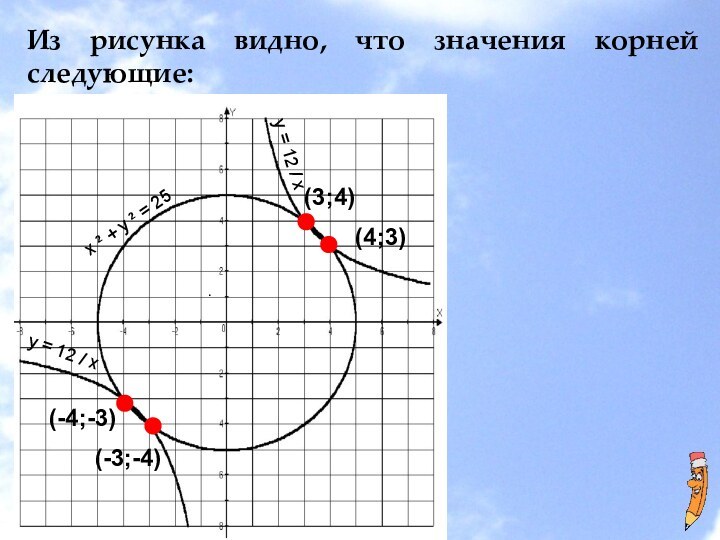
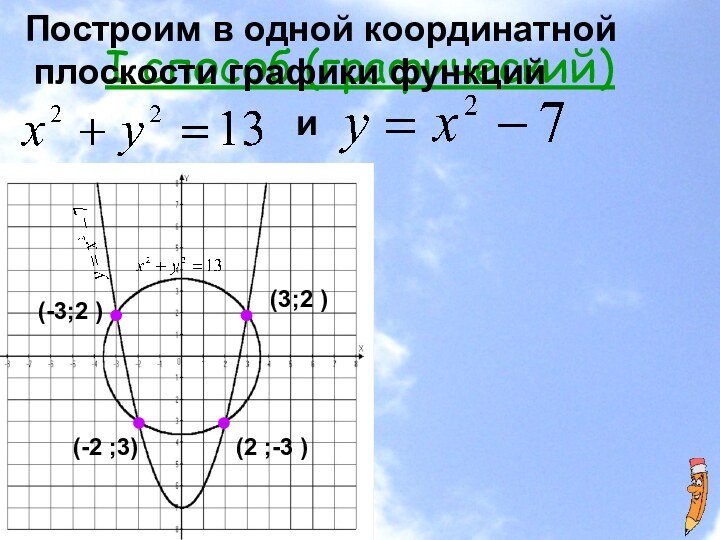
скобкой. Порядок уравнений не играет роли.
Например:

Системой уравнений называется множество уравнений, решаемых совместно.

называется множество пар (х;у), удовлетворяющих каждому уравнению.

Обозначение.

5х+3у=7
2х+3у=1

Решением системы
уравнений с 2 переменными

а другое второй.
Система уравнений вида:

х + у = а
ху = b.

Уравнение первой степени

Уравнение второй степени

3у = 1

2 х – =

Воспользуемся способом подстановки

у

1

2

выразим из второго уравнения у.

с одним неизвестным х:
4 у + х + 3у

2 х – 1 = у

-4(2х-1) +х+3(2х-1)=1

2

х + 3(2х-1)=1
2
х – 4 (2х-1) + х +

2

2

2

2

2

2

2

2

х + 8 = 0
2
√D = √23 – 4

х = = 1

1

23 + 7

30

х = = 1/15

2

23 - 7

30

1 находим:
у1 = 2 - 1
у2= 2

х

х

•1 = 1

8/15 = 1/15

данная система имеет две пары решений:
1) x1 = 1 ,

Ответ: ( 1; 1) ;(8/15 ; 1/15)

Пример:
x

2

2

= 0  и  у = 0 . Поэтому мы

x² + ( b/x )² = a
у = b/x

x² + y² = а
х у = b

<=>

уравнение:

x + b = ax , т. е.

2

4

4

2

2

2

2

x² — y² = а
xy

Подобным же образом решается и система:

x² — y² = а
xy = b.

графики функций

х ² + у ² = 25
х • у = 12

<=>

х ² + у ² = 25
у = 12 / х

² + у ² = 25
у = 12 /

у = 12 / х

(-4;-3)

(-3;-4)

(3;4)

(4;3)

сначала сложим с первым, а затем вычтем из первого.

<=>

× 2

неизвестными:

сложим эти уравнения, а далее вычтем из первых –

Ответ: (4;3) ; (-3;-4) ; (3;4) ; (-4;-3)

графики функций

(-3;2 )

(-2 ;3)

(3;2 )

(2 ;-3 )