- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Средняя линия треугольника. Свойство медиан треугольника
Содержание
- 2. Каким образом эти треугольники поделили на две
- 3. АСВОпределение. Средней линией треугольника называется отрезок, соединяющий
- 4. Теорема. Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны.Доказательство: АBC
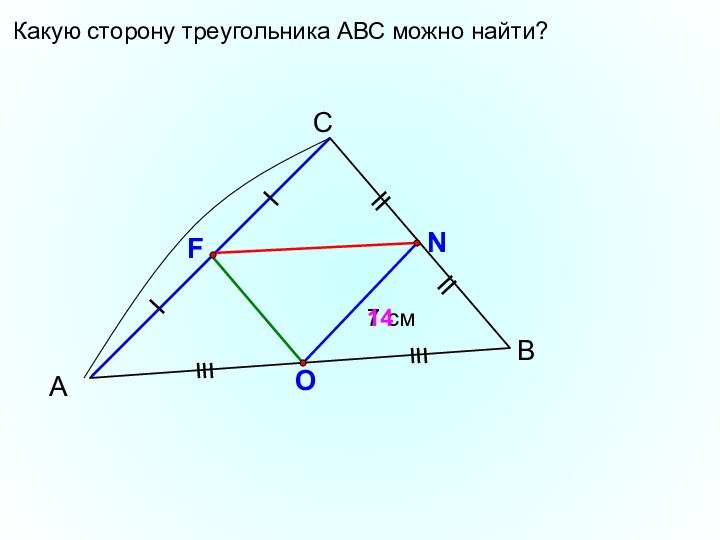
- 5. АСВ7 смFNO14Какую сторону треугольника АВС можно найти?
- 6. АСВ7 смFNO14Найдите стороны треугольника АВС.8 см5,5см1611
- 7. ВАС№ 566. Точки Р и Q –
- 8. АСВFNOНайдите периметр треугольника АВС, если периметр треугольника ОFN равен 23 см.Р=23см
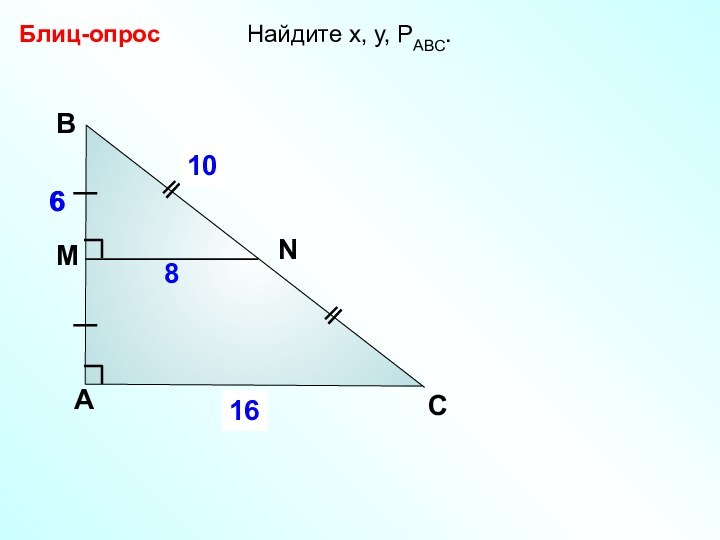
- 9. Найдите х, у, РАВС. Блиц-опросАВСx86МNy10616
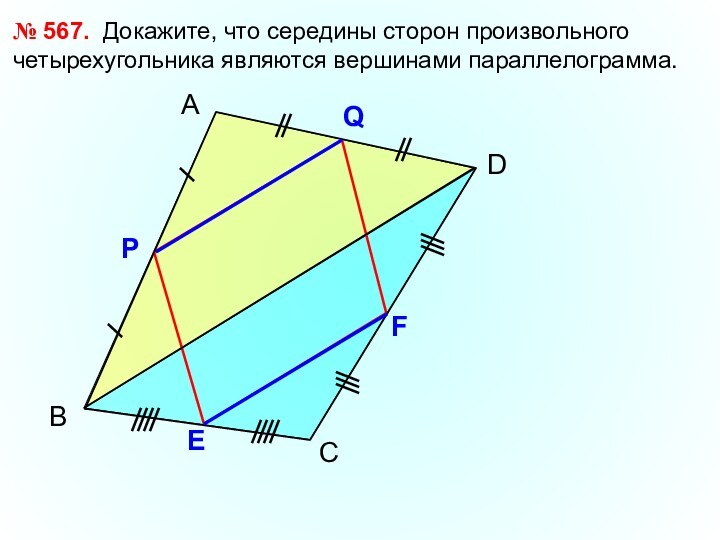
- 10. ВАD№ 567. Докажите, что середины сторон произвольного четырехугольника являются вершинами параллелограмма.С
- 11. ВАD№ 568. Докажите, что четырехугольник – ромб, если его вершинами являются середины сторон прямоугольника.С
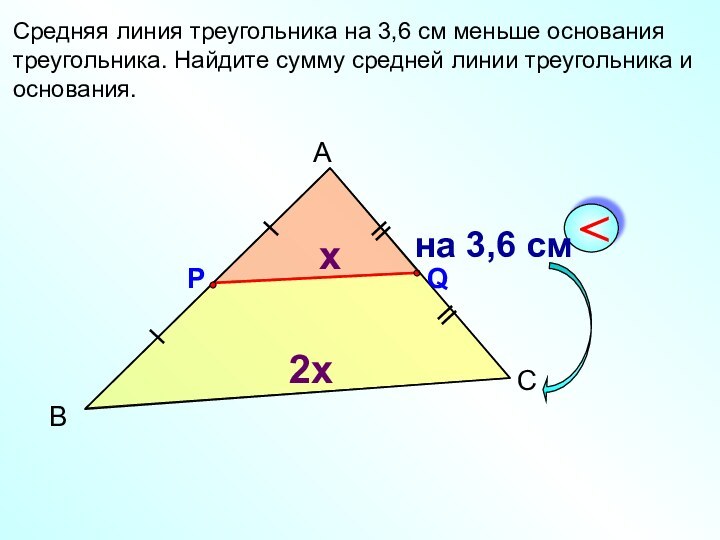
- 12. Средняя линия треугольника на 3,6 см меньше основания треугольника. Найдите сумму средней линии треугольника и основания.ВАСРQx2x
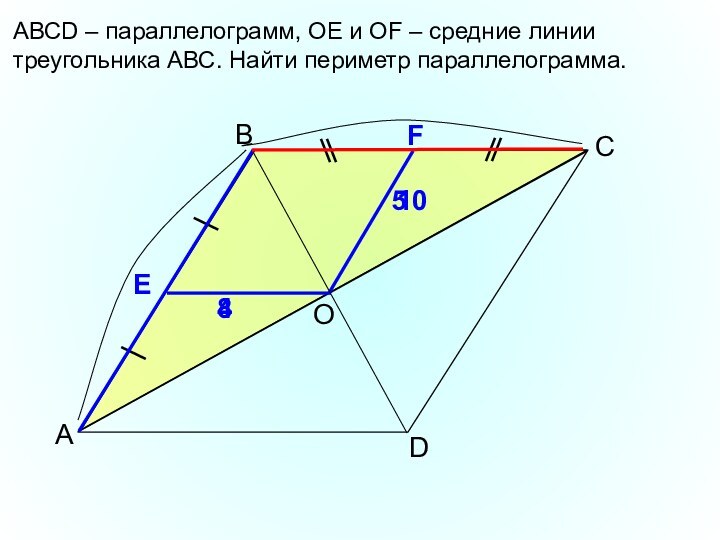
- 13. ВАDАВСD – параллелограмм, ОЕ и ОF – средние линии треугольника АВС. Найти периметр параллелограмма.СFЕО54108
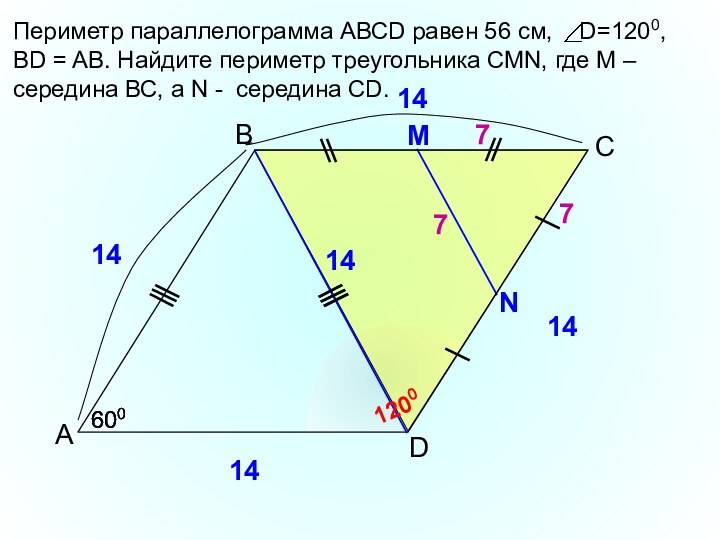
- 14. ВАDПериметр параллелограмма АВСD равен 56 см,
- 15. ВАDПериметр параллелограмма АВСD равен 60 см, а
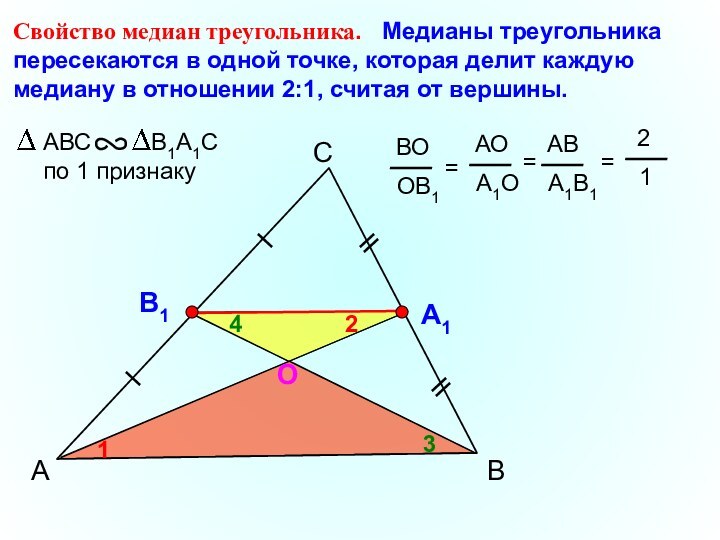
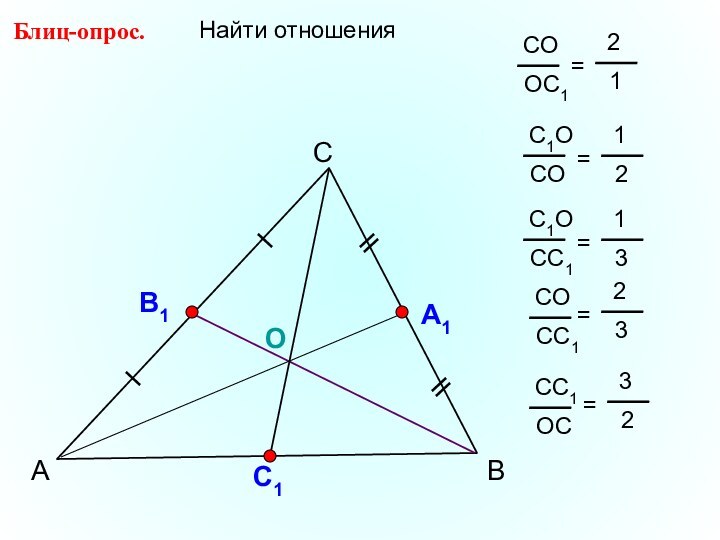
- 16. АСВСвойство медиан треугольника. Медианы треугольника пересекаются
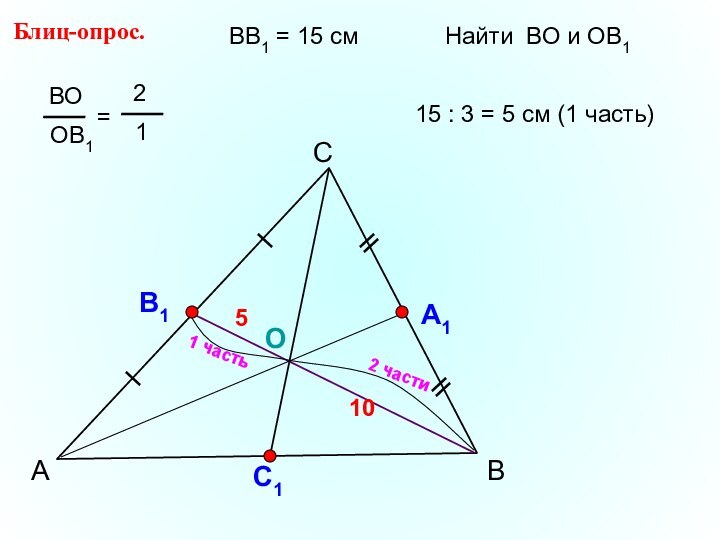
- 17. АСВБлиц-опрос. А1ОС1ВВ1 = 15 смНайти ВО
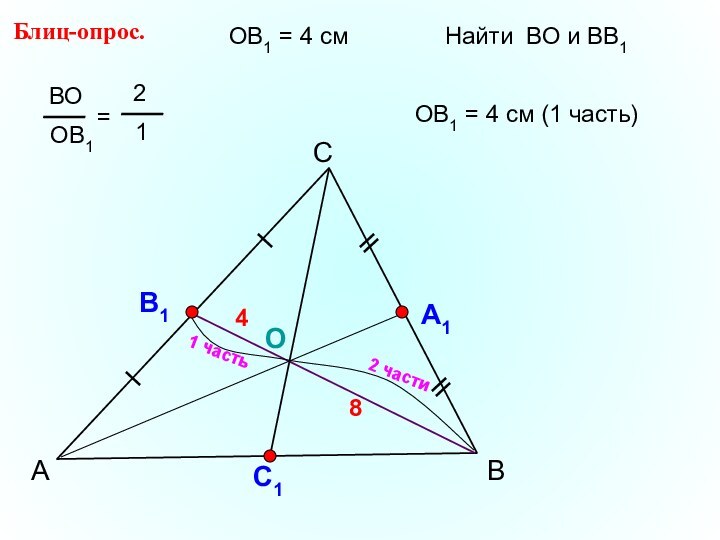
- 18. АСВБлиц-опрос. А1ОС1ОВ1 = 4 смНайти ВО и ВВ1 ОВ1 = 4 см (1 часть)84
- 19. АСВБлиц-опрос. А1ОС1ОС = 7 смНайти СО
- 20. Скачать презентацию
- 21. Похожие презентации
Каким образом эти треугольники поделили на две группы?









Слайд 3
А
С
В
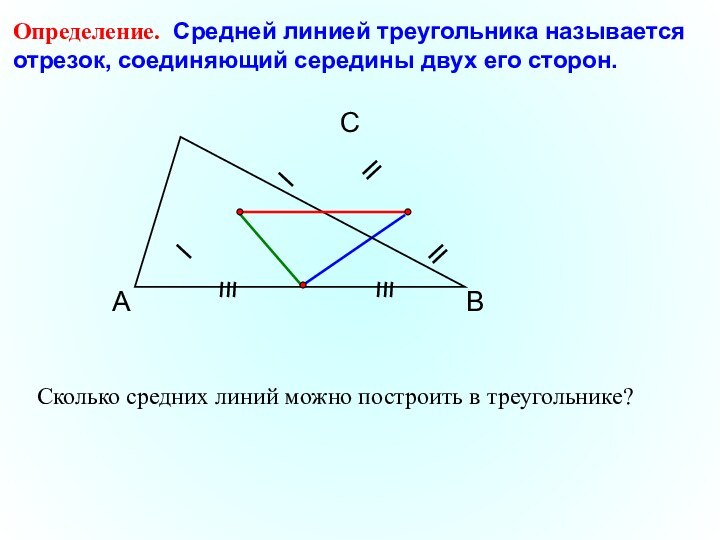
Определение. Средней линией треугольника называется отрезок, соединяющий середины
двух его сторон.
Сколько средних линий можно построить в треугольнике?
Слайд 4
Теорема. Средняя линия треугольника параллельна одной из его
сторон и равна половине этой стороны.
Доказательство:
А
B
C
Слайд 7
В
А
С
№ 566. Точки Р и Q – середины
сторон АВ и АС треугольника АВС. Найдите периметр треугольника
АВС, если периметр АРQ равен 21 см.Р=21см
Р
Q
Слайд 10
В
А
D
№ 567. Докажите, что середины сторон произвольного четырехугольника
являются вершинами параллелограмма.
С
Слайд 11
В
А
D
№ 568. Докажите, что четырехугольник – ромб, если
его вершинами являются середины сторон прямоугольника.
С
Слайд 12 Средняя линия треугольника на 3,6 см меньше основания
треугольника. Найдите сумму средней линии треугольника и основания.
В
А
С
Р
Q
x
2x
Слайд 13
В
А
D
АВСD – параллелограмм, ОЕ и ОF – средние
линии треугольника АВС. Найти периметр параллелограмма.
С
F
Е
О
5
4
10
8
Слайд 14
В
А
D
Периметр параллелограмма АВСD равен 56 см, D=1200,
BD
= AВ. Найдите периметр треугольника СМN, где М –
середина ВС, а N - середина СD.С
М
N
1200
600
600
600
14
14
14
7
7
7
Слайд 15
В
А
D
Периметр параллелограмма АВСD равен 60 см, а длина
его диагонали ВD равна 18 см. Точки К и
Р – середины сторон АD и АВ соответственно. Найдите периметр пятиугольника ВСDКР.С
К
Р
18
9
РАВСD=60см
рАВСD=30см
РВСDKP= ВС + СD + DK + BP + PK
9
Слайд 16
А
С
В
Свойство медиан треугольника. Медианы треугольника пересекаются в
одной точке, которая делит каждую медиану в отношении 2:1,
считая от вершины.АВ
А1В1