b, c – заданные числа, а≠0,
х – действительная переменная,
называется квадратичной функцией.Примеры:
1) у=5х+1 4) у=x3+7x-1
2) у=3х2-1 5) у=4х2
3) у=-2х2+х+3 6) у=-3х2+2х
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть







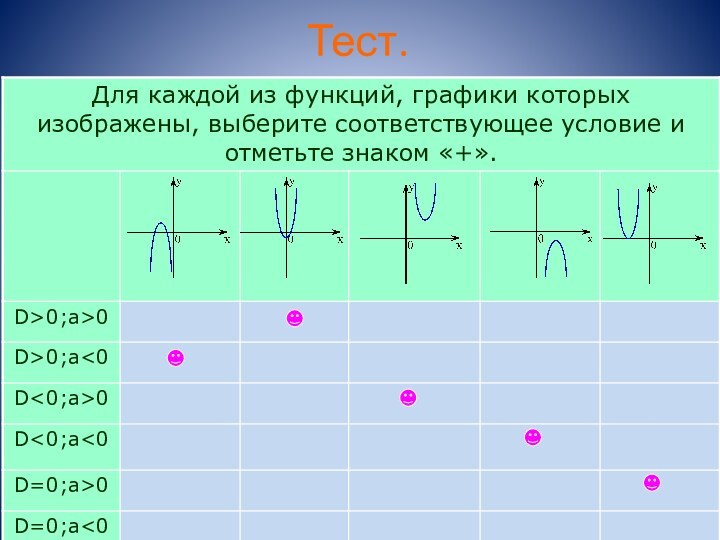






Например:
у=2х²+4х-1 – графиком является парабола, ветви которой направлены вверх (т.к. а=2, а>0).
у= -7х²-х+3 – графиком является парабола, ветви которой направлены вниз (т.к. а=-7, а<0).
у
0
х
у
0
х
3.
Провести ось симметрии.
4.
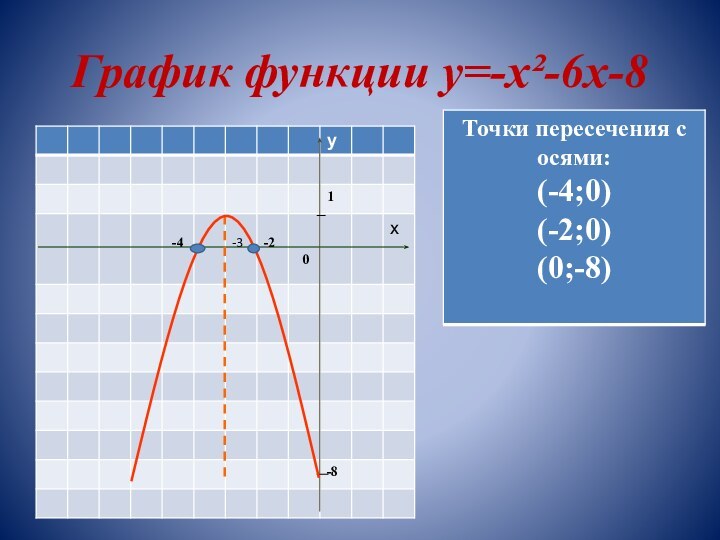
Определить точки пересечения графика
функции с осью Ох, т.е. найти нули
функции.
5.
Составить таблицу значений функции
с учетом оси симметрии параболы.