Слайд 2
План лекции:
1. Виды связей между явлениями
2. Простейшие методы
изучения стохастических связей
3. Статистическое моделирование связи методом корреляционного и
регрессионного анализа
а) однофакторные модели
б) многофакторные модели
4.Непараметрические методы
Слайд 3
1. Виды связей между явлениями
Знание характера и силы
связей позволяет управлять социально-экономическими явлениями и процессами и предсказать
их развитие
Слайд 4
Среди многих форм связей важнейшей является причинная. Причинно-следственные
отношения - это связь явлений и процессов, когда изменение
одного из них (причины) ведет к изменению другого (следствия).
Причина- это совокупность условий, обстоятельств, действие которых приводит к появлению следствия.
Слайд 5
Между различными явлениями и их признаками выделяют два
типа связей:
функциональную (жестко детерминированную)
и статистическую (стохастически детерминированную)
Слайд 6
Связь признака у с признаком х называется функциональной,
если каждому возможному значению независимого признака х соответствует одно
или несколько строго определенных значений зависимого признака у. Определение функциональной связи может быть легко обобщено для случая многих признаков х1, х2, ..., хn.
Функциональную связь можно представить уравнением:
yi=f(xi),
где yi- результативный признак (i=1,...,n); f(xi)- известная функция связи результативного и факторного признаков; х1- факторный признак.
Слайд 7
Стохастическая связь- это связь между величинами, при которой

одна из них, случайная величина у, реагирует на изменение
другой величины х или других величин х1, х2,..., хn (случайных или неслучайных) изменением закона распределения. Это обусловливается тем, что зависимая переменная (результативный признак), кроме рассматриваемых независимых, подвержен влиянию ряда неучтенных или неконтролируемых (случайных) факторов, а также некоторых неизбежных ошибок измерения переменных.
Поскольку значения зависимой переменной подвержены случайному разбросу, они не могут быть предсказаны с достаточной точностью, а только указаны с определенной вероятностью.
Модель стохастической связи может быть представлена в общем виде уравнением:
где - расчетное значение результативного признака; f (xi)- часть результативного признака, сформировавшаяся под воздействием учтенных известных факторных признаков (одного или множества), находящихся в стохастической связи с признаком;
εi- часть результативного признака, возникшая вследствие действия неконтролируемых или неучтенных факторов, а также измерения признаков неизбежно сопровождающегося некоторыми случайными ошибками.
Слайд 8
Частные случаи стохастических связей- это корреляционная и регрессионная.
Корреляция-
это статистическая зависимость между случайными величинами, не имеющими строго
функционального характера. Корреляционный анализ имеет своей задачей определение тесноты связи между двумя признаками (при парной корреляции) и между результативным и несколькими факторными.
Регрессионный анализ - заключается в определении аналитического выражения связи.
Корреляционный анализ: измерение тесноты связи, направления и установления аналитического выражения связи.
Слайд 9
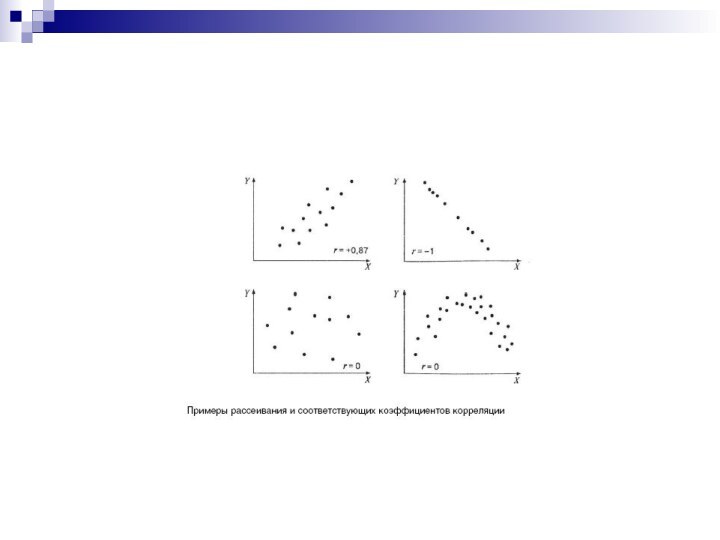
Прямые и обратные связи.
Прямолинейные и криволинейные связи.
Однофакторные
и многофакторные связи.
Слайд 10
2. Простейшие методы изучения стохастических связей.
Метод сопоставления двух
параллельных рядов.
Метод аналитических группировок
Слайд 11
3. Статистическое моделирование связи методом корреляционного и регрессионного
анализа.
а) Двухмерная линейная модель корреляционного и регрессионного анализа (однофакторный
линейный корреляционный и регрессионный анализ).
Наиболее разработанной является методология так называемой парной корреляции, рассматривающая влияние вариации факторного признака х на результативный признак у и представляющая собой однофакторный корреляционный и регрессионный анализ.
Слайд 12
Выбор типа функции может опираться на теоретические знания
об изучаемом явлении, опыт предыдущих аналогичных исследований, или осуществляться
эмпирически — перебором и оценкой функций разных типов и т.п.
Слайд 15
Уравнение однофакторной (парной) линейной корреляционной связи имеет вид:
где — теоретические значения результативного признака, полученные по уравнению регрессии; а0, а1 – коэффициенты (параметры) уравнения регрессии.
Поскольку а0 является средним значением у в точке х = 0, экономическая интерпретация часто затруднена или вообще невозможна.
Слайд 16
Интерпретация:
Коэффициент парной линейной регрессии а1 имеет смысл показателя
силы связи между вариацией факторного признака х и вариацией
результативного признака у. Уравнение показывает среднее значение изменения результативного признака у при изменении факторного признака х на одну единицу его измерения, т.е. вариацию у , приходящуюся на единицу вариации х. Знак а1 указывает направление этого изменения.
Слайд 18
Проверка адекватности регрессионной модели. Для практического использования моделей
регрессии большое значение имеет их адекватность, т.е. соответствие фактическим
статистическим данным.
При численности объектов анализа до 30 единиц возникает необходимость проверки значимости (существенности) каждого коэффициента регрессии. При этом выясняют насколько вычисленные параметры характерны для отображения комплекса условий: не являются ли полученные значения параметров результатами действия случайных причин.
Слайд 20
Проверка адекватности регрессионной модели может быть дополнена корреляционным
анализом. Для этого необходимо определить тесноту корреляционной связи между
переменными х и у .
Теснота корреляционной связи, как и любой другой, может быть измерена эмпирическим корреляционным отношением ηэ, когда δ2 (межгрупповая дисперсия) характеризует отклонения групповых средних результативного признака от общей средней: .
Говоря о корреляционном отношении как о показателе измерения тесноты зависимости, следует отличать от эмпирического корреляционного отношения — теоретическое.
Слайд 22
Теоретическое корреляционное отношение применяется для измерения тесноты связи
при линейной и криволинейной зависимостях между результативным и факторным
признаком. При криволинейных связях теоретическое корреляционное отношение, исчисляемое по формулам часто называют индексом корреляции R. При значительной корреляции расчет по формулам (1.6) и (1.7) значительно проще, так как отклонение (), как правило, по значению меньше, чем отклонение ().
Корреляционное отношение может находиться в пределах от 0 до 1, т.е. (). Чем ближе корреляционное отношение к 1, тем связь между признаками теснее.
Кроме того, при линейной форме уравнения применяется другой показатель тесноты связи — линейный коэффициент корреляции.
Слайд 24
Факт совпадений и несовпадений значений теоретического корреляционного отношения
η и линейного коэффициента корреляции r используется для оценки
формы связи..
Посредством теоретического корреляционного отношения измеряется теснота связи любой формы, а с помощью линейного коэффициента корреляции — только прямолинейной. Следовательно, значения η и r совпадают только при наличии прямолинейной связи. Несовпадение этих величин свидетельствует, что связь между изучаемыми признаками не прямолинейная, а криволинейная. Установлено, что если разность квадратов η2 и r2 не превышает 0,1, то гипотезу о прямолинейной форме связи можно считать подтвержденной.
Слайд 25
Показатели тесноты связи, исчисленные по данным сравнительно небольшой
статистической совокупности, могут искажаться действием случайных причин. Это вызывает
необходимость проверки их существенности, дающей возможность распространять выводы по результатам выборки на генеральную совокупность.
Для оценки значимости коэффициента корреляции r используют t-критерий Стьюдента, который применяется при t-распределении, отличном от нормального.
Слайд 26
При линейной однофакторной связи t-критерий можно рассчитать по
формуле:
(1.10)
где (n—2) — число степеней свободы при заданном уровне значимости α и объеме выборки n.
Полученное значение tрасч сравнивают с табличным значением t-критерия (для α = 0,05 и 0,01). Если рассчитанное значение tрасч превосходит табличное значение критерия tтабл, то практически невероятно, что найденное значение обусловлено только случайными колебаниями (т.е. отклоняется гипотеза о его случайности).
Слайд 27
б) Многофакторный корреляционный и регрессионный анализ.
Между факторами
существуют сложные взаимосвязи, поэтому их влияние комплексное и его
нельзя рассматривать как простую сумму изолированных влияний.
Многофакторный корреляционный и регрессионный анализ позволяет оценить меру влияния на исследуемый результативный показатель каждого из включенных в модель (уравнение) факторов при фиксированном положении (на среднем уровне) остальных факторов, а также при любых возможных сочетаниях факторов с определенной степенью точности найти теоретическое значение этого показателя (важным условием является отсутствие между факторами функциональной связи).
Слайд 28
Математически задача формулируется следующим образом. Требуется найти аналитическое
выражение, наилучшим образом отражающее установленную теоретическим анализом связь независимых
признаков с результативным, т.е. функцию
Слайд 37
Оценку значимости коэффициентов регрессии с помощью t-критерия используют
для завершения отбора существенных факторов в процессе многошагового регрессионного
анализа. Он заключается в том, что после оценки значимости всех коэффициентов регрессии из модели исключают тот фактор, коэффициент при котором незначим и имеет наименьшее значение критерия. Затем уравнение регрессии строится без исключенного фактора, и снова проводится оценка адекватности уравнения и значимости коэффициентов регрессии.
Такой процесс длится до тех пор, пока все коэффициенты регрессии не окажутся значимыми, что свидетельствует о наличии в регрессионной модели только существенных факторов. В некоторых случаях расчетное значение tрасч находится вблизи tтабл поэтому с точки зрения содержательности модели такой фактор можно оставить для последующей проверки его значимости в сочетании с другим набором факторов.
Слайд 38
Однако на основе коэффициентов регрессии нельзя сказать какой
из факторных признаков оказывает наибольшее влияние на результативный признак,
так как коэффициенты регрессии между собой не сопоставимы, поскольку они измерены разными единицами. На их основе нельзя также установить в развитии каких факторных признаков заложены наиболее крупные резервы изменения результативного показателя, потому что в коэффициентах регрессии не учтена вариация факторных признаков.
Чтобы иметь возможность судить о сравнительной силе влияния отдельных факторов и о тех резервах, которые в них заложены, должны быть вычислены частные коэффициенты эластичности Эi,, а также бета-коэффициенты βi.
Слайд 41
Многофакторный корреляционный и регрессионный анализ может быть использован
в экономико-статистических исследованиях:
•для приближенной оценки фактического и заданного уровней;
•в
качестве укрупненного норматива (для этого достаточно в уравнение регрессии подставить вместо фактических значений факторов их средние значения);
•для выявления резервов производства;
•для проведения межзаводского сравнительного анализа и выявления на его основе скрытых возможностей предприятий;
•для краткосрочного прогнозирования развития производства и др.
Слайд 42
4. Непараметрические методы
непараметрические методы, с помощью которых устанавливается
связь между качественными (атрибутивными) признаками. Сфера их применения шире,
чем параметрических, поскольку не требуется соблюдения условия нормальности распределения зависимой переменной, однако при этом снижается глубина исследования связей. При изучении зависимости между качественными признаками не ставится задача представления ее уравнением. Здесь речь идет только об установлении наличия связи и измерении ее тесноты.
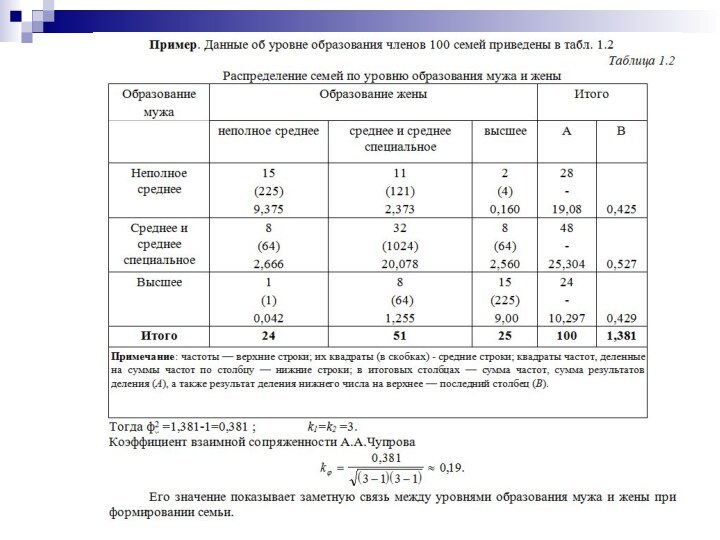
В практике экономических исследований приходится иногда анализировать связи между альтернативными признаками, представленными только группами с противоположными (взаимоисключающими) характеристиками. Тесноту связи в этом случае можно оценить, вычислив коэффициент ассоциации.