- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Свойства параллельных прямых
Содержание
- 2. Цели урока:Рассмотреть свойства параллельных прямых.Показать учащимся применение
- 3. Работа у доски:Доказать, что через данную точку,
- 4. ТестИсключить лишние слова: Аксиома – это(очевидные, исходные,
- 5. Тест3. Что может быть следствием аксиомы или
- 6. Тестб) Если две прямые параллельны третьей прямой,
- 7. Тест5. Указать правильный ответ на вопрос:Если через
- 8. Проверяем ответы:Лишние слова: очевидно, принятые, объяснений, обоснованийаа, бб, в, е, жб
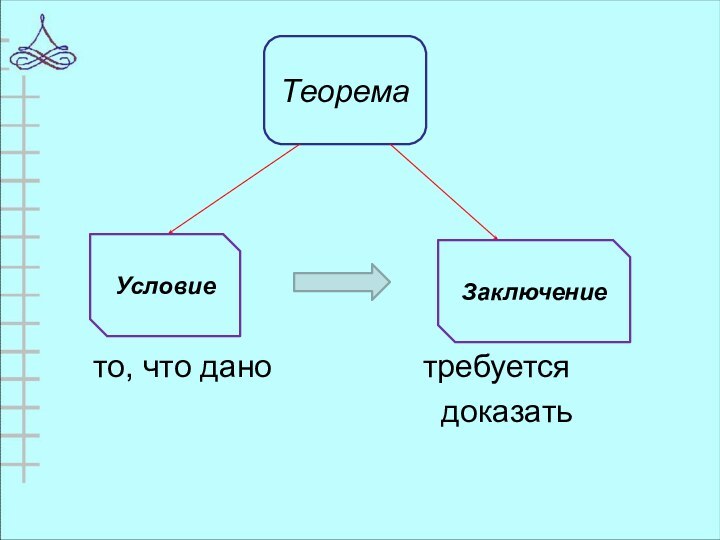
- 9. Задача Дано:ABǁCDНайти:
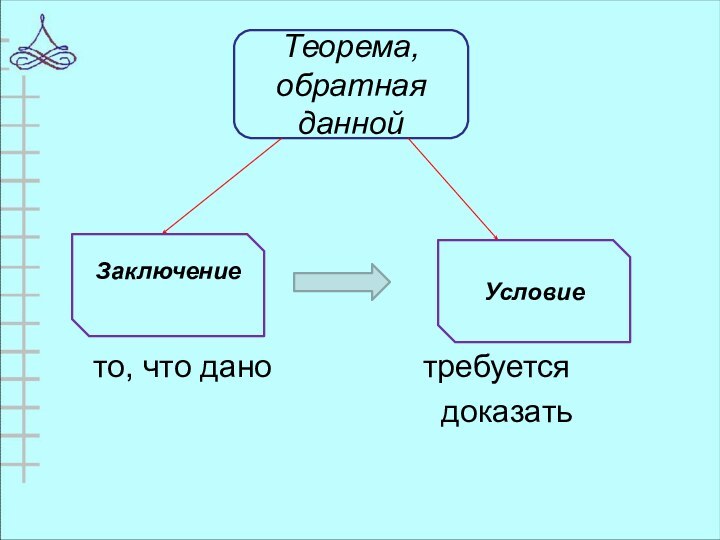
- 10. то, что дано
- 11. то, что дано
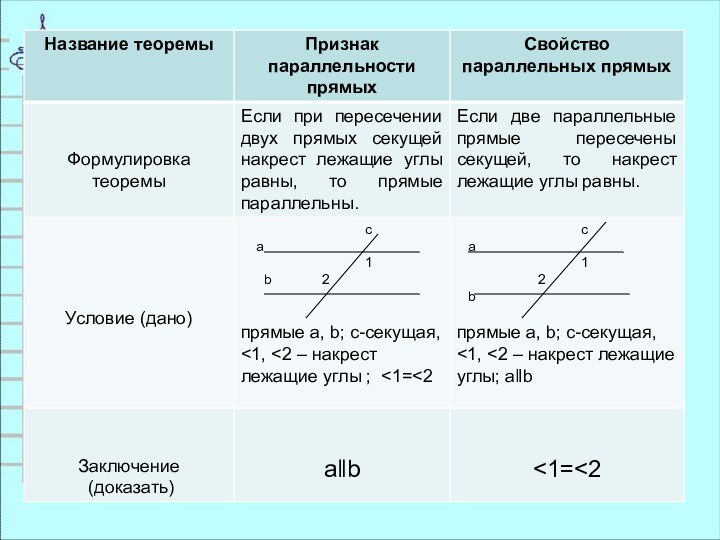
- 12. ТеоремаЕсли две параллельные прямые пересечены секущей, то
- 14. Работа в группахДокажите, что если прямая перпендикулярна
- 15. Задачи на готовых чертежах
- 16. Домашнее задание:§ 29, вопросы 12-15Дано: aǁb;
- 17. Скачать презентацию
- 18. Похожие презентации
Цели урока:Рассмотреть свойства параллельных прямых.Показать учащимся применение свойств параллельных прямых.Закрепить знания, умения и навыки учащихся по теме: «Аксиома параллельных прямых».












Слайд 2
Цели урока:
Рассмотреть свойства параллельных прямых.
Показать учащимся применение свойств
параллельных прямых.
«Аксиома параллельных прямых».
Слайд 3
Работа у доски:
Доказать, что через данную точку, не
лежащую на данной прямой, проходит прямая, параллельная данной.
Доказать, что
прямая, пересекающая одну из двух параллельных прямых, пересекает и другую.Доказать, что если две прямые параллельны третьей прямой, то они параллельны.
Слайд 4
Тест
Исключить лишние слова: Аксиома – это
(очевидные, исходные, принятые)
положения
геометрии, не требующие (объяснений,
доказательств, обоснований).
2. Выбрать окончание формулировки
аксиомыпараллельных прямых:
Через точку, не лежащую на данной прямой,
проходит:
а) только одна прямая, параллельная данной;
б) всегда проходит прямая, параллельная данной;
в) только одна прямая, не пересекающаяся с данной прямой.
Слайд 5
Тест
3. Что может быть следствием аксиомы или
теоремы?
Указать неверные ответы:
а) Утверждение, не требующее доказательства.
б) Новая
теорема, для доказательства которой использована аксиома или теорема.в) Утверждение, непосредственно выводимое из аксиомы или теоремы.
4. Укажите следствия аксиомы параллельных прямых:
а) Если отрезок или луч пересекает одну из двух параллельных прямых, то он пересекает и другую
Слайд 6
Тест
б) Если две прямые параллельны третьей прямой, то
они параллельны друг другу.
в) Если прямая пересекает одну из
двух параллельных прямых, то она пересекает и другуюг) Если три прямые параллельны, то любые две из них параллельны друг другу
д) Если две прямые не параллельны третьей прямой, то они не параллельны между собой.
е) Если прямая пересекает одну из параллельных прямых, то она не может не пересекать другую.
ж) Если две прямые параллельны третьей прямой, то они не могут быть не параллельны между собой
Слайд 7
Тест
5. Указать правильный ответ на вопрос:
Если через точку,
лежащую вне прямой, проведено
несколько прямых, то сколько из
них пересекаются с исходной прямой?
а) Неизвестно, так как не сказано, сколько прямых проведено через точку.
б) Все кроме параллельной прямой.
в) Все, которые имеют на рисунке точку пересечения с исходной прямой
Слайд 12
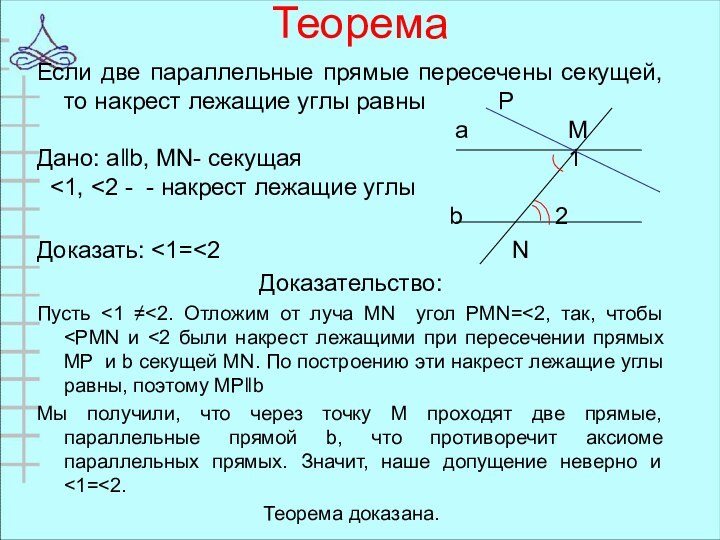
Теорема
Если две параллельные прямые пересечены секущей, то накрест
лежащие углы равны P
а М
Дано: аǁb, MN- секущая 1
<1, <2 - - накрест лежащие углы
b 2
Доказать: <1=<2 N
Доказательство:
Пусть <1 ≠<2. Отложим от луча MN угол PMN=<2, так, чтобы
Теорема доказана.
Слайд 14
Работа в группах
Докажите, что если прямая перпендикулярна к
одной из двух параллельных прямых , то она перпендикулярна
и другой.Сформулируйте теорему, обратную признаку параллельности прямых, использующему соответственные углы. Дайте название полученной теореме и докажите ее.
Сформулируйте теорему, обратную признаку параллельности прямых, использующему односторонние углы. Дайте название полученной теореме и докажите ее.
Слайд 15
Задачи на готовых чертежах
с
а 4
2 3
b 1
1. Дано:
<1=75°, aǁb
Найти <2, <3, <4
c
a 2
4 3
5 1
b 6
2.Дано:
<1+<2=160°
aǁb
Найти: <3, <4, <5, <6.
Слайд 16
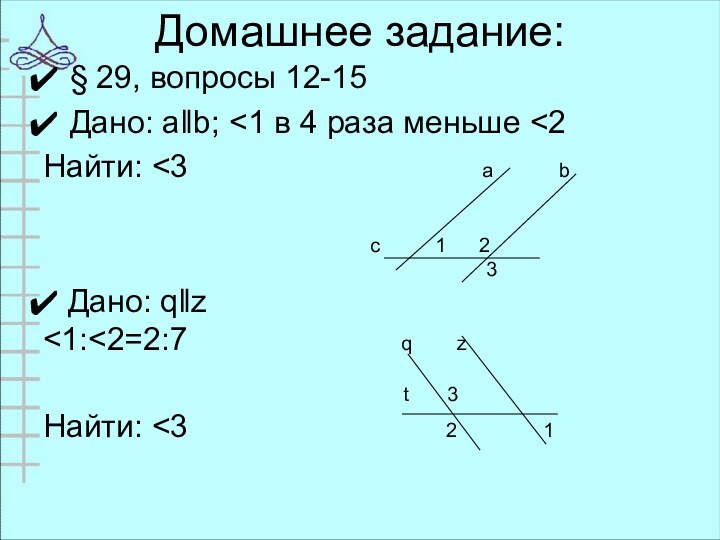
Домашнее задание:
§ 29, вопросы 12-15
Дано: aǁb;
4 раза меньше
a bc 1 2
3
Дано: qǁz
<1:<2=2:7 q z
t 3
Найти: <3 2 1