Презентация на тему Свойства равнобедренного треугольника

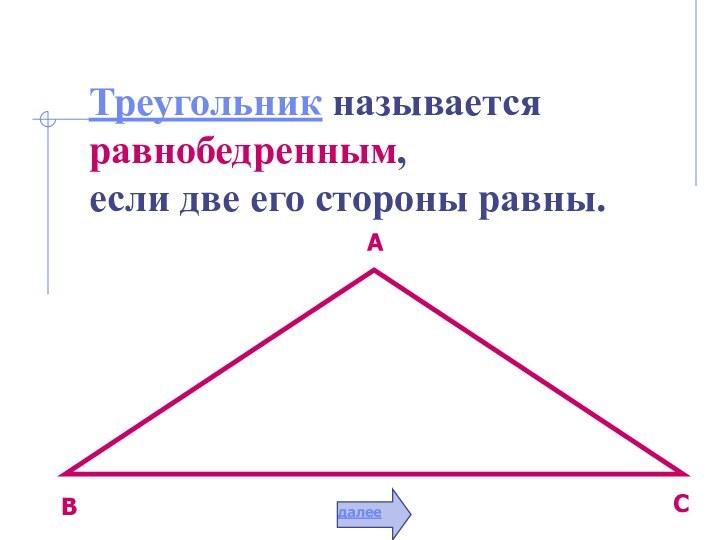
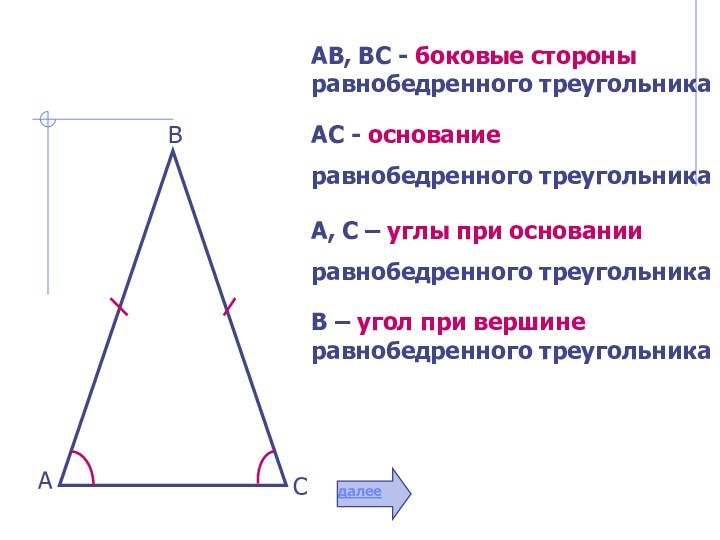
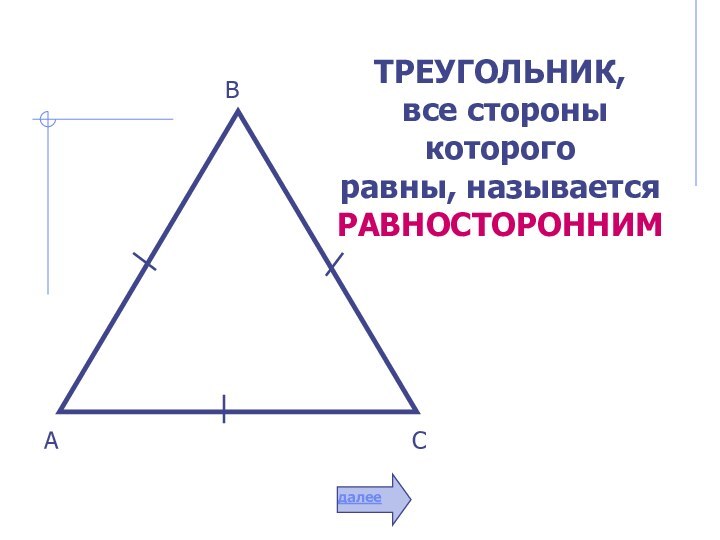
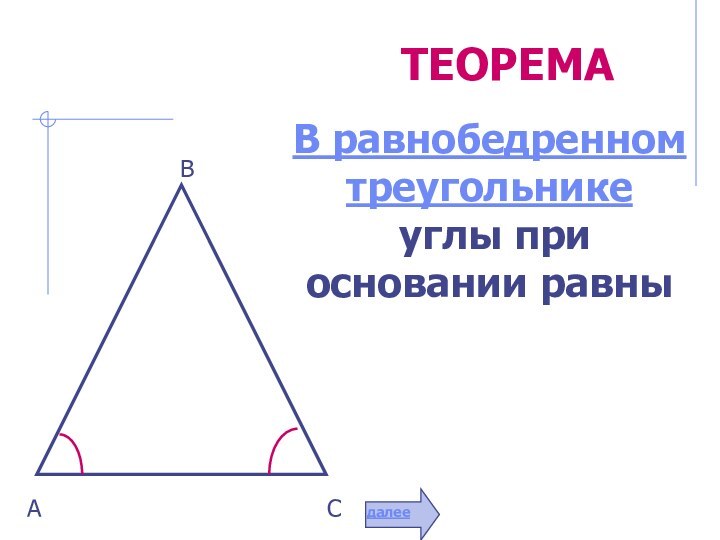
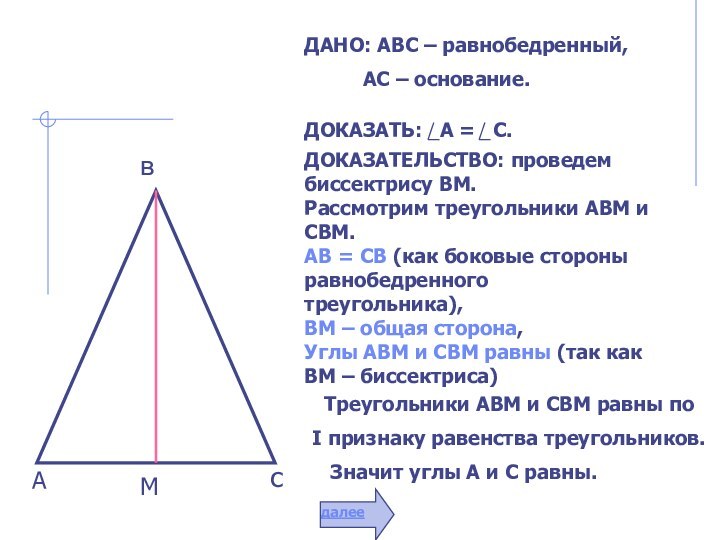
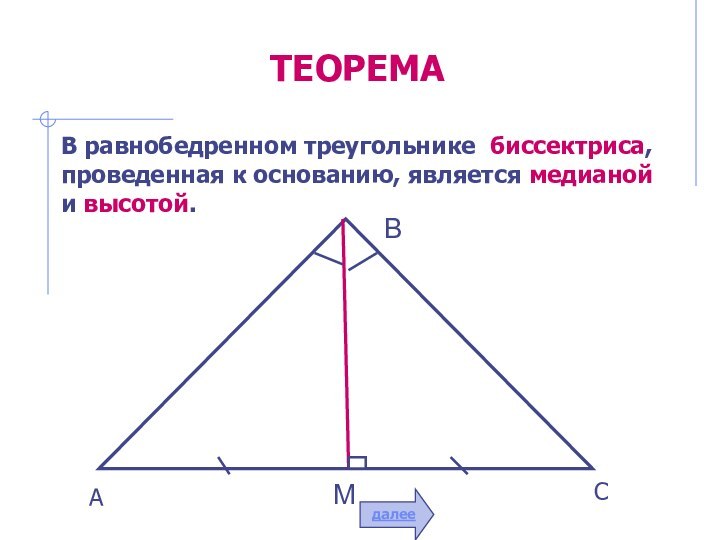
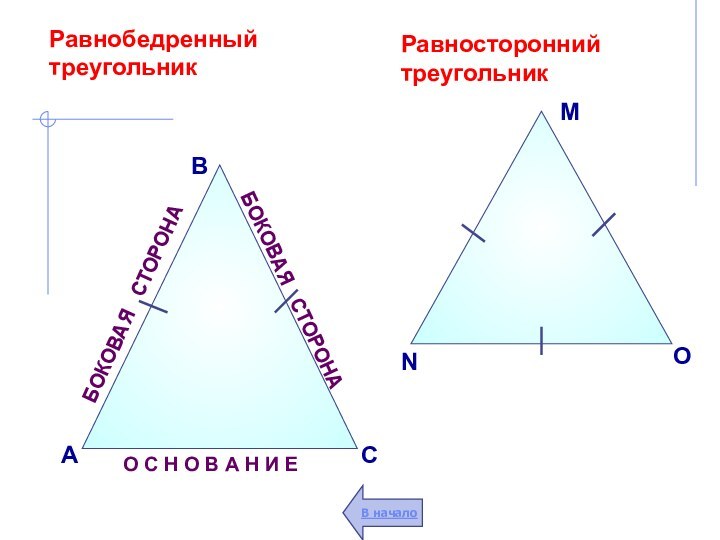
простая замкнутая
прямолинейная фигура.

Это одна из первых, свойства которой человек узнал еще в глубокой древности.
Эта фигура всегда имела широкое применение в практической жизни:
в строительном искусстве испокон веков используется свойство жесткости треугольника для укрепления различных строений и их деталей,
изображения треугольников и задачи на треугольники встречаются в папирусах, в старинных индийских книгах и в других древних документах.

далее

Историческая справка

Учение о треугольниках развивалось в ионийской школе,

основанной в VII в. до н. э. Фалесом, и в школе Пифагора.
Фалес доказал, что треугольник определяется одной стороной и двумя прилежащими к ней углами.
Учение о треугольниках было затем полностью изложено в первой книге “Начал” Евклида. Среди “определений ”, которыми начинается эта книга, имеются и следующие:
“Из трехсторонних фигур равносторонний треугольник есть фигура, имеющая три равные стороны.”
“Равнобедренный – фигура, имеющая только две равные стороны.”
“Разносторонний – фигура, имеющая три неравные стороны.”
Понятие о треугольнике исторически развивалось, по-видимому, так: сначала рассматривались лишь равносторонние, затем равнобедренные и, наконец, разносторонние треугольники.

к теме

Историческая справка

основание
равнобедренного треугольника
А, С – углы при основании
равнобедренного

треугольника

В – угол при вершине
равнобедренного треугольника

А

В

С

далее

обладает рядом геометрических свойств, которые привлекли к себе внимание

еще в древности. В задачах на треугольники, содержащихся в папирусе Ахмеса, на первый план выступают равнобедренный и прямоугольный треугольники.
На практике часто применялось свойство медианы равнобедренного треугольника, являющейся одновременно и высотой и биссектрисой. Термин “медиана” происходит от латинского слова mediana- “средняя” (линия). То, что углы при основании равнобедренного треугольника равны, было известно еще древним вавилонянам 4000 лет назад.

далее

Историческая справка

главного города Ионни, считается родоначальником греческой философии и науки.

Как философ, он учил, что явления мира не случайны, мир не хаотичен, а закономерен. Он считал, что вода есть начало всего. Из нее возникло все существующее и в нее в конце концов опять превращается.
Историческое значение философской деятельности Фалеса заключается в том, что им был сделан решающий шаг от мифологического мировоззрения к научному материалистическому представлению о мире.

далее

Историческая справка

Родоначальник греческой философии и науки

все философы Древней Греции тщательно занимались математикой, и в

частности, геометрией. Фалесу Милетскому Прокл приписывает открытие или доказательство теорем о том, что:
углы при основании равнобедренного треугольника равны,
диаметр делит круг пополам,
вертикальные углы равны и др.
Эти положения были частично известны еще вавилонянам и египтянам. Однако в отличие от вавилонской и египетской геометрии, имевшей преимущественно практический и прикладной характер, греческая геометрия характеризуется стремлением установить, что геометрические факты верны не только для отдельных частных случаев, а справедливы в любом случае.

далее

Историческая справка

Родоначальник греческой философии и науки

Открыл и доказал множество теорем

доказательств, с постепенным переходом от одной истины к другой,

греческие математики создали геометрию как науку. Направление строгой логической последовательности в геометрии первыми заложили геометры греческой ионнийской школы, основателем которой и был Фалес.

далее

Историческая справка

Родоначальник греческой философии и науки

Открыл и доказал множество теорем

Создатель геометрии как науки

ряд открытий в области астрономии: установил время равнодействий и

солнцестояний, определил продолжительность года, впервые наблюдал Малую Медведицу и и.п. Особенную славу ему принесло предсказание солнечного затмения, происшедшего в 585 г. до н. э. Фалес был не только философом и ученым, но также государственным и общественным деятелем. Вот почему он был причислен к группе “семи мудрецов” древности.

К теме

Историческая справка

Родоначальник греческой философии и науки

Открыл и доказал множество теорем

Создатель геометрии как науки

Сделал ряд открытий в астрономии

Причислен к группе “семи мудрецов” древности

АС – основание.
ДОКАЗАТЬ: А = С.
ДОКАЗАТЕЛЬСТВО:

проведем биссектрису ВМ.
Рассмотрим треугольники АВМ и СВМ.
АВ = СВ (как боковые стороны равнобедренного треугольника),
ВМ – общая сторона,
Углы АВМ и СВМ равны (так как ВМ – биссектриса)

Треугольники АВМ и СВМ равны по
I признаку равенства треугольников.
Значит углы А и С равны.

далее

медианой и высотой.
А
В
М
А
С
далее