Слайд 2
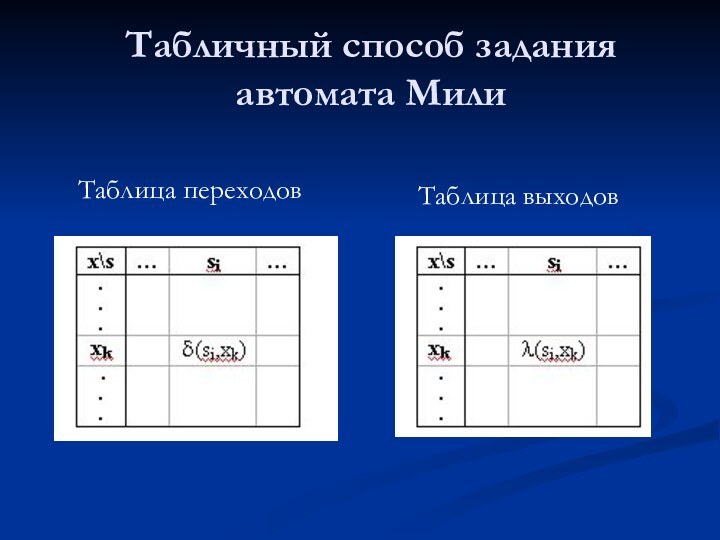
Табличный способ задания автомата Мили
Таблица выходов
Таблица переходов
Слайд 3
Графовый способ задания автомата Мили
Автомат представляется ориентированным графом
вершины графа соответствуют состояниям автомата, а дуги – переходам
из состояния в состояние.
каждая вершина помечается обозначением состояния
на каждой дуге указывается пометка вида: входных сигнал/выходной сигнал.
Слайд 4
Пример
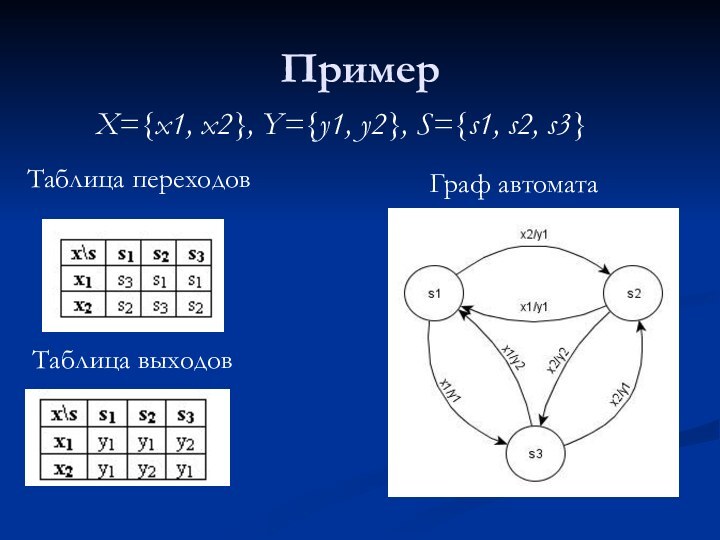
X={x1, x2}, Y={y1, y2}, S={s1, s2, s3}
Таблица переходов
Таблица
выходов
Граф автомата
Слайд 5
Пример автомата
X = {положительный стимул (1), отрицательный стимул
(0)}
Y = {есть реакция(1), нет реакции (0)}
S = {есть
реакция на последний положительный стимул (1), нет реакции на последний положительный стимул (0)}.
Функция λ: X×S →Y
0,0→0
0,1→0
1,0→1
1,1→0
Функция δ: X×S →S
0,0→0
0,1→1
1,0→1
1,1→0
Слайд 6
Пример
+
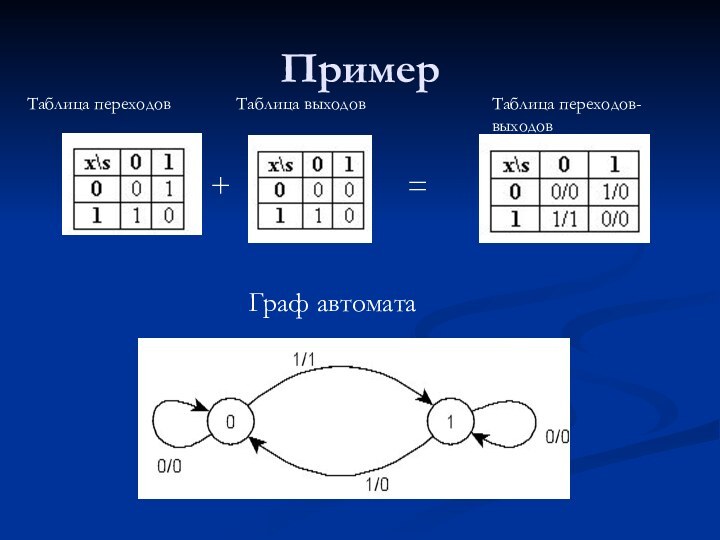
Таблица переходов
Таблица выходов
Таблица переходов- выходов
=
Граф автомата
Слайд 7
Табличный способ задания автомата Мура
Таблица переходов-выходов
Слайд 8
Графовый способ задания автомата Мура
Автомат представляется ориентированным графом
вершины графа соответствуют состояниям автомата, а дуги – переходам
из состояния в состояние.
каждая вершина помечается обозначением состояние/выходной сигнал
на каждой дуге указывается входных сигнал.
Слайд 9
Пример
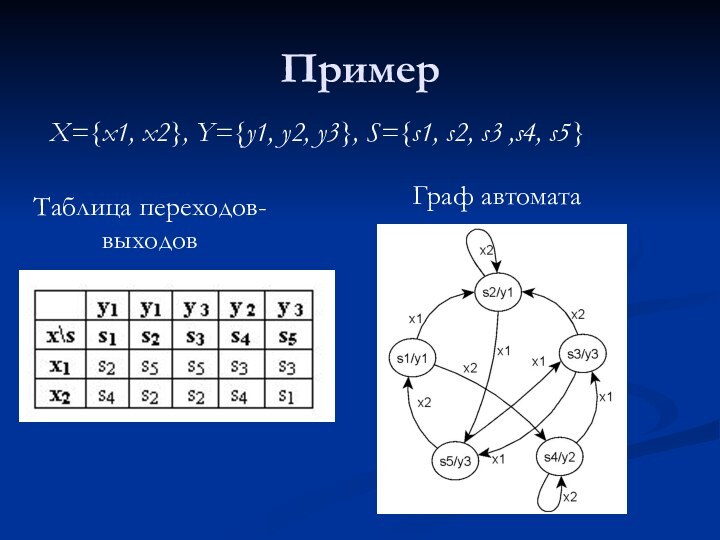
X={x1, x2}, Y={y1, y2, y3}, S={s1, s2, s3
,s4, s5}
Таблица переходов-выходов
Граф автомата
Слайд 10
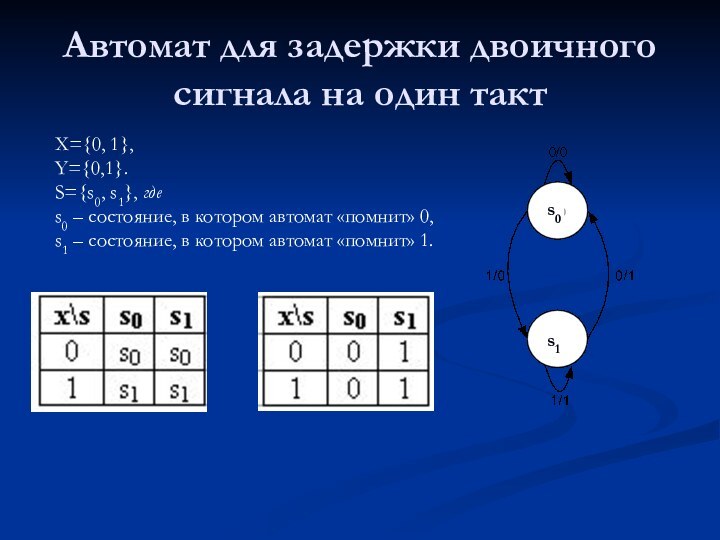
Автомат для задержки двоичного сигнала на один такт
X={0, 1},
Y={0,1}.
S={s0, s1}, где
s0 – состояние, в
котором автомат «помнит» 0,
s1 – состояние, в котором автомат «помнит» 1.
Слайд 11
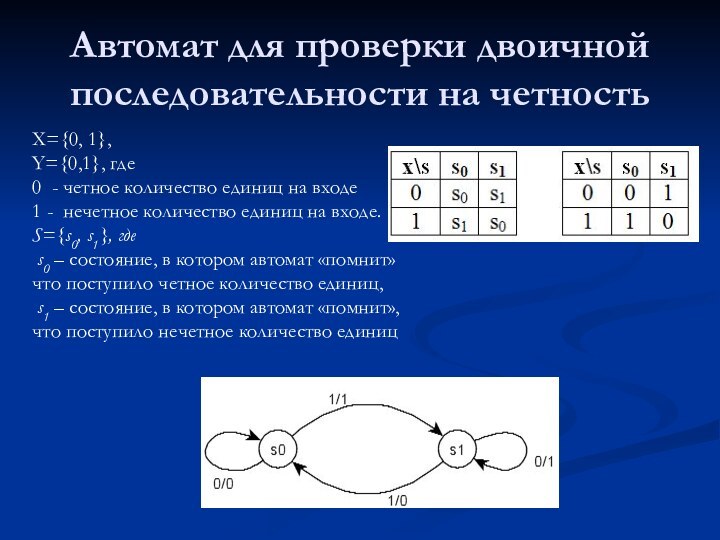
Автомат для проверки двоичной последовательности на четность
X={0,
1},
Y={0,1}, где
0 - четное количество единиц на входе
1
- нечетное количество единиц на входе.
S={s0, s1}, где
s0 – состояние, в котором автомат «помнит» что поступило четное количество единиц,
s1 – состояние, в котором автомат «помнит», что поступило нечетное количество единиц
Слайд 12
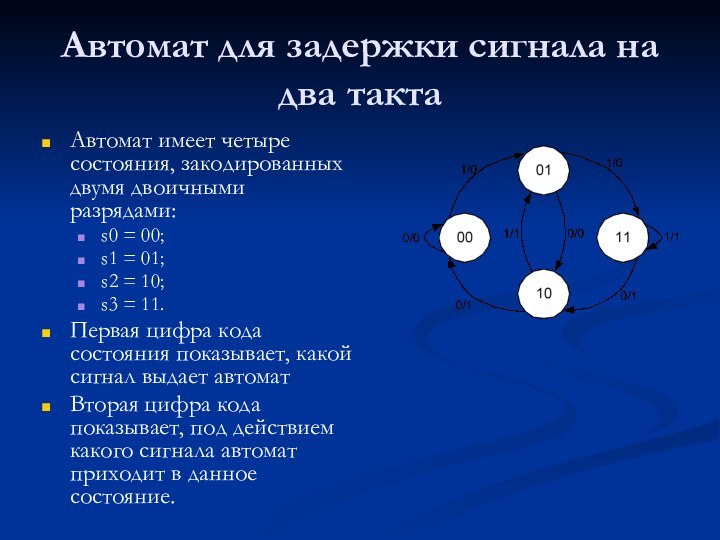
Автомат для задержки сигнала на два такта
Автомат имеет
четыре состояния, закодированных двумя двоичными разрядами:
s0 = 00;
s1
= 01;
s2 = 10;
s3 = 11.
Первая цифра кода состояния показывает, какой сигнал выдает автомат
Вторая цифра кода показывает, под действием какого сигнала автомат приходит в данное состояние.
Слайд 13
Конечный детерминированный автомат (КДА)
КДА – конечный автомат, в
котором имеется полная определенность переходов из всех состояний в
зависимости от входных сигналов
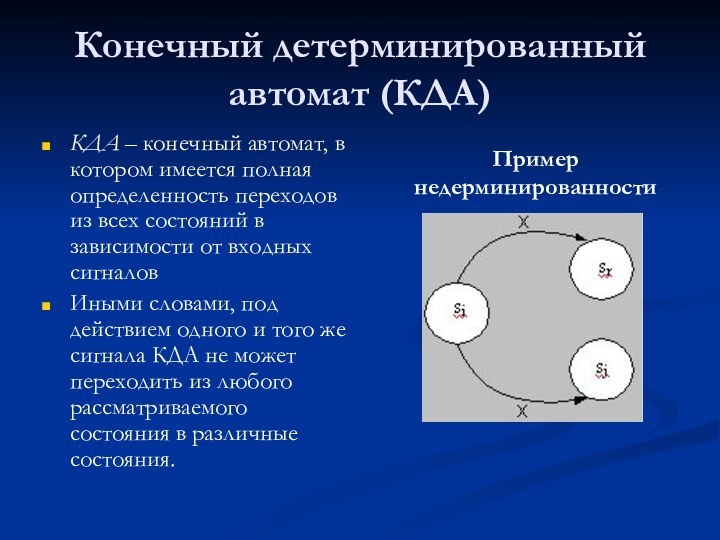
Иными словами, под действием одного и того же сигнала КДА не может переходить из любого рассматриваемого состояния в различные состояния.
Пример недерминированности
Слайд 14
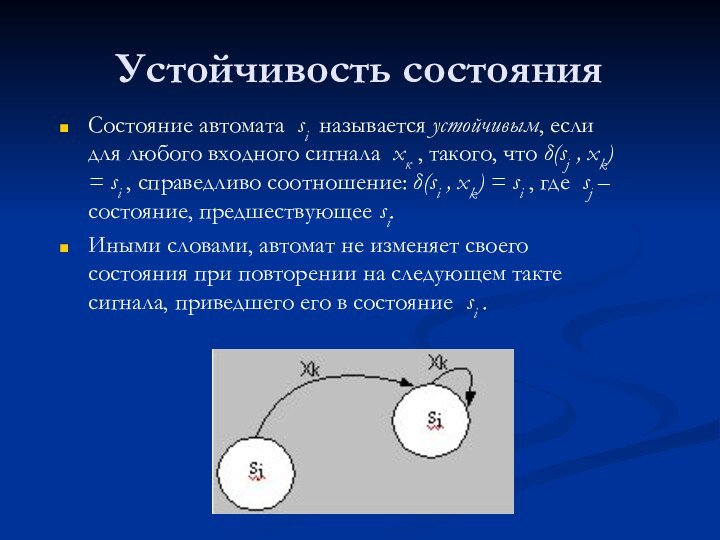
Устойчивость состояния
Состояние автомата si называется устойчивым, если для
любого входного сигнала хк , такого, что δ(sj ,
xk) = si , справедливо соотношение: δ(si , xk) = si , где sj – состояние, предшествующее si.
Иными словами, автомат не изменяет своего состояния при повторении на следующем такте сигнала, приведшего его в состояние si .
Слайд 15
Синхронные и асинхронные автоматы
Автомат называется асинхронным, если каждое
его состояние si ∈ S (i = 1, …
, n) устойчиво;
Устойчивость состояний в асинхронных автоматах достигается введением специальных сигналов синхронизации.
Если в автомате есть хотя бы одно неустойчивое состояние, он называется синхронным.
Слайд 16
Изолированный синхронный автомат
Изолированный (автономный) автомат – автомат, на
входе которого присутствует сигнал, имеющий постоянное значение, что эквивалентно
"отключению" входа.
Если изолированный КДА является синхронным, переходы из одного состояния в другое возможны, но при этом исключены разветвления путей.
Следовательно, изолированный КДА неизбежно должен попасть в состояние, в котором уже находился ранее, и на диаграммах переходов обязательно будет присутствовать поглощающее состояние или цикл.
Слайд 17
Примеры изолированного синхронного КДА
Длина цикла, измеренная числом дуг
на диаграмме, не превышает числа состояний,
Длина пути, перед
вхождение в цикл не превышает числа состояний.
Слайд 18
Проблема умножения
Теорема. Никакой конечный автомат не может перемножать
пары чисел с произвольно большим числом разрядов.
Доказательство.
Предположим
противное: существует автомат A, перемножающий пары двоичных чисел с произвольно большим числом разрядов (система счисления может быть любой без ограничения общности).
Используем для опровержения последнего утверждения частный случай: оба сомножителя равны 2n .
В этом случае каждый из сомножителей содержит единицу, за которой следуют n нулей;
Результат умножения (2n × 2n = 22n) содержит единицу и 2n нулей.
Слайд 19
Проблема умножения
Пусть пары разрядов сомножителей подаются последовательно, начиная
с младших разрядов
Чтобы автомат правильно работал, он должен
после прекращения подачи сомножителей
добавить к уже выработанным n + 1 нулям еще n – 1 нулей,
добавить в заключение единицу.
После прекращения подачи сомножителей автомат будет работать как изолированный.