- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Алгебра функций
Содержание
- 2. Конспект занятия. Учитель Винник Надежда Анатольевна
- 3. Понятие Функции f(х)x2x1xny1y2ynD(f)E(f)y=f(x)
- 4. Понятие ФункцииПусть D и Е – непустые
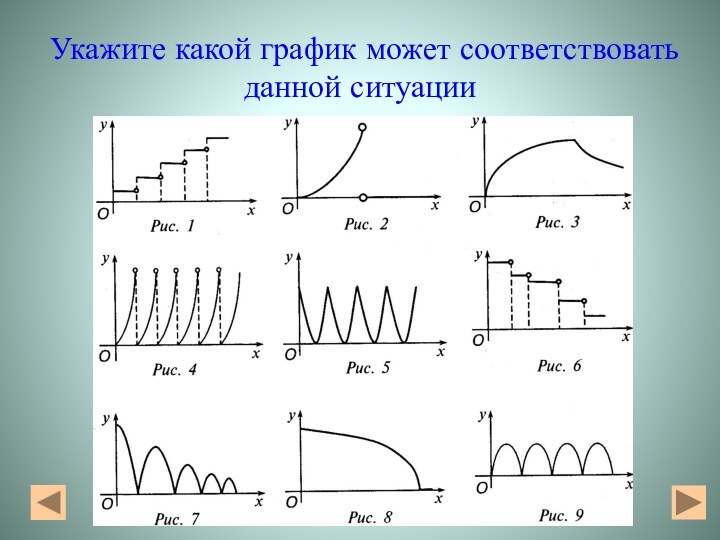
- 5. Определите какие графики соответствуют графикам функций
- 6. Укажите какой график может соответствовать данной ситуации
- 7. Укажите какой график может соответствовать данной ситуацииНа
- 8. Укажите какой график может соответствовать данной ситуации
- 9. Укажите какой график может соответствовать данной ситуации
- 10. Укажите какой график может соответствовать данной ситуации
- 11. Укажите какой график может соответствовать данной ситуации
- 12. Укажите какой график может соответствовать данной ситуации
- 13. Преобразование графиков функций. Симметричное отображение относительно
- 14. y = 2f(x)y = f(x) Преобразование графиков
- 15. y = 1/2f(x)y = f(x) Преобразование графиков
- 16. y = f(1/2х)y = f(x) Преобразование графиков
- 17. y = f(2х)y = f(x) Преобразование графиков
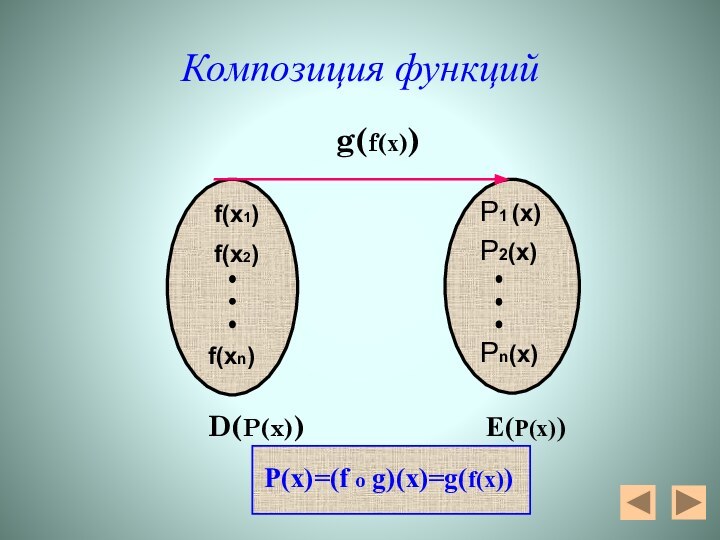
- 18. Композиция функций g(f(х))f(х2)f(х1)f(хn) P1 (x)P2(x)Pn(x)D(P(x)) P(x)=(f o g)(x)=g(f(x))E(P(x))
- 19. Композиция (суперпозиция или сложная функция)Определение: Пусть
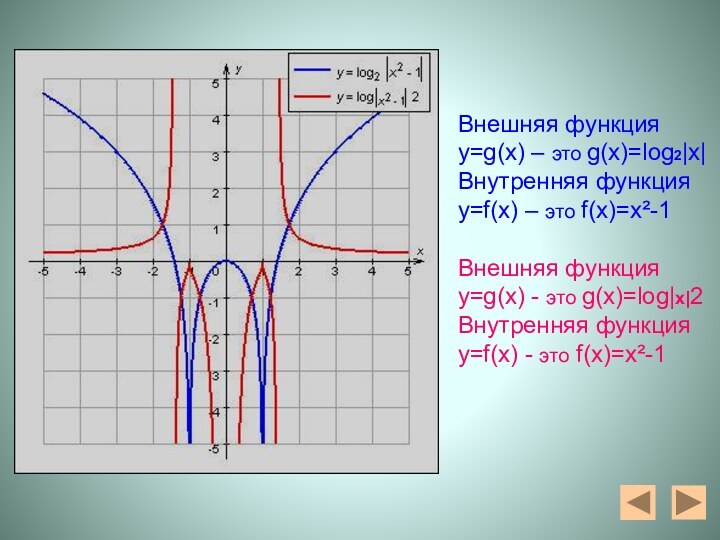
- 20. Внешняя функция y=g(x) – это g(x)=log2|x|Внутренняя
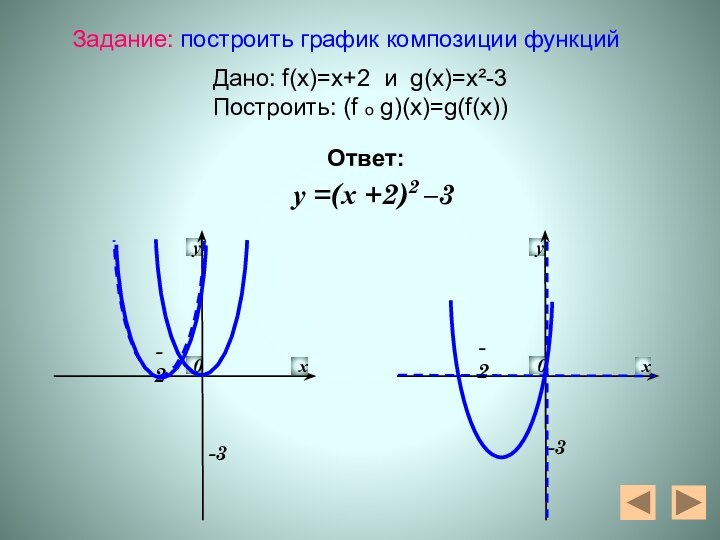
- 21. -3-2-3у =(х +2)2 –3 -2Задание: построить график
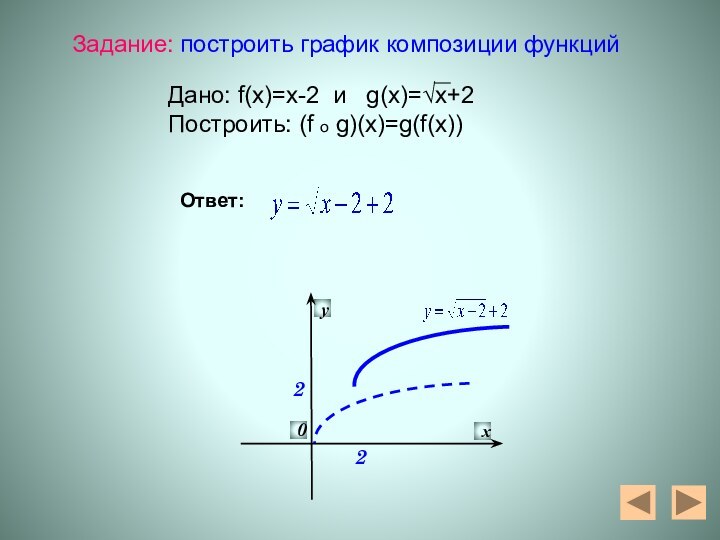
- 22. 22Задание: построить график композиции функцийДано: f(x)=x-2 и g(x)=√x+2Построить: (f o g)(x)=g(f(x))Ответ:
- 23. у =(х –3)3 – 43-4Задание: построить график
- 24. -3-2Задание: построить график композиции функцийДано: f(x)=x+3 и g(x)=1/x-2Построить: (f o g)(x)=g(f(x))Ответ:
- 25. y = x2 – 4 y =
- 26. у = (х –2)2 –1у = |(х
- 27. y = (x-1)2y = (|x|-1)20ухДано: f(x)=|х|-1 и
- 28. 0ухy = x2y = 2(x+2)2y = (x+2)2y
- 29. Домашнее задание №1 Пофантазируйте!
- 30. Домашнее задание №2 Составьте композицию из двух функций и постройте её график
- 31. Как вы оцениваете свою работу на
- 32. До свидания!Всем спасибо!
- 33. Скачать презентацию
- 34. Похожие презентации












Слайд 4
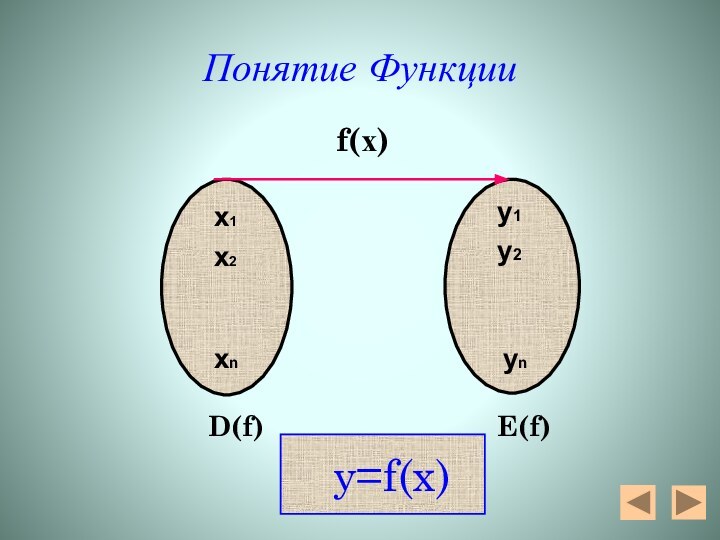
Понятие Функции
Пусть D и Е – непустые числовые
множества,
а Х и У – соответственно их элементы. Если каждому Х є D (Х принадлежит множеству D) ставится, в соответствии с некоторым законом, только одно значение У є Е, то говорят, что между переменными Х и У существует функциональная зависимость, и Х называют независимой переменной (или аргументом), а У – зависимой переменной ( или функцией).Термин «функция» ввёл в математику Готфрид Лейбниц (1646-1716 гг.)- он употреблял его, связывая только с геометрическими образами.
В развитие понятия функции внесли свой вклад Исаак Ньютон (1643-1727 гг.), Леонард Эйлер (1707-1783 гг.), Ж.-Б. Фурье (1768-1830гг.), Н.И. Лобачевский (1792-1856гг.), Дирихле (1805-1859гг.)
Слайд 7
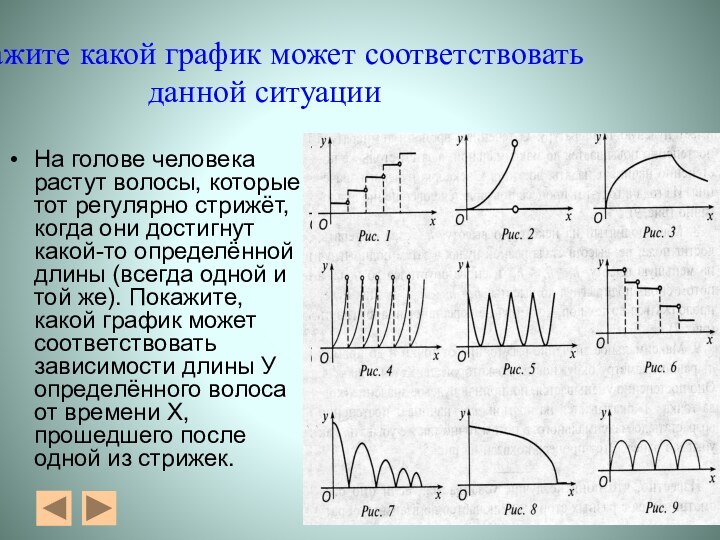
Укажите какой график может соответствовать данной ситуации
На голове
человека растут волосы, которые тот регулярно стрижёт, когда они
достигнут какой-то определённой длины (всегда одной и той же). Покажите, какой график может соответствовать зависимости длины У определённого волоса от времени Х, прошедшего после одной из стрижек.
Слайд 8
Укажите какой график может соответствовать данной ситуации
Конус
погружают в воду вниз вершиной. Как зависит У –
масса вытесненной воды – от величины Х, выражающей глубину погружения? Найдите соответствующий график.
Слайд 9
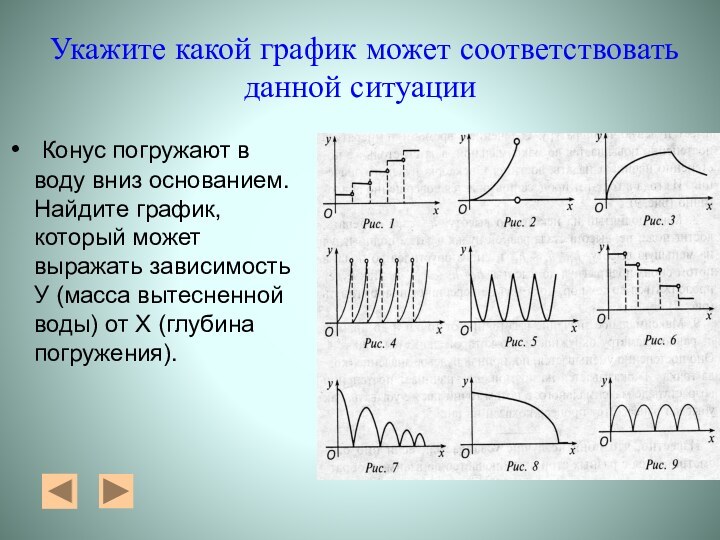
Укажите какой график может соответствовать данной ситуации
Конус
погружают в воду вниз основанием. Найдите график, который может
выражать зависимость У (масса вытесненной воды) от Х (глубина погружения).
Слайд 10
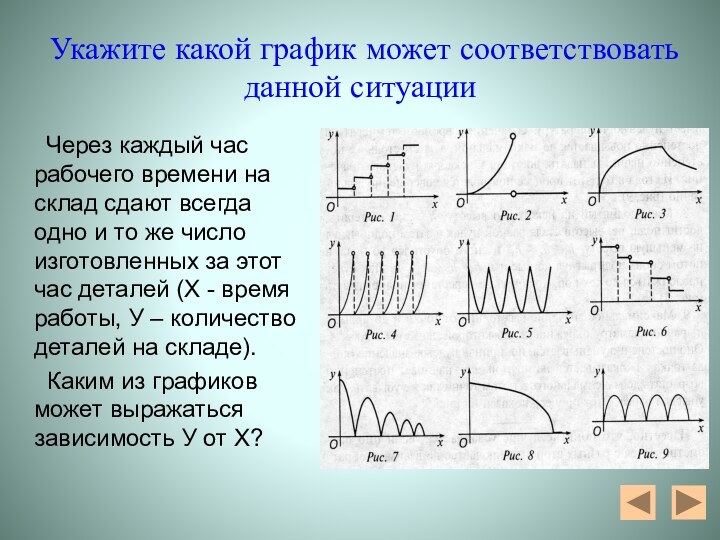
Укажите какой график может соответствовать данной ситуации
Через каждый час рабочего времени на склад сдают
всегда одно и то же число изготовленных за этот час деталей (Х - время работы, У – количество деталей на складе).Каким из графиков может выражаться зависимость У от Х?
Слайд 11
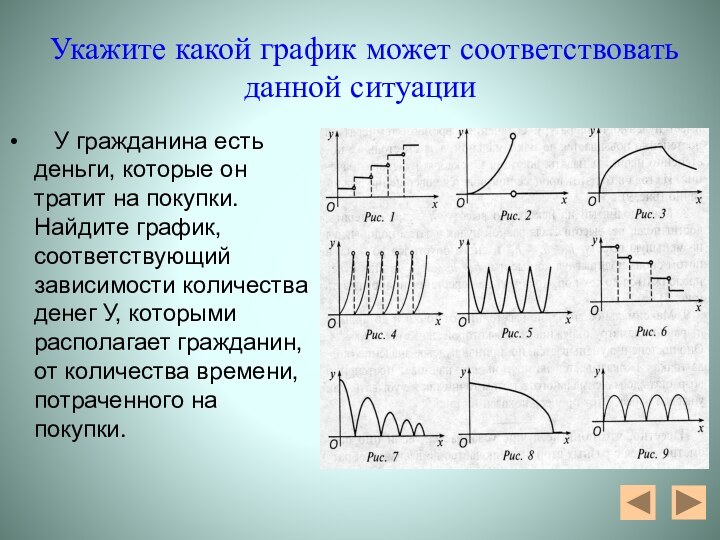
Укажите какой график может соответствовать данной ситуации
У гражданина есть деньги, которые он тратит на покупки.
Найдите график, соответствующий зависимости количества денег У, которыми располагает гражданин, от количества времени, потраченного на покупки.
Слайд 12
Укажите какой график может соответствовать данной ситуации
Яблоко
растёт, затем его срывают и сушат. На весь этот
процесс уходит Х дней. Найдите график, описывающий зависимость массы яблока У от Х.
Слайд 13
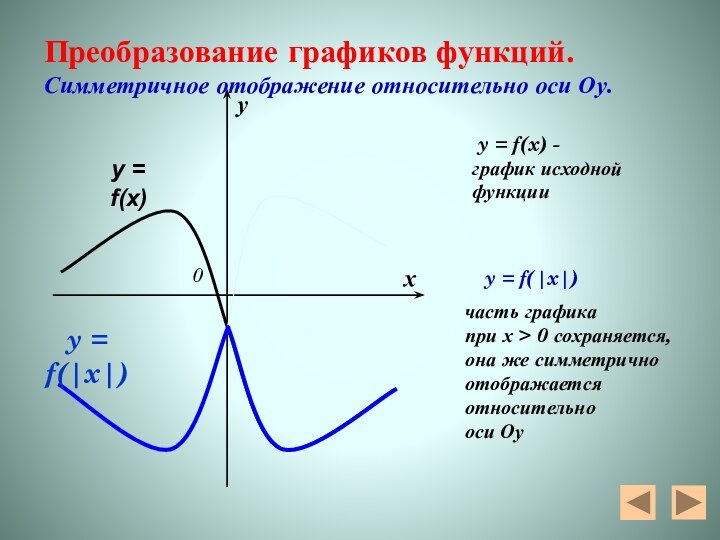
Преобразование графиков функций.
Симметричное отображение относительно оси Оу.
y = f(x) -
график исходной
функции
y = f(|x|)
часть графика
при х > 0 сохраняется,
она же симметрично
отображается
относительно
оси Оу
х
у
0
y = f(x)
y = f(|x|)
Слайд 14
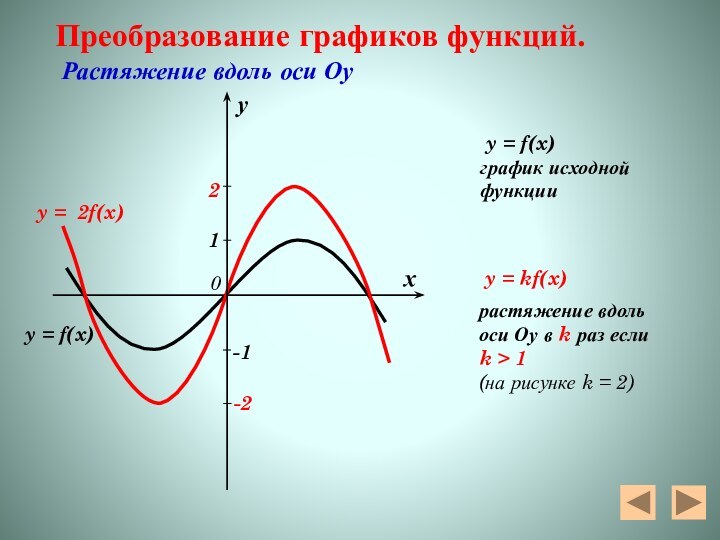
y = 2f(x)
y = f(x)
Преобразование графиков функций.
Растяжение вдоль оси Оу
y = f(x)
график исходнойфункции
y = kf(x)
растяжение вдоль
оси Оу в k раз если
k > 1
(на рисунке k = 2)
х
у
0
2
-2
-1
1
Слайд 15
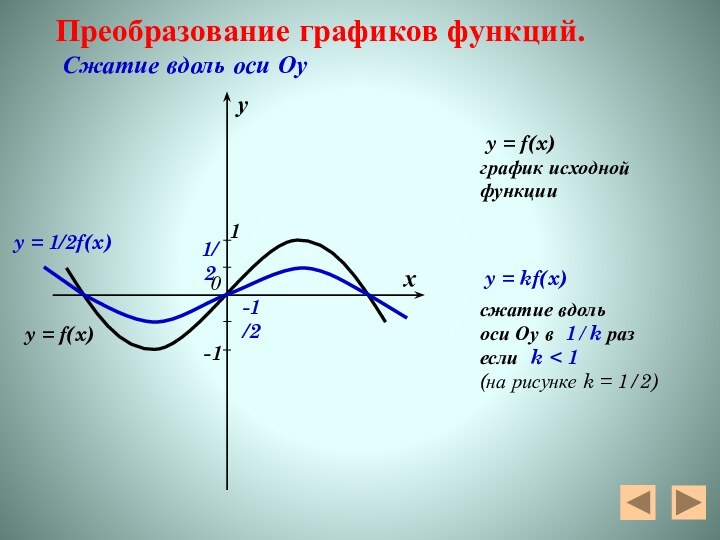
y = 1/2f(x)
y = f(x)
Преобразование графиков функций.
Сжатие вдоль оси Оу
y = f(x)
график исходнойфункции
y = kf(x)
сжатие вдоль
оси Оу в 1/k раз
если k < 1
(на рисунке k = 1/2)
х
у
0
1/2
-1/2
1
-1
Слайд 16
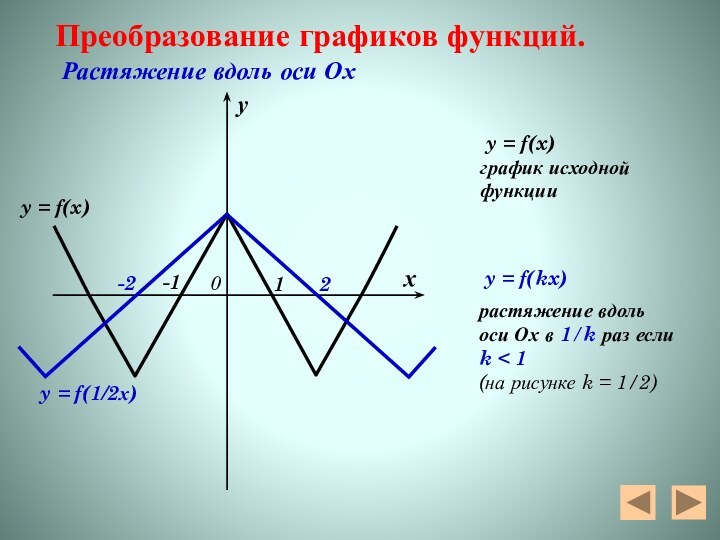
y = f(1/2х)
y = f(x)
Преобразование графиков функций.
Растяжение вдоль оси Ох
y = f(x)
график исходнойфункции
y = f(kx)
растяжение вдоль
оси Ох в 1/k раз если
k < 1
(на рисунке k = 1/2)
х
у
0
2
-2
-1
1
Слайд 17
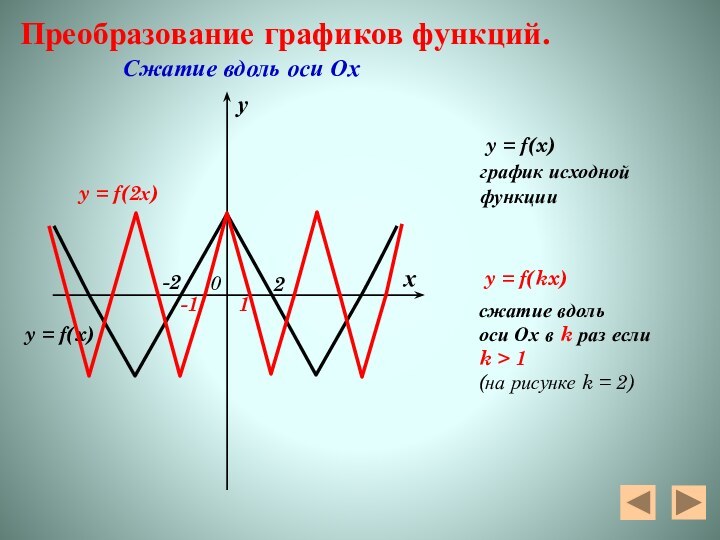
y = f(2х)
y = f(x)
Преобразование графиков функций.
Сжатие
вдоль оси Ох y = f(x)
график исходной
функции
y = f(kx)
сжатие вдоль
оси Ох в k раз если
k > 1
(на рисунке k = 2)
х
у
0
1
-1
-2
2
Слайд 18
Композиция функций
g(f(х))
f(х2)
f(х1)
f(хn)
P1 (x)
P2(x)
Pn(x)
D(P(x))
P(x)=(f o g)(x)=g(f(x))
E(P(x))
Слайд 19
Композиция (суперпозиция или сложная функция)
Определение:
Пусть даны
две функции у=g(x) и y=f(x),
их композицией называют функциюP(x)=(f o g)(x)=g(f(x)), при условии Д(f)∩E(g)≠Ø
g(x)-внешняя функция
f(x)- внутренняя функция
В функцию g(x) надо вместо х подставить функциюf(x)
Композиция не коммутативна
(g o f) ≠ (f o g)
Слайд 20
Внешняя функция y=g(x) – это g(x)=log2|x|
Внутренняя функция
у=f(x) – это f(x)=x²-1
Внешняя функция y=g(x) - это g(x)=log|х|2
Внутренняя
функцияу=f(x) - это f(x)=x²-1
Слайд 21
-3
-2
-3
у =(х +2)2 –3
-2
Задание: построить график композиции
функций
Дано: f(x)=x+2 и g(x)=x²-3
Построить: (f o g)(x)=g(f(x))Ответ:
Слайд 22
2
2
Задание: построить график композиции функций
Дано: f(x)=x-2 и
g(x)=√x+2
Построить: (f o g)(x)=g(f(x))
Ответ:
Слайд 23
у =(х –3)3 – 4
3
-4
Задание: построить график
композиции
функций
Дано: f(x)=x-3 и g(x)=x³-4
Построить: (f o g)(x)=g(f(x))
Ответ:
у =(х
–3)³ – 4х³
Слайд 24
-3
-2
Задание: построить график композиции функций
Дано: f(x)=x+3 и
g(x)=1/x-2
Построить: (f o g)(x)=g(f(x))
Ответ:
Слайд 25
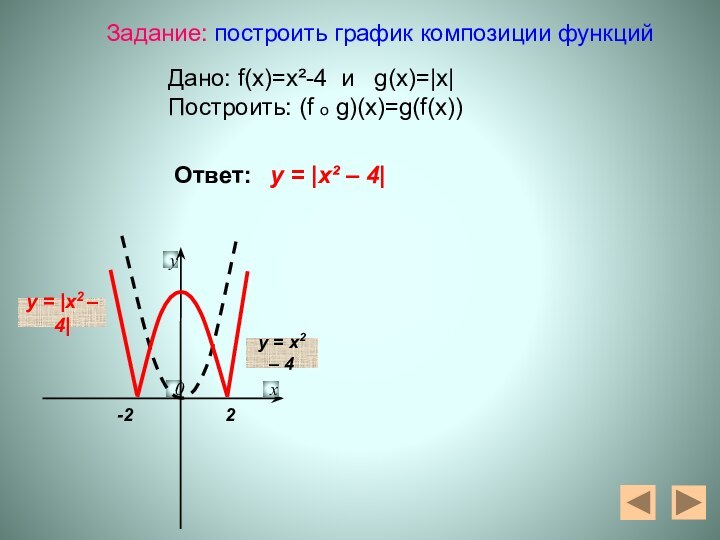
y = x2 – 4
y = |x2
– 4|
Задание: построить график композиции функций
Дано: f(x)=x²-4 и
g(x)=|x|Построить: (f o g)(x)=g(f(x))
Ответ:
y = |x² – 4|
-2
2
Слайд 26
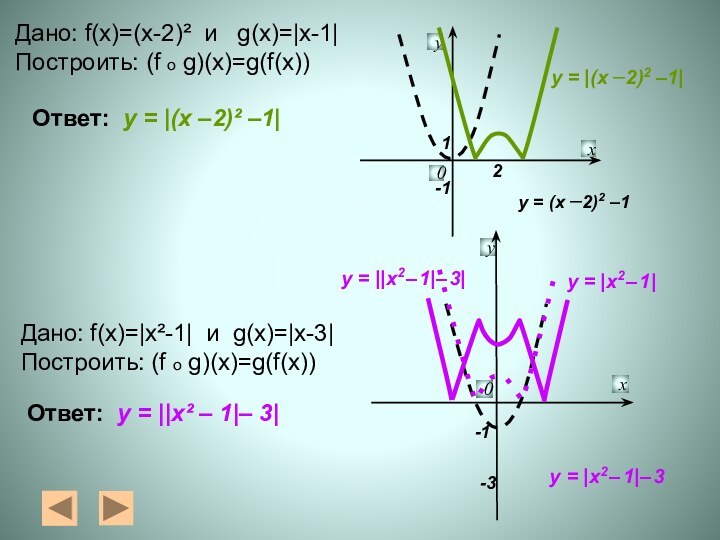
у = (х –2)2 –1
у = |(х –2)2
–1|
у = |х2 – 1|
у
= |х2 – 1|– 3 у = ||х2 – 1|– 3|
Дано: f(x)=(x-2)² и g(x)=|x-1|
Построить: (f o g)(x)=g(f(x))
Дано: f(x)=|х²-1| и g(x)=|х-3|
Построить: (f o g)(x)=g(f(x))
Ответ:
Ответ:
у = |(х –2)² –1|
у = ||х² – 1|– 3|
2
-1
-3
-1
1
Слайд 27
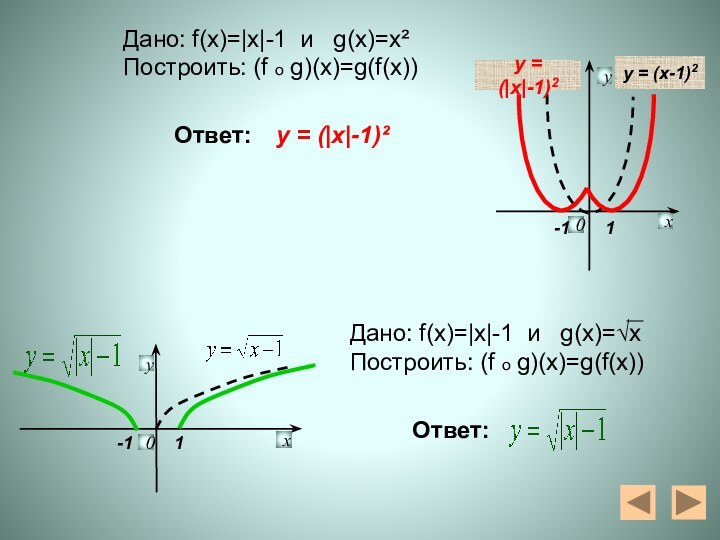
y = (x-1)2
y = (|x|-1)2
0
у
х
Дано: f(x)=|х|-1 и
g(x)=х²
Построить: (f o g)(x)=g(f(x))
Дано: f(x)=|х|-1 и g(x)=√x
Построить: (f
o g)(x)=g(f(x))Ответ:
Ответ:
y = (|x|-1)²
-1
1
-1
1
Слайд 28
0
у
х
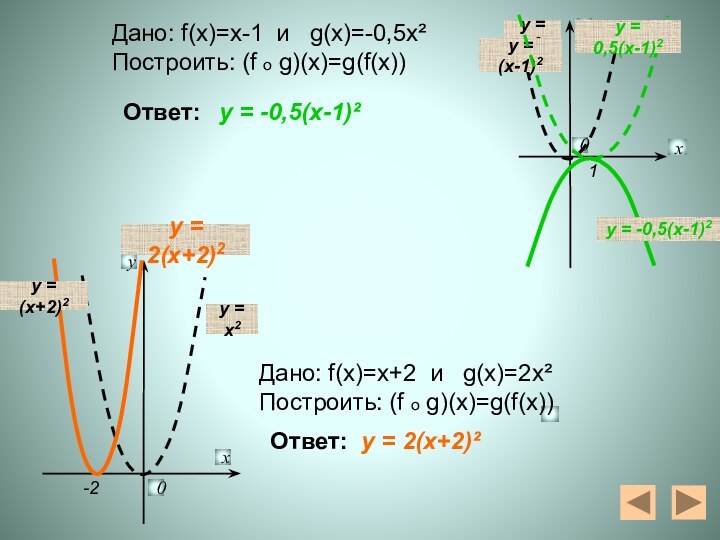
y = x2
y = 2(x+2)2
y = (x+2)2
y =
x2
y = (x-1)2
y = 0,5(x-1)2
y = -0,5(x-1)2
Дано: f(x)=х-1 и
g(x)=-0,5х²Построить: (f o g)(x)=g(f(x))
Дано: f(x)=х+2 и g(x)=2х²
Построить: (f o g)(x)=g(f(x))
Ответ:
Ответ:
y = -0,5(x-1)²
y = 2(x+2)²
1
-2
Слайд 29
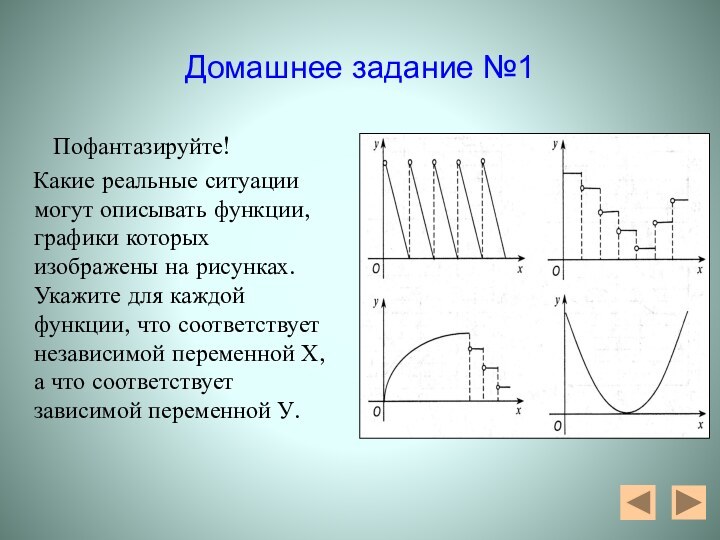
Домашнее задание №1
Пофантазируйте!
Какие реальные ситуации могут описывать функции, графики которых
изображены на рисунках. Укажите для каждой функции, что соответствует независимой переменной Х, а что соответствует зависимой переменной У.
Слайд 31
Как вы оцениваете свою работу на уроке?
Какие задания оказались
для вас трудными?
Какие задания показались
вам лёгкими?Что бы вы хотели пожелать, в том числе и предложения по разработке последующих занятий?