- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Теорема Пифагора 8 класс
Содержание
- 2. Теорема Пифагора Цели: познакомить учащихся
- 3. ПЛАН1. Повторение2. Историческая справка3.Доказательство теоремы Пифагора4. Решение задач (по готовым чертежам)5. Старинная задача
- 4. Чему равна сумма квадратов чисел?а) 32+42 =
- 5. Верно ли решение? 32+42=(3+4)2нет
- 6. Чему равно? (а+в)2=а2+2ав+в2
- 7. Какой треугольник изображен на рисунке? Равнобедренный
- 8. Какой треугольник изображен на рисунке?Равностороннийааа
- 9. Какой треугольник изображен на рисунке? ПрямоугольныйС
- 10. Как называются стороны этого треугольника?а, в – катеты,с - гипотенуза Ссав
- 11. Найдите площадь треугольника S= (6*8)=24А СВ68
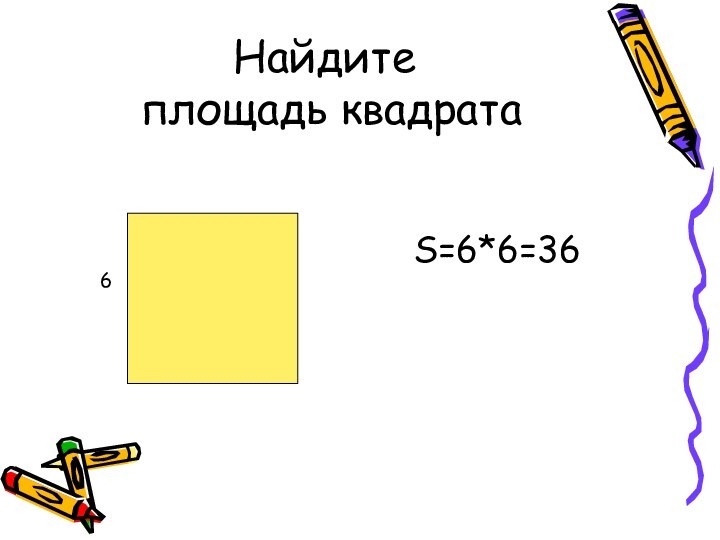
- 12. Найдите площадь квадрата S=6*6=366
- 13. 1.Начертить прямоугольный треугольник. 2. На сторонах треугольника построим квадраты.Практическая работа.
- 14. 1. Найдите площадь каждого
- 15. Вывод: Площадь квадрата построенного на гипотенузе прямоугольного треугольника равна сумме площадей квадратов, построенных на катетах.
- 16. Теорема Пифагора во времена Пифагора теорема была
- 17. Теорема Пифагора современная формулировка:«Квадрат гипотенузы равен сумме
- 18. Начертим прямоугольный треугольник
- 19. С другой стороныSABCD=4Sтр +SквSтр= ав; Sкв=c2SABCD=4* ав+с2=2ав+с2(а+в)2=2ав+с2а2+2ав+в2=2ав+с2а2+в2=с2ч.т.д.авсАВСDааавввсссcccc
- 20. Решение задач Составьте по рисунку, используя теорему
- 21. Можно ли применять теорему Пифагора
- 22. Итак, вопрос: На что надо обратить
- 23. Старинная задача«На берегу реки рос тополь одинокийВдруг
- 24. Дано: АСД, А=900
- 25. Домашнее задание Пункт 54. №483 (б), №484 (в)
- 26. Скачать презентацию
- 27. Похожие презентации
Теорема Пифагора Цели: познакомить учащихся с жизнью ученого Пифагора, изложить теорему Пифагора, отработать ее на простых задачах; познакомить учащихся со старинной задачей




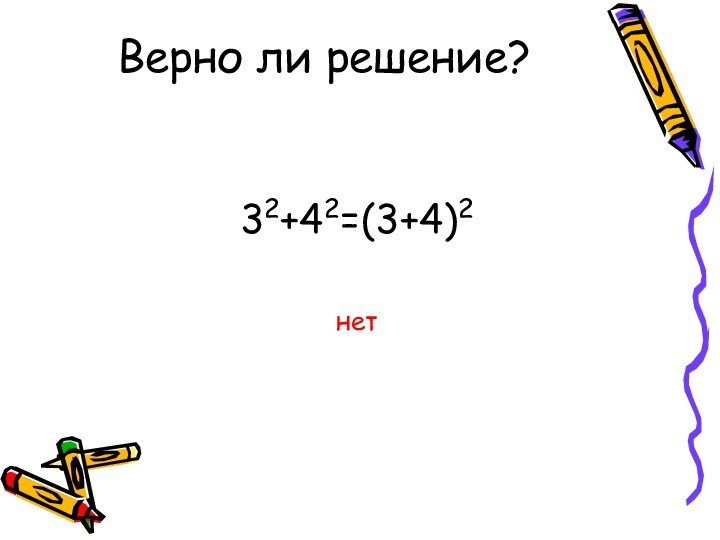
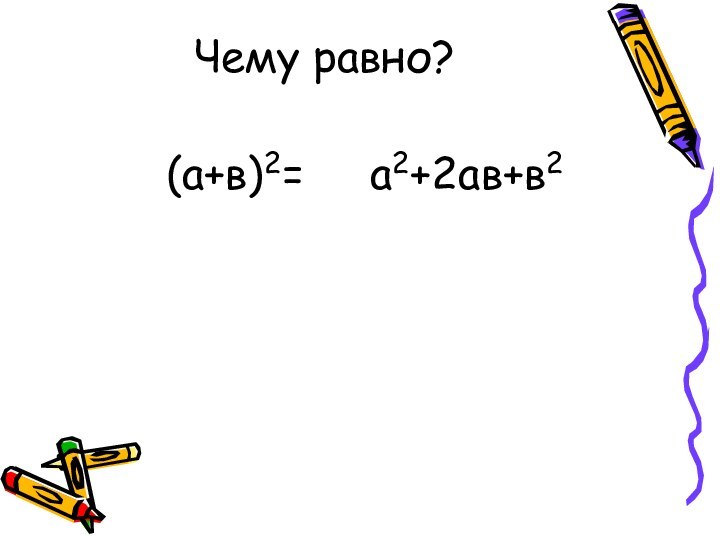















Слайд 3
ПЛАН
1. Повторение
2. Историческая справка
3.Доказательство теоремы Пифагора
4. Решение задач
(по готовым чертежам)
5. Старинная задача
Слайд 13
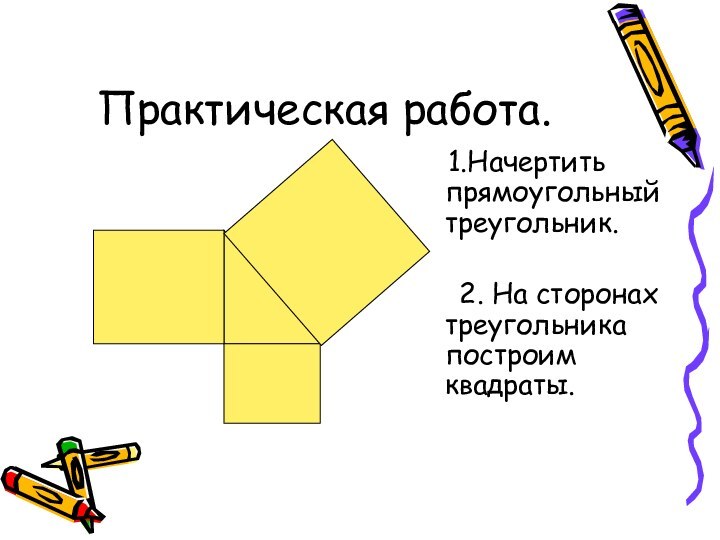
1.Начертить прямоугольный треугольник.
2. На сторонах треугольника построим квадраты.
Практическая работа.
Слайд 14
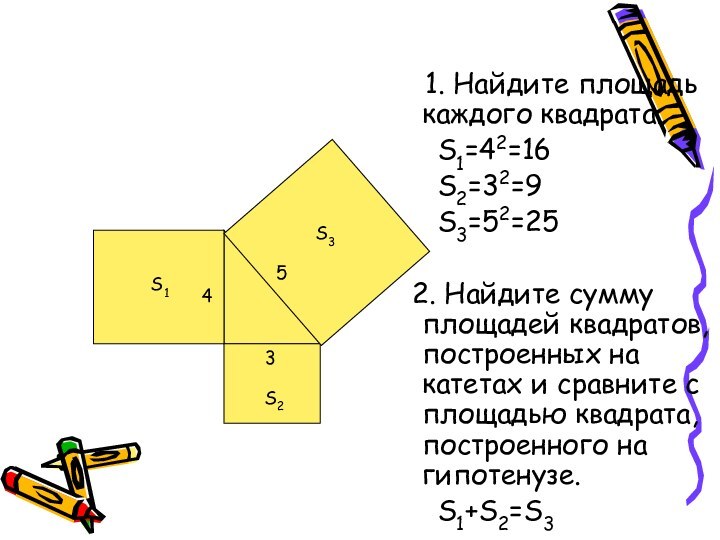
1. Найдите площадь каждого квадрата.
S1=42=16
S2=32=9
S3=52=252. Найдите сумму площадей квадратов, построенных на катетах и сравните с площадью квадрата, построенного на гипотенузе.
S1+S2=S3
4
3
5
S1
S3
S2
Слайд 15
Вывод:
Площадь квадрата построенного на гипотенузе прямоугольного
треугольника равна сумме площадей квадратов, построенных на катетах.
Слайд 16
Теорема Пифагора
во времена Пифагора теорема была сформулирована так:
«Доказать, что квадрат, построенный на гипотенузе прямоугольного треугольника, равновелик
сумме квадратов, построенных на катетах»
Слайд 17
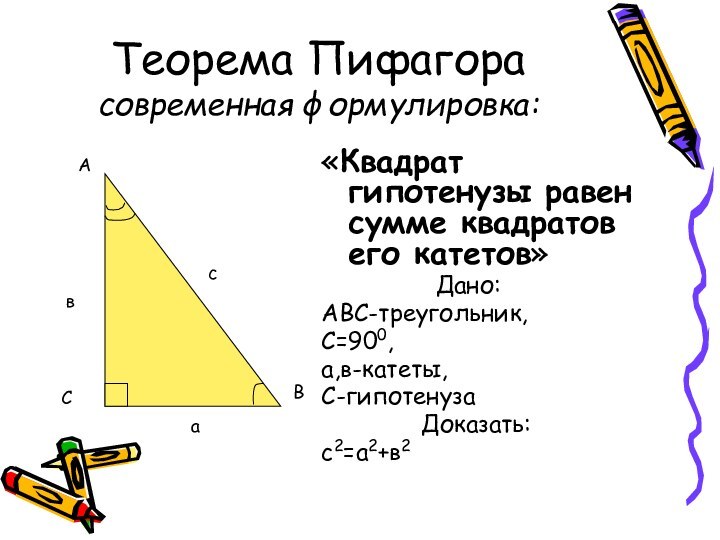
Теорема Пифагора
современная формулировка:
«Квадрат гипотенузы равен сумме квадратов его
катетов»
Дано:
АВС-треугольник,
С=900,
а,в-катеты,
С-гипотенуза
Доказать:
с2=а2+в2
А
В
С
с
а
в
Слайд 18
Начертим прямоугольный треугольник со
сторонами а, в, с.
Достроим треугольник до
квадрата со сторонами а+в.Найдем площадь этого квадрата
S=(а + в)2
а
с
в
в
в
в
а
а
а
Доказательство:
Слайд 19
С другой стороны
SABCD=4Sтр +Sкв
Sтр= ав;
Sкв=c2
SABCD=4*
ав+с2=2ав+с2
(а+в)2=2ав+с2
а2+2ав+в2=2ав+с2
а2+в2=с2
ч.т.д.
а
в
с
А
В
С
D
а
а
а
в
в
в
с
с
с
c
c
c
c
Слайд 20
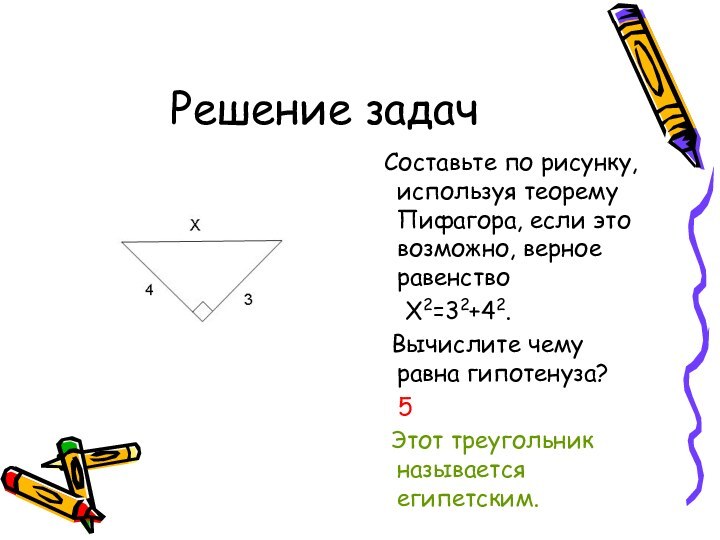
Решение задач
Составьте по рисунку, используя теорему Пифагора,
если это возможно, верное равенство
Х2=32+42.
Вычислите чему равна гипотенуза?5
Этот треугольник называется египетским.
Слайд 21
Можно ли применять теорему Пифагора к
этому треугольнику?
Нет. Так как этот треугольник не
прямоугольный
Слайд 22
Итак, вопрос:
На что надо обратить внимание
при применении теоремы Пифагора?
Чтобы использовать теорему Пифагора,
надо убедиться, что треугольник прямоугольный.
Слайд 23
Старинная задача
«На берегу реки рос тополь одинокий
Вдруг ветра
порыв его ствол надломал.
Бедный тополь упал. И угол прямой
С течением реки его ствол составлял.
Запомни теперь, что в том месте река
В четыре лишь фута была широка.
Верхушка склонилась у края реки
Осталось три фута всего от ствола,
Прошу тебя, скоро теперь мне скажи:
У тополя как велика высота?»
Слайд 24
Дано: АСД, А=900
АС=3 фута, АD=4 фута.
Найти: АВ.
Решение
АВ=АС+СD.
По
теореме ПифагораCD2=AC2+CD2, СD2= 9+16
CD2=25, СD=5.
АВ=3 +5 =8(футов).
Ответ: 8 футов.