Презентация на тему Треугольник простейший и неисчерпаемый

тругольников по отношению к сторонам
Признаки равенства треугольников
Равнобедренный треугольник
Сумма углов

треугольника

Свойство внешнего угла треугольника

Теорема Пифагора

Площадь треугольника

Тест

точки А, В и С; стороны – отрезки a=ВС,

b=АС и c=АВ, соединяющие вершины; углы, образованные тремя парами сторон. Углы часто обозначают так же, как и вершины – буквами А, В и С. Кроме этих основных элементов в треугольнике рассматривают и другие отрезки, обладающие интересными свойствами, прежде всего средние линии, медианы, биссектрисы и высоты.

МЕНЮ

сторон. Три средние линии треугольника образуют «вписанный» в него

треугольник, называемый серединным.

А

В

С

Средние
линии

МЕНЮ

соединяющие вершины треугольника с серединами противоположных сторон.
А
В
С
Медианы
МЕНЮ

– «рассекаю») называют заключенные внутри треугольника отрезки прямых, которые

делят пополам его углы.

А

В

С

Биссектрисы

МЕНЮ

прямой, содержащей противоположную сторону.
А
В
С
Высоты
А
В
С
Высоты
МЕНЮ
А
В
С
Высоты

основное свойство равнобедренного треугольника: углы при его основании равны.
Доказательство

этой теоремы приписывают Фалесу Милетскому, жившему за два века до Евклида. Впоследствии теорема получила название Pons asinorum, что на латыни означает «мост ослов». Объясняют такое название, с одной стороны, тем, что чертеж, использованный Евклидом для ее доказательства, напоминает мостик, а с другой – мнением, будто только ослы не могут этот мостик перейти. (Впрочем, в современном английском языке латинское выражение «pons asinorum» употребляется в несколько ином смысле – как «суровое испытание способностей неопытного человека».)

Равнобедренный треугольник

МЕНЮ

треугольника используют его симметричность. Треугольник можно перевернуть и наложить

на себя так, что каждая из боковых сторон совпадет с другой; тогда и углы при основании совместятся друг с другом.

МЕНЮ

В

С

Если углы при основании треугольника равны, то он равнобедренный.

1

2

3

4

Верна и обратная теорема:

А

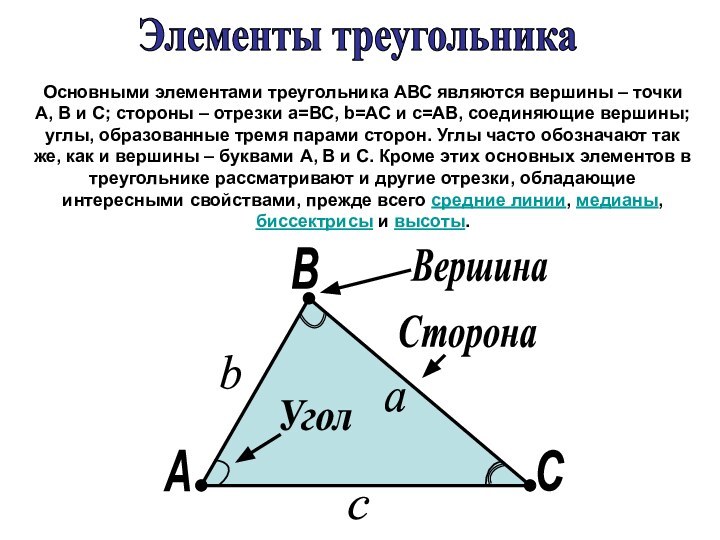
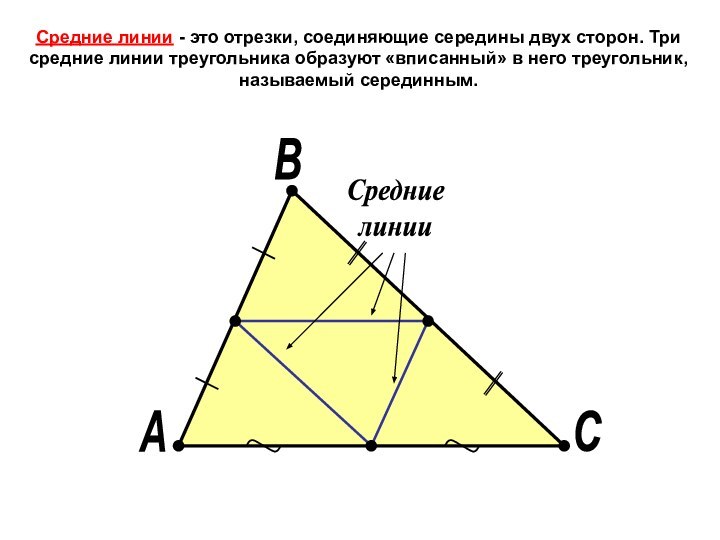
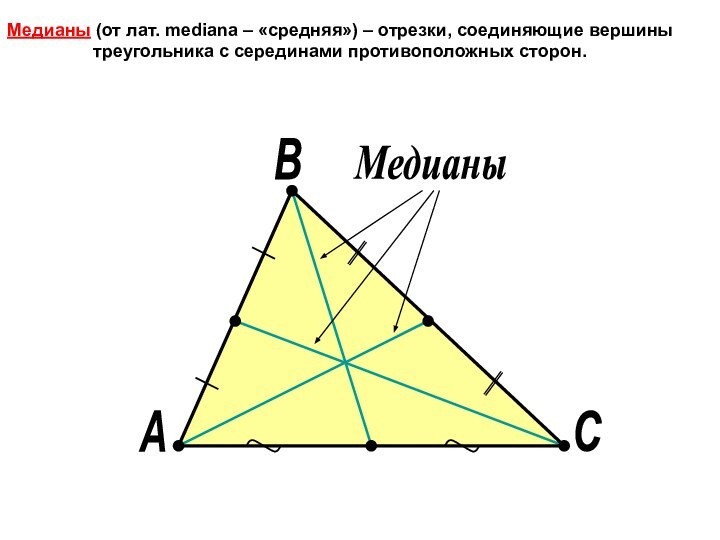
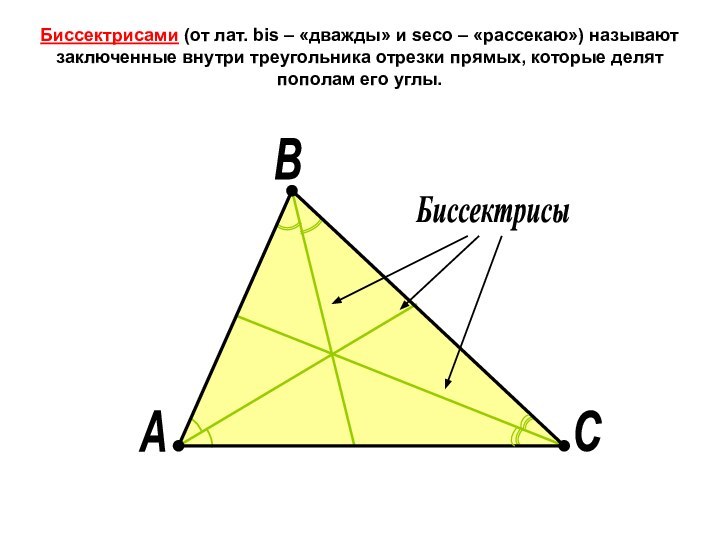
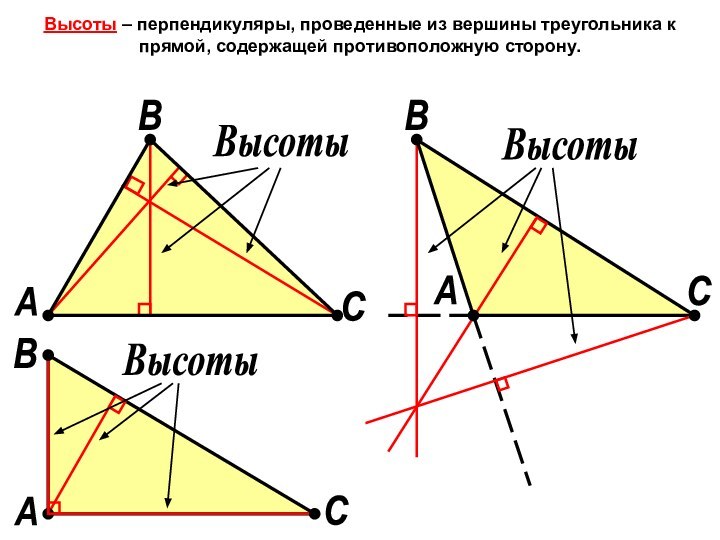
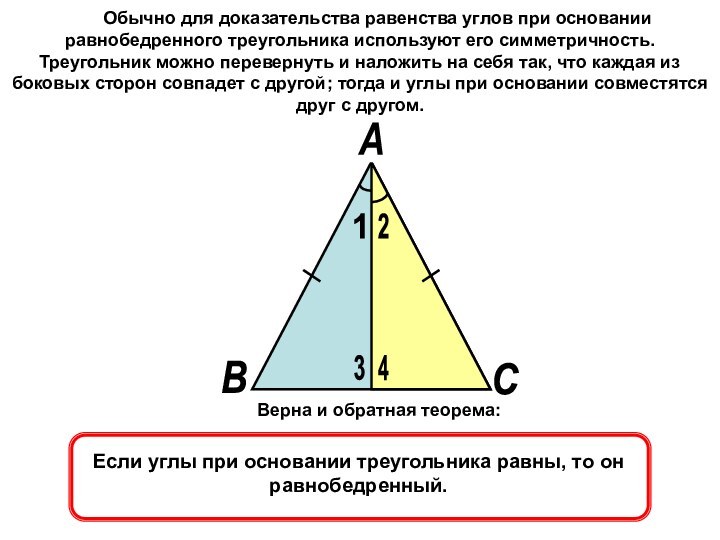
это признак, т. е. достаточное условие того, что он

равнобедренный.
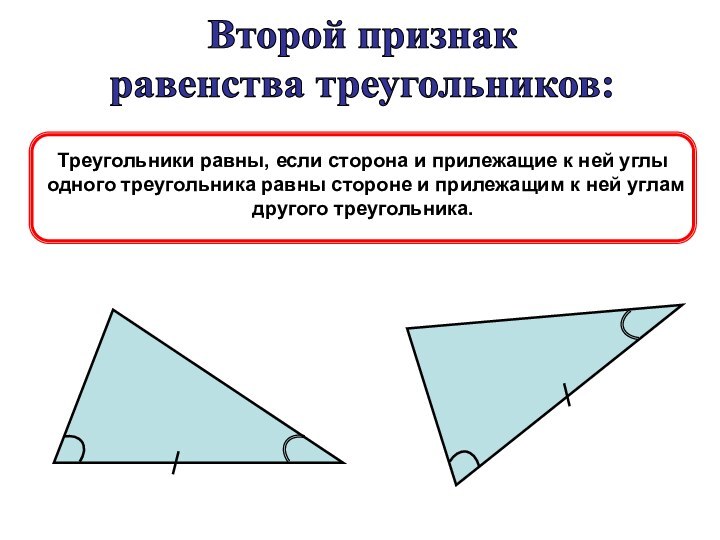
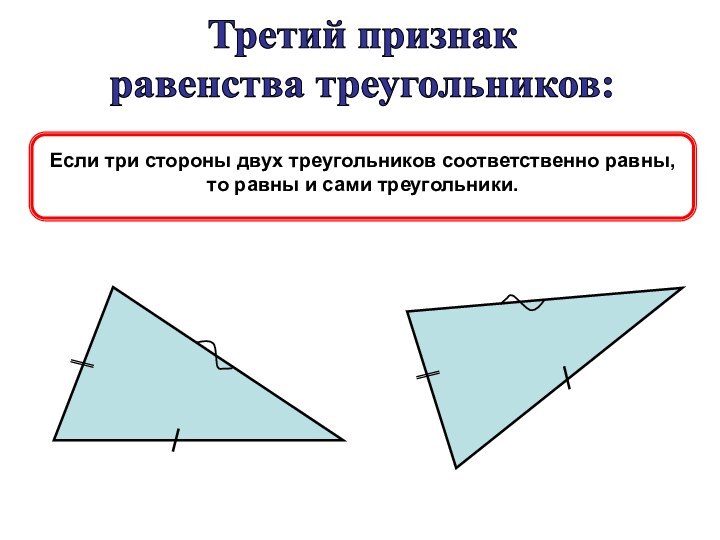
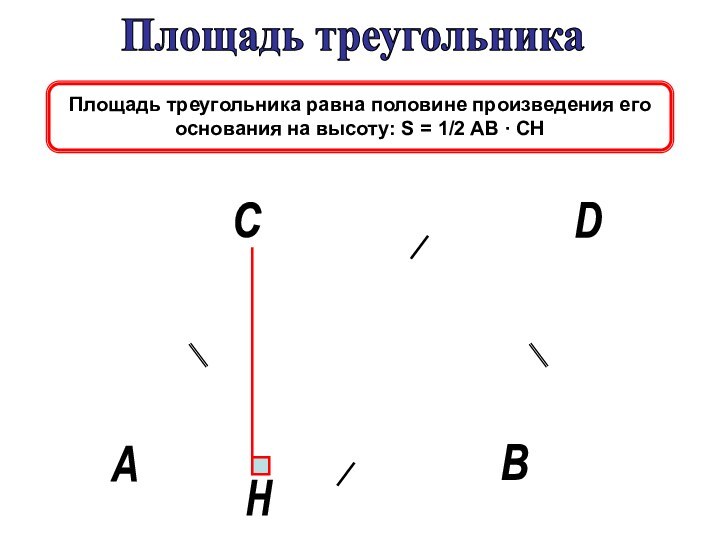
Есть и другие признаки. Например, треугольник будет равнобедренным, если любые два из трех отрезков – медиана, высота или биссектриса, проведенные к основанию, равны. Вот еще три признака:

Если в треугольнике равны две медианы, или две высоты, или две биссектрисы, то такой треугольник равнобедренный.

Первые два признака доказываются просто. Однако последний, или теорему о том, что треугольник, имеющий две равные биссектрисы, является равнобедренным, доказать довольно сложно. Это так называемая теорема Штейнера – Лемуса. Интересно, что С. Л. Лемус остался в истории математики исключительно потому, что в 1840 г. прислал швейцарскому геометру Якобу Штейнеру письмо с просьбой дать геометрическое доказательство данного факта.

равенства треугольников

Третий признак равенства треугольников
МЕНЮ

стороны и угол, заключенный между ними, то эти треугольники

равны.

А

1

1

С

1

МЕНЮ

к ней углы одного треугольника равны стороне и прилежащим

к ней углам другого треугольника.

МЕНЮ

равны, то равны и сами треугольники.
МЕНЮ

развернутому углу, или 180°.

А
В
С
1
2
3
1
+
2
+
3
=
180°
МЕНЮ

удобнее использовать равносильное свойство внешнего угла треугольника, т. е.

угла, образованного стороной и продолжением другой стороны:

Внешний угол треугольника равен сумме двух внутренних углов, не смежных с ним.

Свойство внешнего угла треугольника

А

В

С

1

2

1

2

МЕНЮ

катетов.
Справедливо и утверждение, обратное теореме Пифагора:
Если стороны треугольника удовлетворяют

равенству
a² + b² = c², то этот треугольник прямоугольный.

Теорема Пифагора

b

c

a

МЕНЮ

на высоту: S = 1/2 AB ∙ CH
А
В
С
Н
D
МЕНЮ

египтяне после каждого разлива Нила заново размечали плодородные участки

его берегов, с которых ушла вода. По Геродоту, с этого и началась геометрия – «землемерие» (от греч. «гео» - «земля» и «метрео» - «измеряю»).
Древние землемеры выполняли геометрические построения, измеряли длины и площади; астрологи рассчитывали расположение небесных светил – все это требовало весьма обширных познаний о свойствах плоских и пространственных фигур, и в первую очередь о треугольнике.
Знакомый всем треугольник по праву считается простейшей из фигур: любая плоская, т. е. простирающаяся в двух измерениях, фигура должна содержать хотя бы три точки, не лежащие на одной прямой. Если соединить эти точки попарно прямолинейными отрезками, то построенная фигура и будет треугольником. Так же называют и заключенную внутри образовавшегося контура часть плоскости.

МЕНЮ