Презентация на тему Треугольники

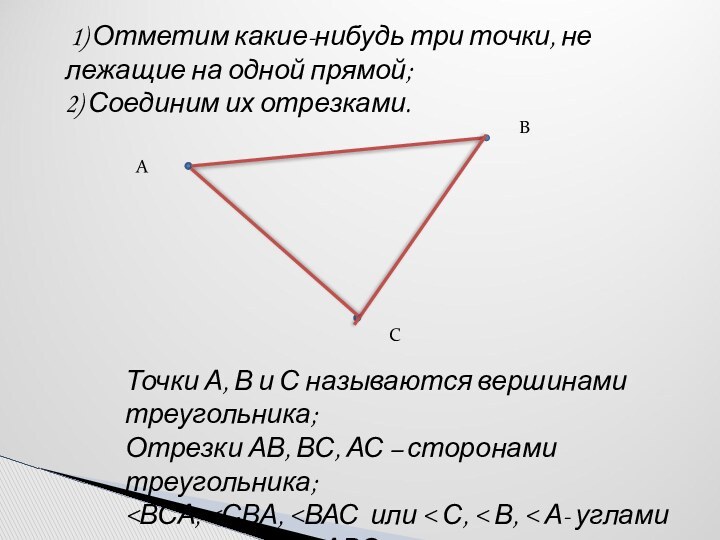
три точки, не лежащие на одной прямой; 2) Соединим их

отрезками.

А

В

С

Точки А, В и С называются вершинами треугольника;
Отрезки АВ, ВС, АС – сторонами треугольника;
<ВСА, <СВА, <ВАС или < С, < В, < А- углами треугольника АВС

наложением

На рисунке треугольники АВС и А1 В1 С1

равны.

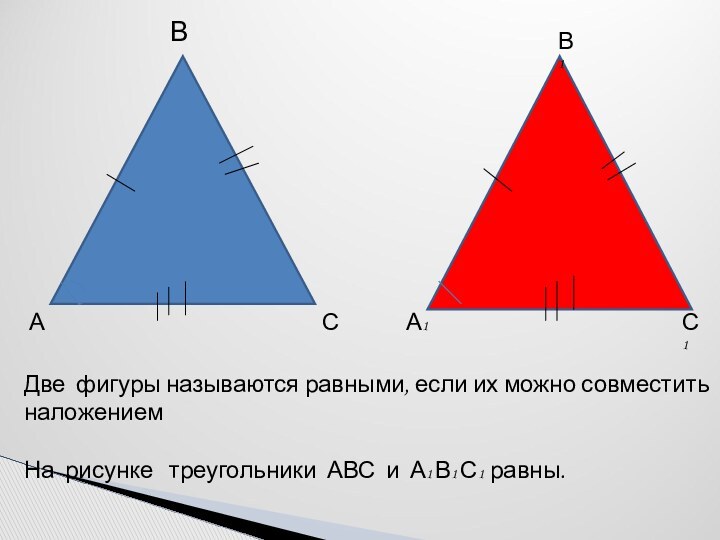
А

В

С

А1

В1

С1

равные углы, и обратно:
Против соответственно равных углов лежат равные

стороны:

А

В

С

А1

В1

С1

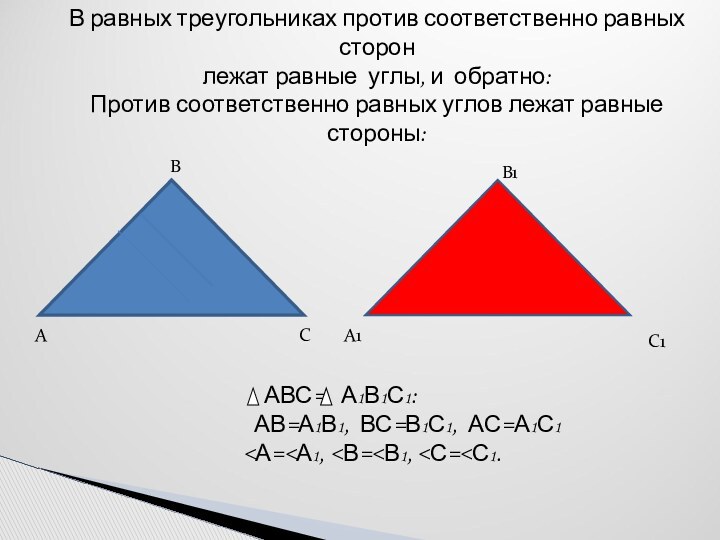
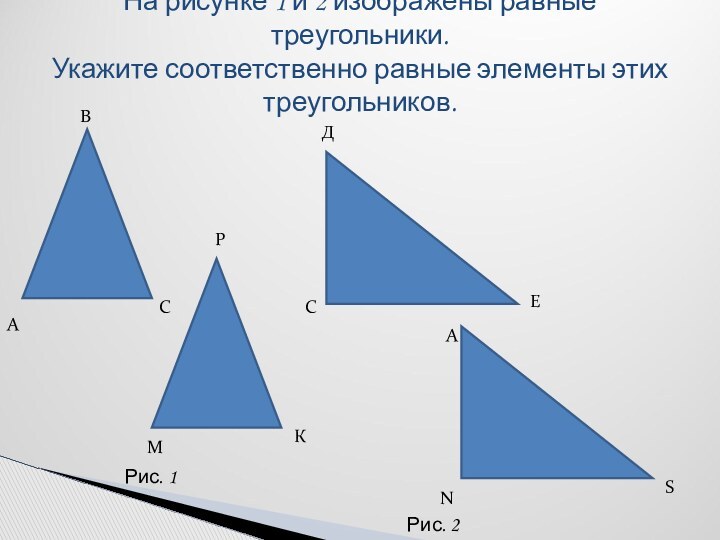
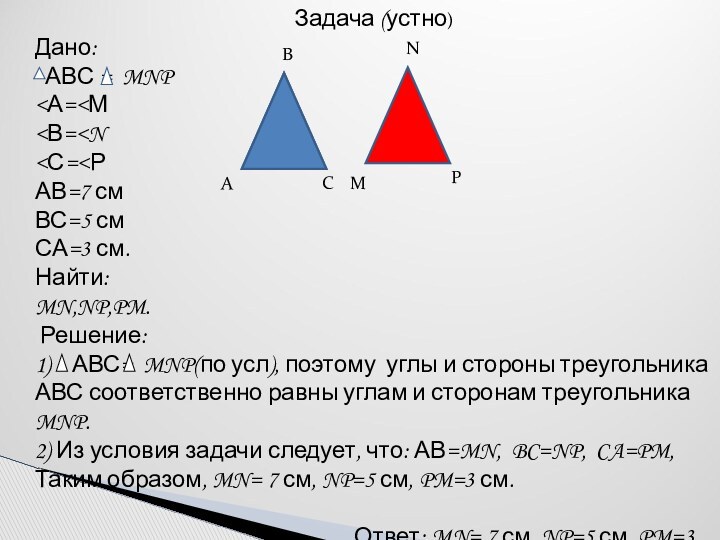
АВС= А1В1С1:
АВ=А1В1, ВС=В1С1, АС=А1С1
<А=<А1, <В=<В1, <С=<С1.

является противолежащей вершине К;
Сторона N К является противолежащей вершине

М.

Угол М заключен между сторонами МК и МN;
Угол N заключен между сторонами NМ и NK;
Угол K заключен между сторонами К Mи KN;

соединяющий вершину А с серединой противоположной стороны. 2) Начертите треугольник

MNP. На стороне МР отметьте произвольную точку К и соедините ее с вершиной, противолежащей стороне МР. 3) Назовите углы: а) треугольника ДЕК , прилежащие к стороне ЕК; б) треугольника MNP, прилежащие к стороне MN. 4) Между какими сторонами : а) треугольника ДЕК заключен угол К; б) треугольника MNP, заключен угол N ?

РАВС=48 см,
АС=18 см,
ВС-АВ=4,6 см.
Найти:
АВ-?
ВС-?
Решение:
Обозначим длину стороны

АВ в см буквой х, тогда ВС=(х+4,6)см;
Р=АВ+ВС+АС
48=х+(х+4,6)+18
2х+22,6=48
Х=(48-22,6):2
Х=12,7 см; Итак, АВ=12,7см, ВС=(12,7+4,6)=17,3 см.
Ответ: АВ=12,7 см , ВС=17,3 см.

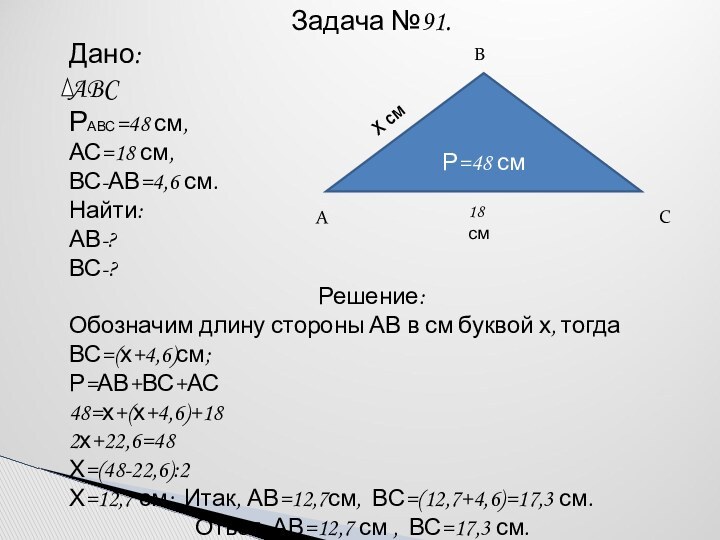
Р=48 см

А

В

С

18 см

Х см

соответственно равные элементы этих треугольников.




А
В
С
М
Р
К
С
Д
Е
А
N
S
Рис. 1
Рис. 2

см.
Найти:
MN,NP,PM.

Решение:
1) АВС= MNP(по усл), поэтому углы и стороны треугольника АВС соответственно равны углам и сторонам треугольника MNP.
2) Из условия задачи следует, что: АВ=MN, BC=NP, CA=PM,
Таким образом, MN= 7 см, NP=5 см, PM=3 см.

Ответ: MN= 7 см, NP=5 см, PM=3 см.

В

А

С

М

Р

N