- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Тригонометрические уравнения
Содержание
- 2. Цели урока:Повторить основные формулы и методы решения тригонометрических уравнений;Закрепить умения и навыки решения тригонометрических уравнений;
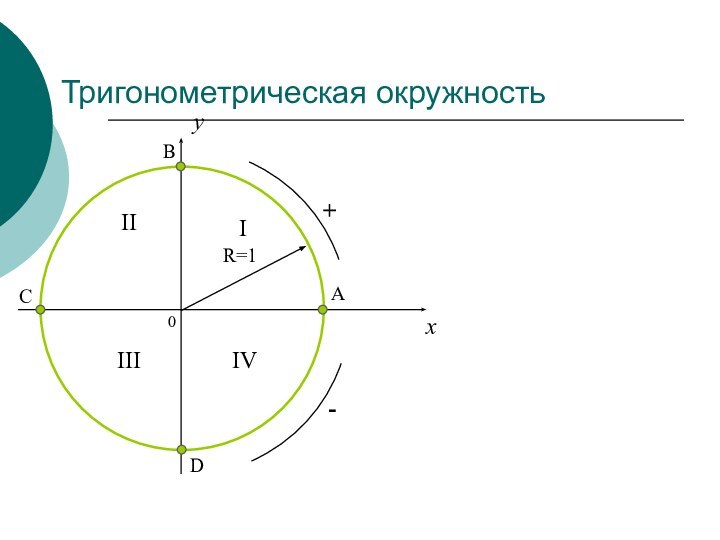
- 3. Тригонометрическая окружность0xyIIIIIIIV
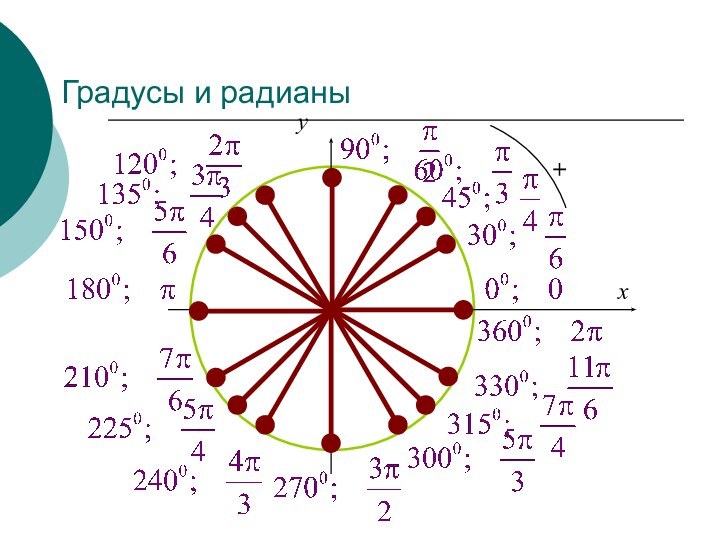
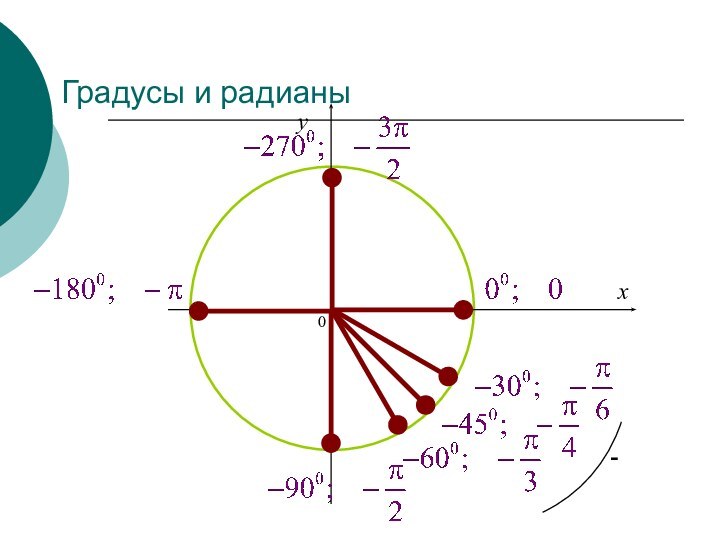
- 4. Градусы и радианы0xy
- 5. Градусы и радианы0xy
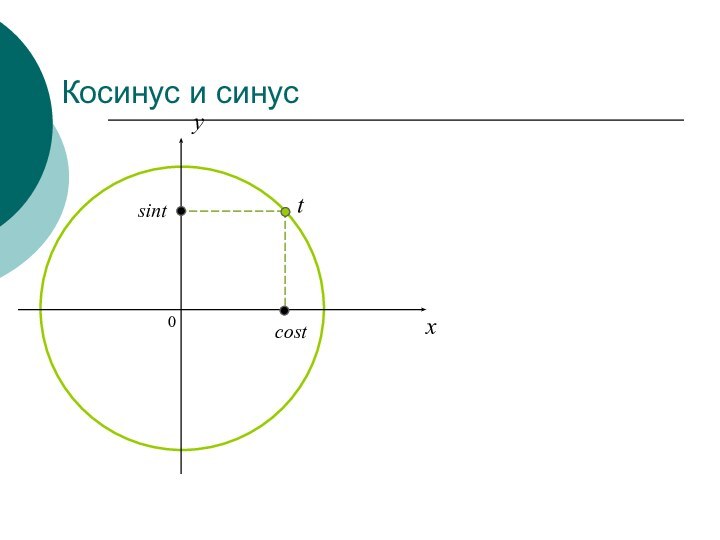
- 6. Косинус и синус0xycostsintt
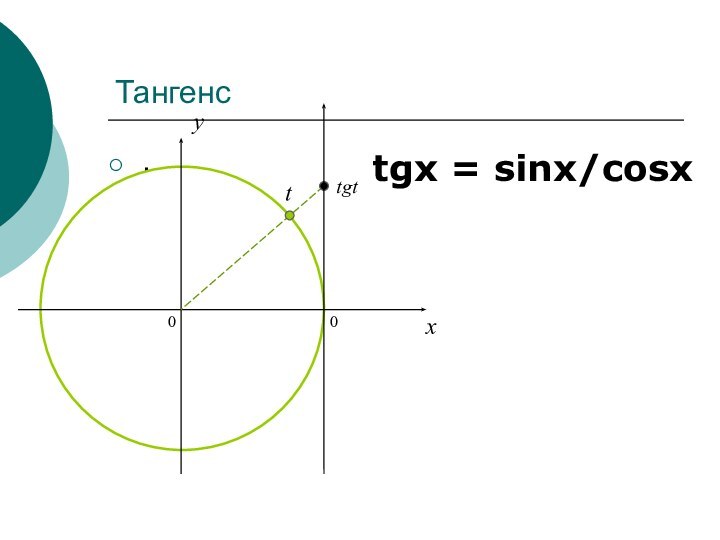
- 7. Тангенс.tgx = sinx/cosx0xytgtt0
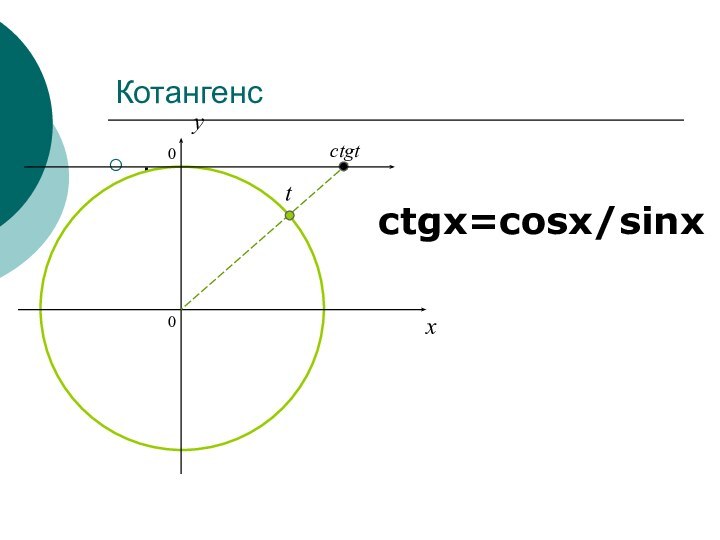
- 8. Котангенс.ctgx=cosx/sinx0xyctgtt0
- 9. Уравнение cost = a1.Проверить условие: a ≤ 12.Записать общее решение уравнения:Где t= arccos a0xyat1-t1-11
- 11. Уравнение sint = a0xy2. Записать общее решение уравнения:1. Проверить условие | a | ≤ 1at1π-t1-11
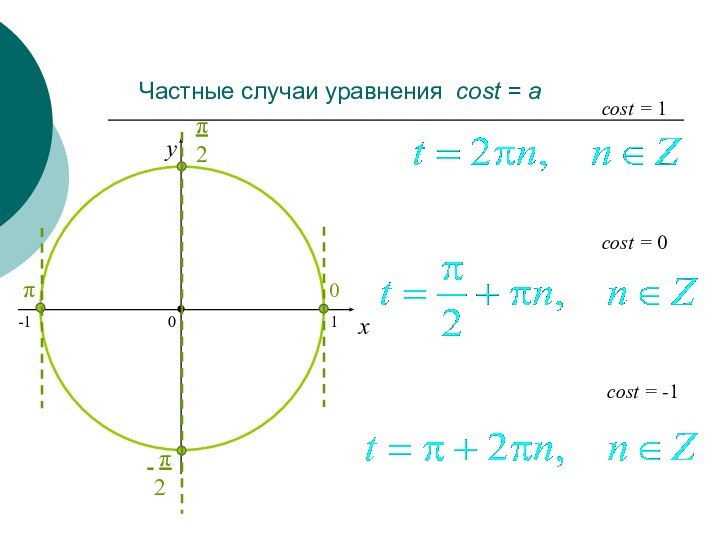
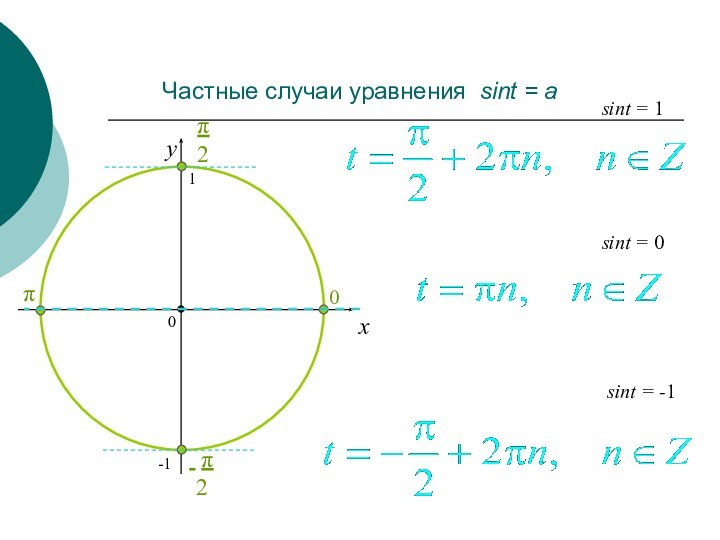
- 12. Частные случаи уравнения sint = axysint = 0sint = -1sint = 1
- 13. Примеры решения тригонометрических уравнений
- 15. sin 2x + sin x= 0
- 16. 4 tg x – 3 ctg
- 18. Первое внимание На Аргументы обрати. Удобно
- 19. Второе внимание на Функции смотри.
- 20. Пример не подчиняется, Решить не получается, Тогда попробуй – «выноси»
- 21. Четвертая ступень «Деление» проверь. (: cosα, : cos²α)
- 22. Скачать презентацию
- 23. Похожие презентации
Цели урока:Повторить основные формулы и методы решения тригонометрических уравнений;Закрепить умения и навыки решения тригонометрических уравнений;



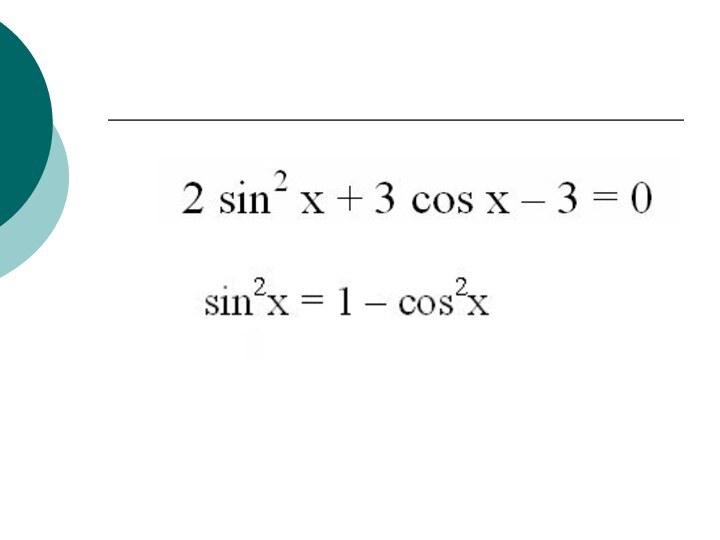
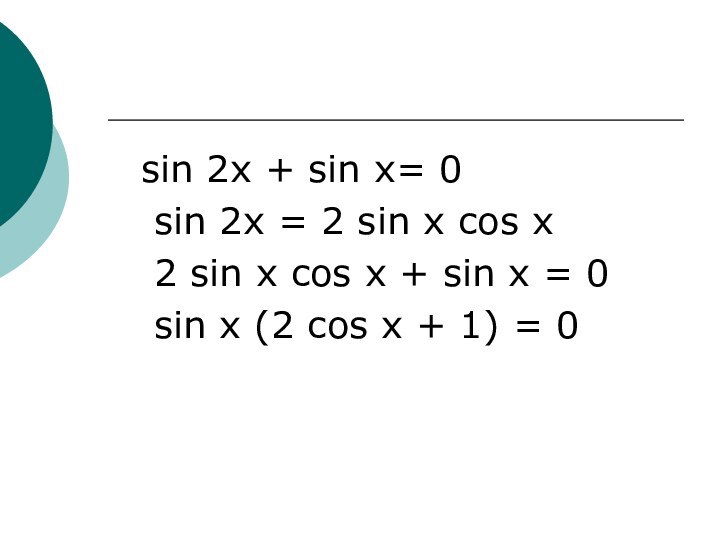
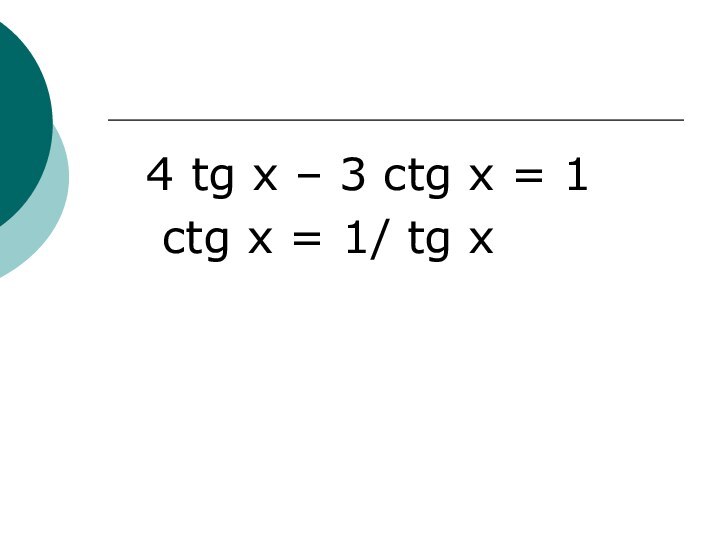






Слайд 9
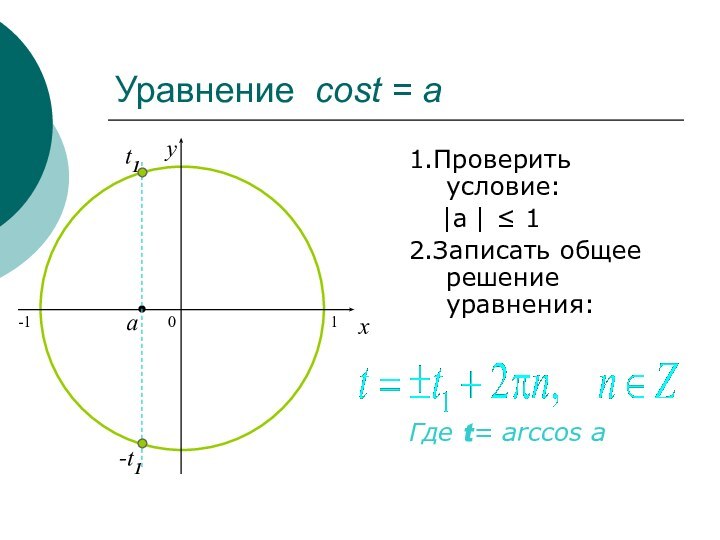
Уравнение cost = a
1.Проверить условие:
a
≤ 1
2.Записать общее решение уравнения:
Где t= arccos a
0
x
y
a
t1
-t1
-1
1
Слайд 11
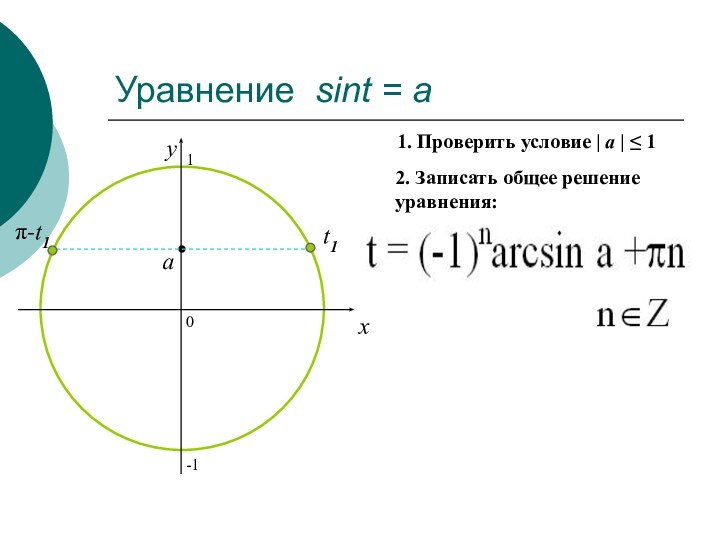
Уравнение sint = a
0
x
y
2. Записать общее решение уравнения:
1.
Проверить условие | a | ≤ 1
a
t1
π-t1
-1
1
Слайд 18
Первое внимание
На Аргументы обрати.
Удобно к
одинаковым
Аргументам перейти.
Для этого - где угол
видишь 2α, 4α = 2 *2 α; α/2; α ± π;α ± π/2; (α ± β)…-
По формулам распиши.
Слайд 19
Второе внимание
на Функции смотри.
К одним и тем же функциям
Старайся перейти.
Для этого по формулам
Сделай переход:
ctq α tq α sin² α
cos² α sin4 α = (sin² α)²