А
В
D
х
у
М(t1)
P(t2)
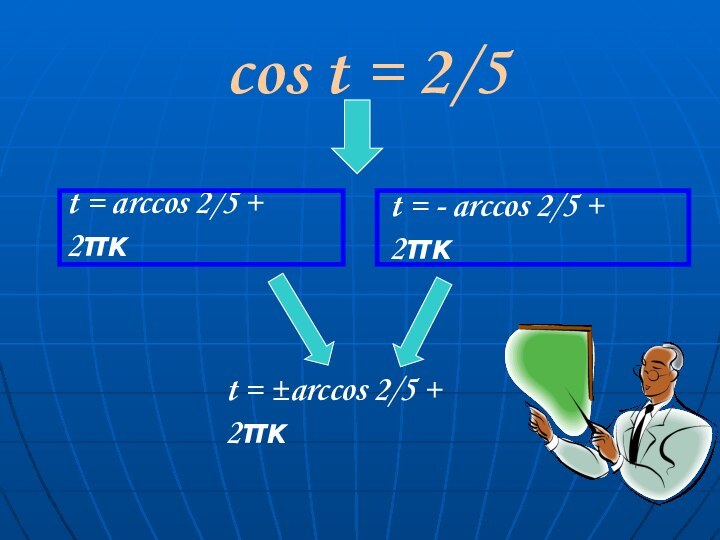
x=2/5
Рис. 1
t =
t1 + 2πκ, t = t2 + 2πκ,
где t1 – длина дуги АМ,
а t2 = - t1
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Тригонометрические уравнения. Арксинус
Содержание
- 2. cos t = acos t = 2/5С
- 3. t1 є [ 0; π/2 ]arccos 2/5
- 4. cos t = 2/5 t = arccos
- 5. Что же такое arccos 2/5? Это число
- 6. cos t = acos t = -
- 7. Что же такое arccos (-2/5)?Это число (длина
- 8. ОпределениеЕсли |а|≤1, то arccos a (арккосинус а)
- 9. Общий вывод о решении уравнения cos t
- 10. ПримерВычислить: arccos ½Решение:Пусть arccos ½ = t.
- 11. ТеоремаДля любого а є [-1;1] выполняется равенство
- 12. Скачать презентацию
- 13. Похожие презентации
cos t = acos t = 2/5С О А ВD х у М(t1) P(t2) x=2/5Рис. 1t = t1 + 2πκ, t = t2 + 2πκ,где t1 – длина дуги АМ, а t2 = - t1
![t1 є [ 0; π/2 ]arccos 2/5 t1 = arccos 2/5 t2](/img/tmb/12/1119566/018c622829e911dee00e8ad5fc12a7f0-720x.jpg "Тригонометрические уравнения. Арксинус")
![ТеоремаДля любого а є [-1;1] выполняется равенство arccos a + arccos (-a)](/img/tmb/12/1119566/16192b9188ee8f1a6be1181770320069-720x.jpg "Тригонометрические уравнения. Арксинус")
Слайд 5
Что же такое arccos 2/5?
Это число (длина
дуги АМ), косинус которого равен 2/5 и которое принадлежит
отрезку [ 0; π/2 ].
Слайд 6
cos t = a
cos t = - 2/5
t
= t1+ 2πκ,
t = t2 + 2πκ,
где
t1 – длина дуги АМ, а t2 = - t1
О
В
D
А
С
у
х
М(t1)
P(t2)
x= - 2/5
t = arccos (-2/5) + 2πκ
t = - arccos (-2/5) + 2πκ
t = ±arccos 2/5 + 2πκ
Слайд 7
Что же такое arccos (-2/5)?
Это число (длина дуги
АМ), косинус которого равен -2/5 и которое принадлежит отрезку
[ π/2; π].
Слайд 8
Определение
Если |а|≤1, то arccos a (арккосинус а) –
это такое число из отрезка [ 0; π], косинус
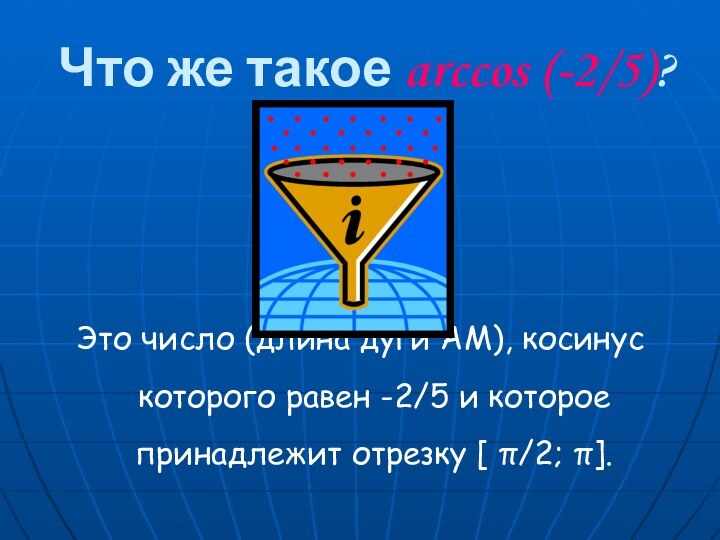
которого равен а.Если |а|≤1, то
arccos a = t
cos t =a,
0 ≤ t ≤ π.
Слайд 9
Общий вывод о решении уравнения cos t =a
Если
|а|≤1, то уравнение cos t = a имеет решения
t
= ±arccos a + 2πκ, k є Z
Слайд 10
Пример
Вычислить: arccos ½
Решение:
Пусть arccos ½ = t. Тогда
cos t = ½ и
t є [ 0;
π]. Значит, t = π/3, поскольку cos π/3 = ½ и π/3 є [ 0;
π]. Итак, arccos ½ = π/3.
Слайд 11
Теорема
Для любого а є [-1;1] выполняется равенство
arccos
a + arccos (-a) = π.
D
О
В
А
С
у
х
- а
а
М
Р
arccos a + arccos (-a) = AM + AP = PC +AP = AC = π
