- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Уравнения с частными производными (II)
Содержание
- 2. Одним из наиболее распространенных уравнений с частными
- 3. Одномерное волновое уравнение описывает продольные колебания стержня, сечения которого совершают плоскопараллельные колебательные движения.
- 4. Двумерное волновое уравнение используется для исследования колебаний тонкой пластины (мембраны).
- 5. Трехмерное волновое уравнение описывает распространение волн в пространстве (например, звуковых волн в жидко- жидкости).
- 6. Рассмотрим одномерное волновое уравнениеc начальными условиями
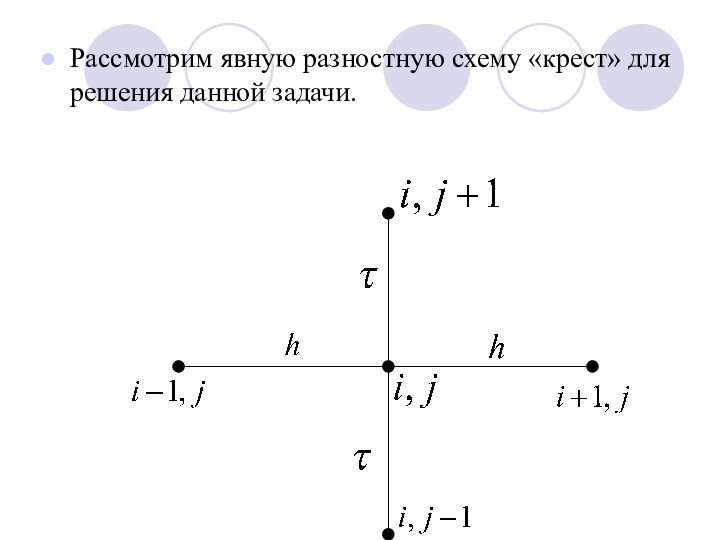
- 7. Рассмотрим явную разностную схему «крест» для решения данной задачи.
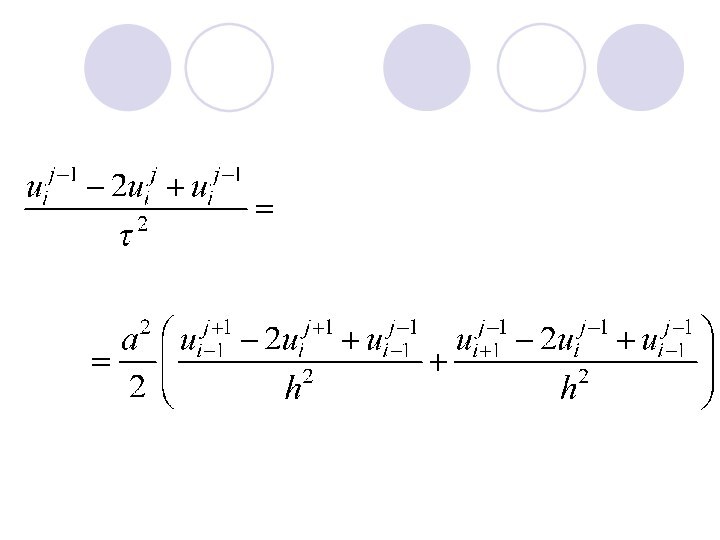
- 8. Заменим в уравнении вторые производные искомой функции U по t и х их конечно-разностными соотношениями.
- 9. Отсюда можно найти явное выражение для значения сеточной функции на (j + 1)-м слое:
- 10. Здесь, для определения неизвестных значений на (j
- 11. решения на нулевом и первом слоях находятся с помощью начальных условий.На нулевом слое имеем
- 12. Для получения решения на первом слое воспользуемся
- 13. Построим неявную схему. Вторую производную по t
- 15. Из этого соотношения можно получить систему уравнений
- 16. ИНТЕГРАЛЬНЫЕ УРАВНЕНИЯ Интегральным уравнением называется уравнение, неизвестная
- 17. Виды интегральных уравнений. Уравнения, в которые искомая функция входит линейно, называются линейными интегральными уравнениями.
- 18. Одним из них является уравнение Фредгольма первого рода Уравнение Фредгольма второго рода имеет вид
- 19. уравнение Вольтерра первого рода: уравнение Вольтерра второго рода
- 20. Скачать презентацию
- 21. Похожие презентации
Одним из наиболее распространенных уравнений с частными производными второго порядка является волновое уравнение, описывающее различные виды колебаний.
















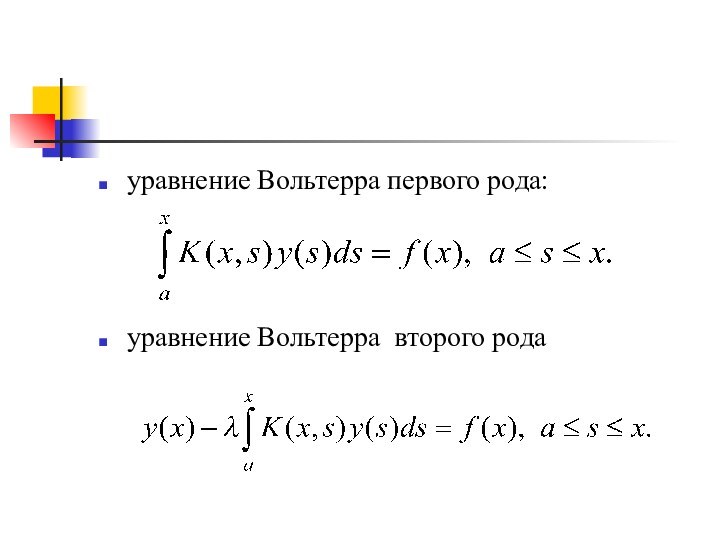

Слайд 3 Одномерное волновое уравнение описывает продольные колебания стержня, сечения
которого совершают плоскопараллельные колебательные движения.
Слайд 4 Двумерное волновое уравнение используется для исследования колебаний тонкой
пластины (мембраны).
Слайд 5 Трехмерное волновое уравнение описывает распространение волн в пространстве
(например, звуковых волн в жидко- жидкости).
Слайд 8 Заменим в уравнении вторые производные искомой функции U
по t и х их конечно-разностными соотношениями.
Слайд 10 Здесь, для определения неизвестных значений на (j +
1)-м слое нужно знать решения на j-м и (j
— 1)-м слоях.Поэтому начать счет можно лишь для второго слоя.
Слайд 11 решения на нулевом и первом слоях находятся с
помощью начальных условий.
На нулевом слое имеем
Слайд 12 Для получения решения на первом слое воспользуемся вторым
начальным условием.
Производную
заменим конечно-разностной аппроксимацией.Из этого соотношения можно найти значения сеточной функции на первом слое:





























