- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Вектор
Содержание
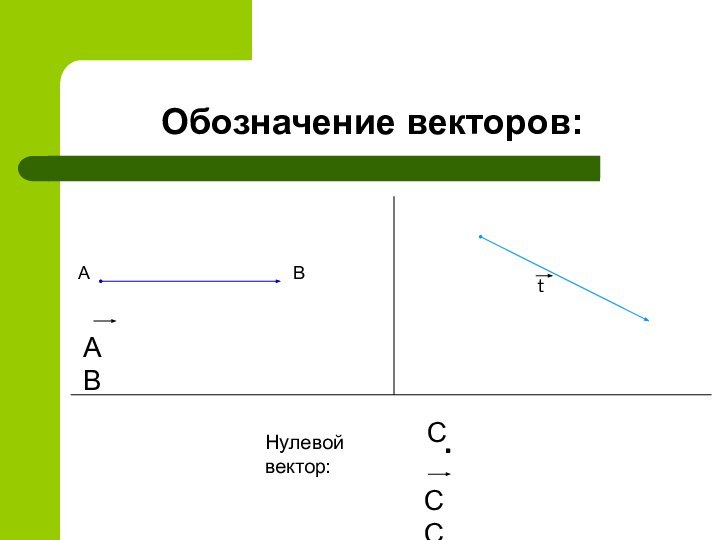
- 2. Обозначение векторов:АВАВt.СССНулевой вектор:
- 3. Типы векторов:
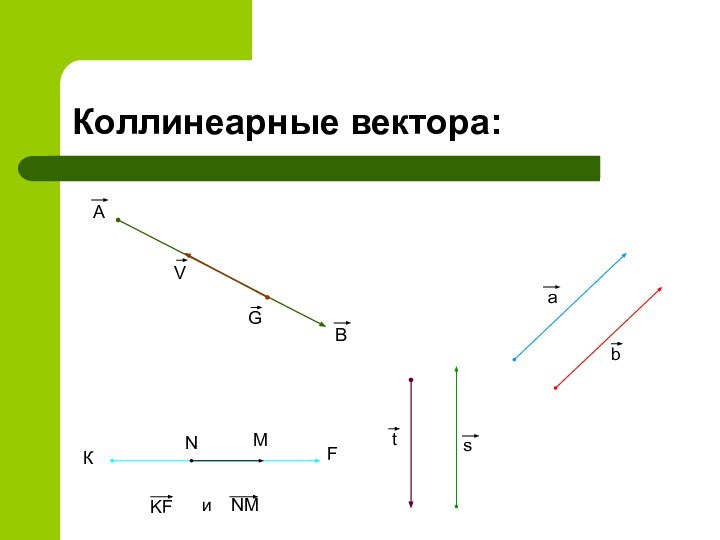
- 4. Коллинеарные вектора:аbКFNMKFиNMABVGst
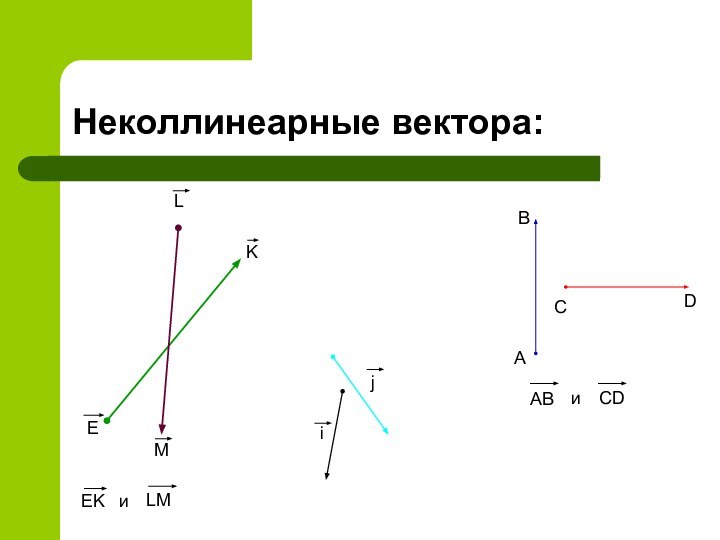
- 5. Неколлинеарные вектора:АВСDABиCDEKLMEKиLMji
- 6. Сонаправленные вектора:Сонаправленные вектора – коллинеарные вектора, направленные в одну сторону.ababABCACCBABAC
- 7. Противоположнонаправленные вектора:Противоположнонаправленные вектора – коллинеарные вектора, направленные в противоположные стороны.efAOBOAOB
- 8. Сложение векторов
- 9. Правило сложения треугольника:AB + BC = AC
- 10. Правило параллелограмма:a + b = b +
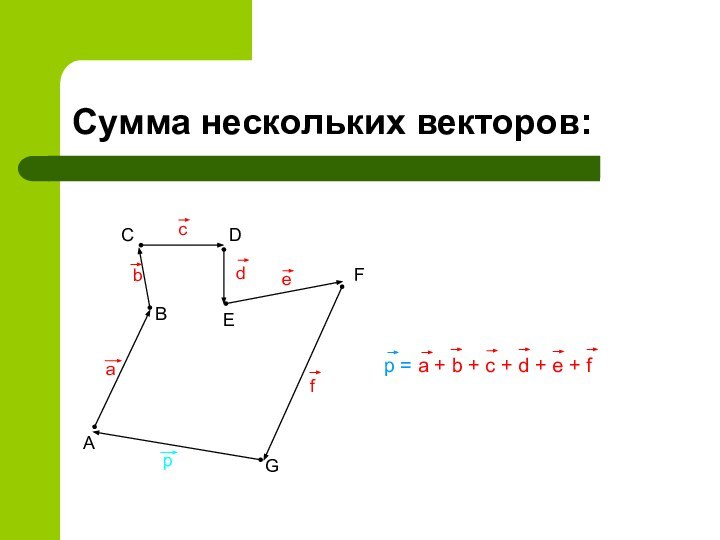
- 11. Сумма нескольких векторов:ABCDEFGabcdefp = a + b + c + d + e + f p
- 12. Разность векторов:Для любых векторов a и b
- 13. Умножение вектора на число:(kl) • a =
- 14. Скачать презентацию
- 15. Похожие презентации
Обозначение векторов:АВАВt.СССНулевой вектор:





Слайд 6
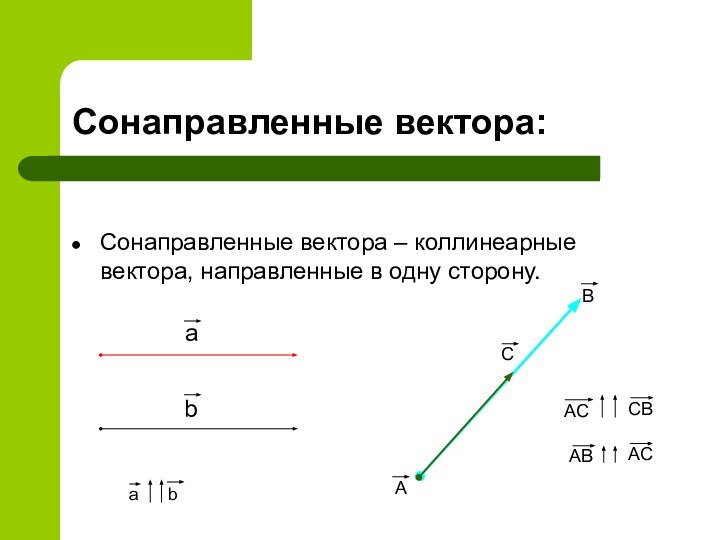
Сонаправленные вектора:
Сонаправленные вектора – коллинеарные вектора, направленные в
одну сторону.
Слайд 7
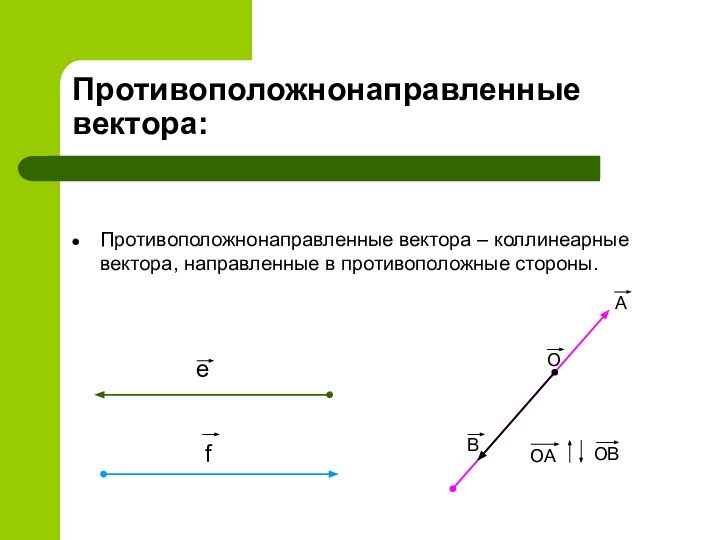
Противоположнонаправленные вектора:
Противоположнонаправленные вектора – коллинеарные вектора, направленные в
противоположные стороны.
e
f
A
O
B
OA
OB
Слайд 9
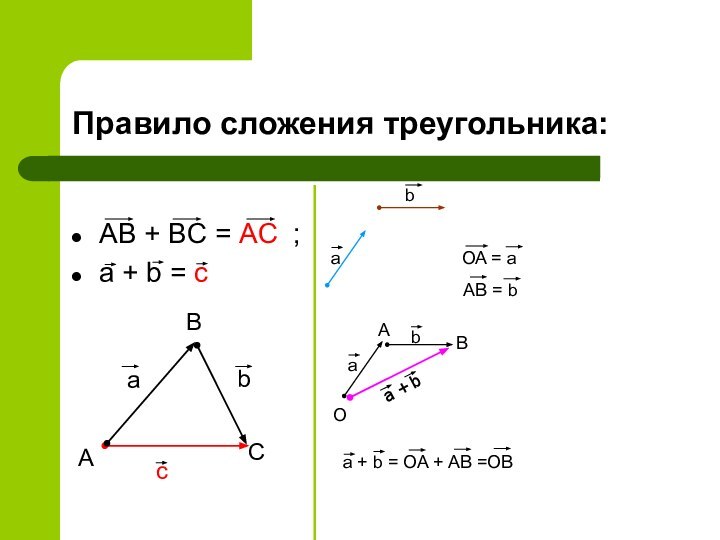
Правило сложения треугольника:
AB + BC = AC ;
a
+ b = c
a
b
c
A
B
C
a
b
OA = a
AB = b
O
A
B
a
b
a +
ba + b = OA + AB =OB
Слайд 10
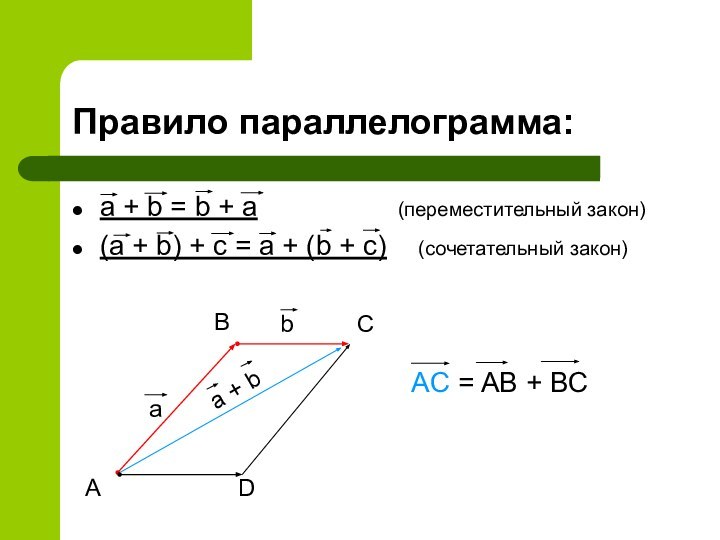
Правило параллелограмма:
a + b = b + a
(переместительный
закон)(a + b) + c = a + (b + c) (сочетательный закон)
A
B
C
D
a
b
a + b
AC = AB + BC
Слайд 12
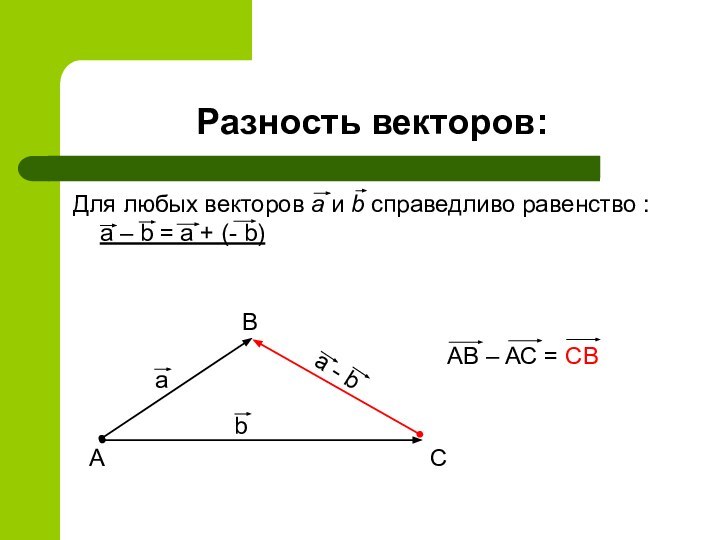
Разность векторов:
Для любых векторов a и b справедливо
равенство : a – b = a + (-
b)A
B
C
a
b
a - b
AB – AC = CB
Слайд 13
Умножение вектора на число:
(kl) • a = k
• (la) (сочетательный закон)
(k + l) • a =
ka + la (первый распределительный закон)k (a + b) = ka + kb (второй распределительный закон)
k, l – числа ; a, b - вектора
a
b
c
b = 3a
c = -4a
b = ka, где k – число, a = 0
|b| = |k| • |a|
b a , если k > 0
b a , если k < 0