- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Великие задачи математики. Квадратура круга
Содержание
- 2. Автор: Монахов Станислав МОУ "Средняя общеобразовательная школа № 59"Курск - 2006
- 3. Меня зовут Монахов Станислав. Я ученик
- 4. Впервые я услышал о трех знаменитых задачах
- 5. Показать, что в математике, как и во
- 6. Возьму линейку, проведу прямую,
- 7. С глубокой древности известны три
- 8. Вероятно, задача была известна уже
- 9. В папирусе Ринда, написанным Ахмесом,
- 10. Древнегреческие математики также достигли чрезвычайно
- 12. Но первая прямая ссылка на неё относится
- 13. Полного решения, предложенного Антифонтом, не сохранилось,
- 15. Но, так как для любого
- 17. Известный математик древности Гиппократ Хиосский (ок. 400
- 18. Попытки Гиппократа решить задачу о
- 19. Найденное Гиппократом Хиосским соотношение позволило
- 20. Они впоследствии получили название гиппократовых луночек. Казалось
- 21. Были найдены и другие пути
- 22. Все предложенные решения в лучшем случае давали
- 23. Один из самых громких споров на
- 24. Однако ученых Древней Греции и
- 25. Отношение длины окружности к ее диаметру есть
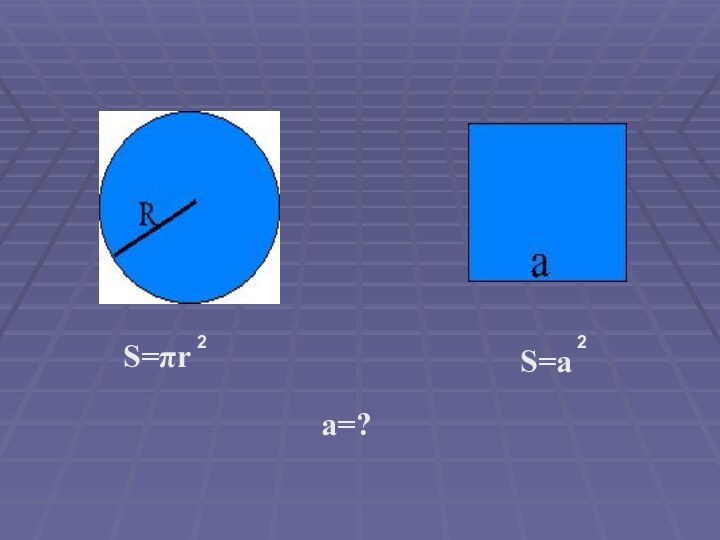
- 26. S=r 2 S=a a=?
- 27. Этот результат вместе с формулой
- 28. Работа, сделанная Шенксом, в сущности бесполезна –
- 29. Можно вычислить приближенное значение П.
- 30. Поэтому квадратура круга была в
- 31. Лишь в 80-х годах 19в. было строго
- 32. Термин «квадратура круга» стал синонимом неразрешимых задач.
- 33. Скачать презентацию
- 34. Похожие презентации
Автор: Монахов Станислав МОУ "Средняя общеобразовательная школа № 59"Курск - 2006































Слайд 3 Меня зовут Монахов Станислав. Я ученик 6-го класса,
очень люблю заниматься математикой, историей, информатикой, а также много
читать и считаю, что как бы ни относились люди к математике, без нее - как без рук. Она - повсюду. Нужно только уметь ее увидеть. Огромную помощь в этом оказывают научно-популярная и справочная литература, Интернет, позволяющие взглянуть на поставленную задачу с новой, нестандартной точки зрения.Слайд 4 Впервые я услышал о трех знаменитых задачах на
факультативном занятии по математике «Наглядная геометрия» от учителя. Из
них меня особенно заинтересовала квадратура круга.Во-первых, очень удивило сочетание слов «квадратура», «круг».
Во-вторых, чем знаменита эта задача.
В- третьих, почему её решением так долго занимались великие ученые.
В-четвертых, целесообразность решения данной задачи и её практическая значимость.
Эти вопросы меня очень заинтриговали и я решил проследить историю возникновения и решения данной задачи.
Введение
Слайд 5
Показать, что в математике, как и во всякой
другой науке, достаточно своих неразгаданных тайн.
Подчеркнуть, что математиков
отличает нестандартное мышление. А иногда смекалка и интуиция хорошего математика просто приводят в восхищение! Показать, что сама попытка решения задачи о квадратуре круга содействовала развитию новых понятий и идей в математике.
Учиться работать с различными источниками информации, анализировать и сопоставлять точки зрения ученых разных времен по данной теме.
Продолжить исследовательскую работу по теме « Знаменитые задачи математики»
Цели и задачи проекта
Слайд 6
Возьму линейку, проведу прямую,
И мигом круг квадратом обернётся, Посередине рынок мы устроим, А от него уж улицы пойдут – Ну, как на Солнце! Хоть оно само И круглое, а ведь лучи прямые!..
/Аристофан/
Слайд 7
С глубокой древности известны три задачи
на построение: об удвоении куба, трисекции угла и квадратуре
круга. Они сыграли особую роль в истории математики. В конце концов было доказано, что решить их невозможно, пользуясь только циркулем и линейкой. Но уже сама постановка проблемы «доказать неразрешимость» была смелым шагом вперёд.
Слайд 8
Вероятно, задача была известна уже за
две тысячи лет до н. э. в Древнем Египте
и Вавилоне. В то время у египетских математиков находятся первые решения задачи, как построить квадрат, равновеликий данному кругу, или определить соотношение между окружностью и её диаметром.Слайд 9 В папирусе Ринда, написанным Ахмесом, говорится, что
сторона квадрата, равновеликого площади круга, равна восьми девятым диаметра
(так что П = 3,16). У древних вавилонян и евреев принималось, что длина окружности ровно втрое больше диаметра и, следовательно, П =3.
Слайд 10
Древнегреческие математики также достигли чрезвычайно большого
искусства в геометрических построениях. Они еще издавна преобразовывали любую
прямолинейную фигуру с помощью циркуля и линейки в произвольную прямолинейную, равновеликую ей.Слайд 11
Так
появилась мысль обобщить эту задачу: построить с помощью циркуля и линейки такой квадрат, площадь которого была бы равна площади данного круга. Задача получила название квадратуры круга, и многие ученые пытались выполнить такое построение. Однако решение не поддавалось их усилиям.Слайд 12 Но первая прямая ссылка на неё относится к
V в. до н. э. По свидетельству древнегреческого историка
Плутарха, философ Антифонт, коротая время в тюрьме, пытался квадрировать круг, т. е. превратить его в равновеликий квадрат.Слайд 13 Полного решения, предложенного Антифонтом, не сохранилось, но считается
что оно состояло в следующем: производя последовательно удвоение сторон
вписанного многоугольника, он получал в конце-концов многоугольник с очень большим числом сторон, которые, по мысли Антифонта, должны совпадать с соответствующими им дугами окружности.
Слайд 15
Но, так как для любого многоугольника
можно с помощью циркуля и линейки построить равновеликий квадрат,
то такой квадрат можно построить и для данного круга. От Плутарха известно, что лучшие математики того времени (в том числе Платон, Евдокс) посещали в темнице Антифонта и были удовлетворены его решением, а ведь требования к строгости доказательств в то время были не ниже сегодняшних.Слайд 16
Архимед (287-212 до н.э.), вычисляя периметры вписанных и
описанных96-ти угольников, в сочинении
«Измерение круга» показал,
что периметр вписанного
многоугольника с любым числом
сторон всегда меньше, а
описанного - всегда больше
длины данной окружности, и что
величина П заключается между
пределами 3,1408 < П < 3,1429.
Слайд 17 Известный математик древности Гиппократ Хиосский (ок. 400 г.
до н.э.) первый указал на то, что площадь круга
пропорциональна квадрату его диаметра. Но провести строгое доказательство учёный в то время еще не мог: не было подходящего метода.
Слайд 18
Попытки Гиппократа решить задачу о
квадратуре круга привели его к открытию квадрируемых фигур (то
есть таких, площади которых выражаются в рациональных числах), ограниченных пересекающимися окружностями.
Слайд 19
Найденное Гиппократом Хиосским соотношение позволило свести
задачу о квадратуре круга к построению с помощью циркуля
и линейки, если это возможно, полученного коэффициента пропорциональности, одного и того же для всех кругов.
Слайд 20
Они впоследствии получили название гиппократовых луночек. Казалось бы,
что с появлением таких луночек найден ключ к решению
задачи о квадратуре круга. Она была бы решена, если бы удалось разбить круг на квадрируемые части.
Слайд 21
Были найдены и другие пути определения
квадратуры круга: кроме циркуля и линейки использовали различные инструменты
или специально построенные кривые. Так, в V в. до н.э. греческий математик Гиппий из Элиды изобрел кривую, впоследствии получившую название квадратрисы Динострата (ее назвали по имени другого древнегреческого математика, жившего несколько позже и указавшего способ построения квадратуры круга при помощи этой кривой).
Слайд 22
Все предложенные решения в лучшем случае давали приближённое
значение с достаточно хорошей точностью. Однако все-таки оставались принципиально
приближёнными. Впрочем, авторы таких построений часто не сомневались в их абсолютной точности и горячо отстаивали свои заблуждения.Слайд 23 Один из самых громких споров на эту тему
произошёл в Англии между двумя выдающимися учёными XVII в.,
философом Томасом Гоббсом и математиком Джоном Валлисом. В весьма почтенном возрасте Гоббс опубликовал около десяти «решений» задачи о квадратуре круга.
Слайд 24
Однако ученых Древней Греции и их
последователей такие решения, находящиеся за пределами применения циркуля и
линейки, не удовлетворяли. Будучи вначале чисто геометрической задачей, квадратура круга превратилась в течение веков в исключительно важную задачу арифметико-алгебраического характера, связанную с числом П , и содействовала развитию новых понятий и идей в математике.
Слайд 25
Отношение длины окружности к ее диаметру есть величина
постоянная, не зависящая от радиуса круга, она обозначается буквой
П. Теперь известно, П - число иррациональное, оно выражается бесконечной непериодической десятичной дробью 3,1415926…, которое было вычислено с 707 десятичными знаками математиком В. Шенксом.
Слайд 27
Этот результат вместе с формулой вычислений
он обнародовал в 1837 году. Ни одна ещё задача
подобного рода не решалась с таким огромным приближением и с точностью, далеко превышающее отношение микроскопических расстояний к телескопическим.
Слайд 28
Работа, сделанная Шенксом, в сущности бесполезна – или
почти бесполезна. Но, с другой стороны, она может служить
довольно убедительным доказательством противного тому, кто до сих пор ещё надеется, что можно найти точное отношение длины окружности к диаметру.
Слайд 29
Можно вычислить приближенное значение П. Однако
не в практическом отношении интересовала людей задача о квадратуре
круга, а интересовала её принципиальная сторона: возможно ли точно решить эту задачу, выполняя построения с помощью только циркуля и линейки.
Слайд 30
Поэтому квадратура круга была в прежние
времена самой заманчивой и соблазнительной задачей. Армия «квадратурщиков» неустанно
пополнялась каждым новым поколением математиков. Все усилия были тщетны, но число их не уменьшалось. В некоторых умах доказательство, что решение не может быть найдено, зажигало ещё большее рвение к изысканиям.
Слайд 31
Лишь в 80-х годах 19в. было строго доказано,
что решить задачу о квадратуре круга с помощью циркуля
и линейки невозможно. Эта задача становится разрешимой, если применять, кроме циркуля и линейки, еще другие средства построения.
Слайд 32
Термин «квадратура круга» стал синонимом неразрешимых задач. Вместе
с тем предлагалось множество решений при помощи нетрадиционных инструментов.
Всё это привело к возникновению и развитию совершенно новых идей в геометрии и алгебре. Анализируя материал по данной теме, я пришел к выводу, что неразрешимость некоторых задач служит отправной точкой новых математических исследований, интригует, стимулирует и способствует развитию творчества.В дальнейшем я собираюсь изучить историю решения других знаменитых задач древности о трисекции угла, удвоении куба. В процессе работы я:
систематизировал полученную информацию об истории решения неразрешимых задач,
раньше своих одноклассников познакомился с числом П, и с задачами на построения с помощью циркуля и линейки,
приобрёл навыки :
исследовательской работы,
самостоятельного поиска и нахождения ключевых понятий,
научился производить группировку материала и его анализ.
Заключение





























