- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Вписанная окружность
Содержание
- 2. Цели урока:1.Познакомится с определением вписанной окружности. 2.Изучить доказательство теоремы о вписанной окружности.3.Решение задач по данной теме.
- 3. Устная работаOMKNД а н о: MO =
- 4. Так четырехугольник EFNM описан около окружности,а четырехугольник
- 5. В любой треугольник можно вписать окружность.Т е о р е м а
- 6. Д а н о:∆ ABCД о к
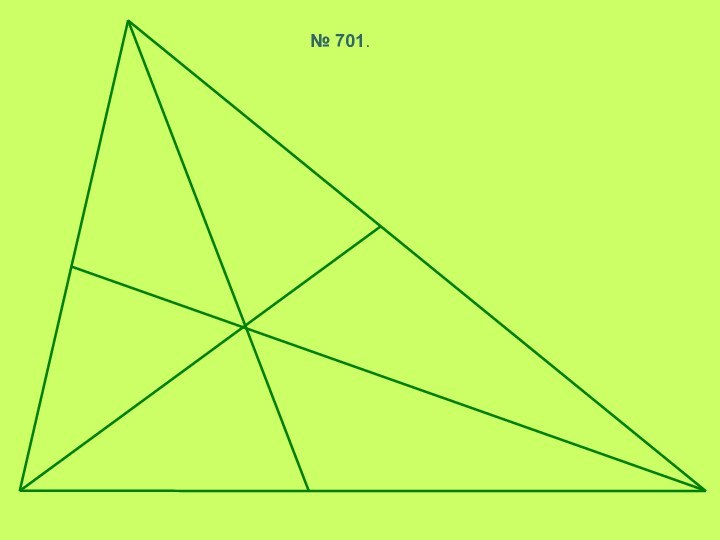
- 7. № 701.
- 8. Скачать презентацию
- 9. Похожие презентации
Цели урока:1.Познакомится с определением вписанной окружности. 2.Изучить доказательство теоремы о вписанной окружности.3.Решение задач по данной теме.




Слайд 2
Цели урока:
1.Познакомится с определением вписанной окружности.
2.Изучить доказательство
теоремы о вписанной окружности.
Слайд 3
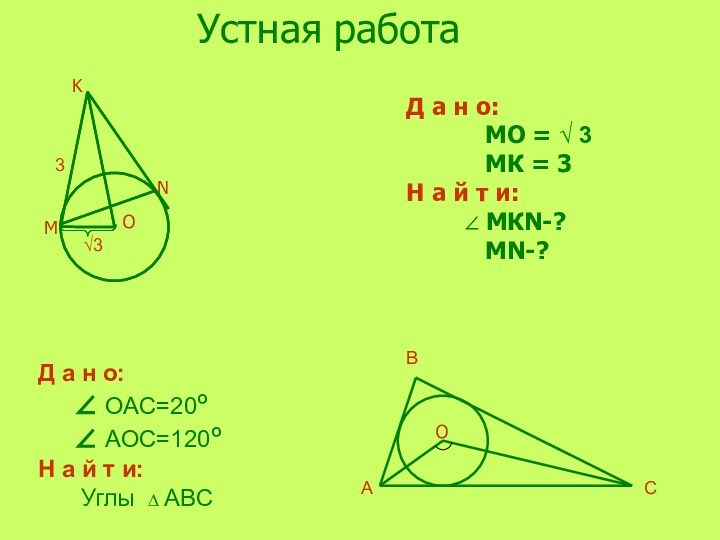
Устная работа
O
M
K
N
Д а н о:
MO = √
3
МК = 3
Н а й т и:
МКN-?MN-?
√3
O
B
C
A
Д а н о:
OAC=20º
АOC=120º
Н а й т и:
Углы ∆ АBC
3
Слайд 4
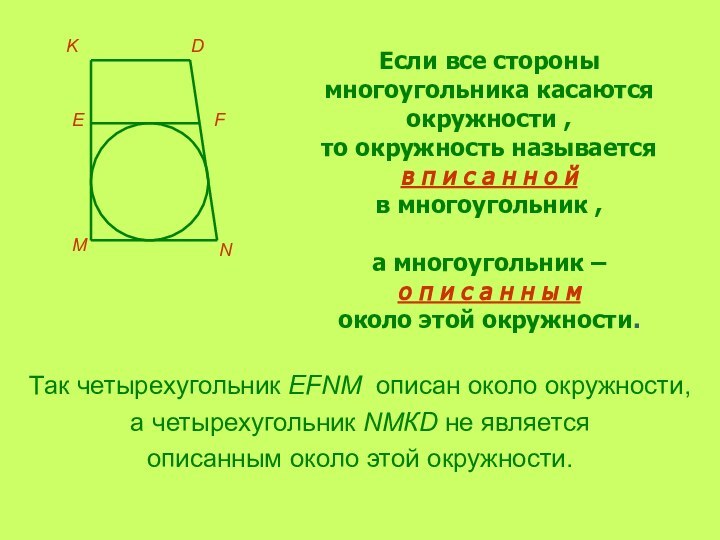
Так четырехугольник EFNM описан около окружности,
а четырехугольник NMКD
не является
описанным около этой окружности.
Если все стороны
многоугольника касаются окружности ,то окружность называется
в п и с а н н о й
в многоугольник ,
а многоугольник –
о п и с а н н ы м
около этой окружности.
E
F
D
K
M
N
Слайд 6
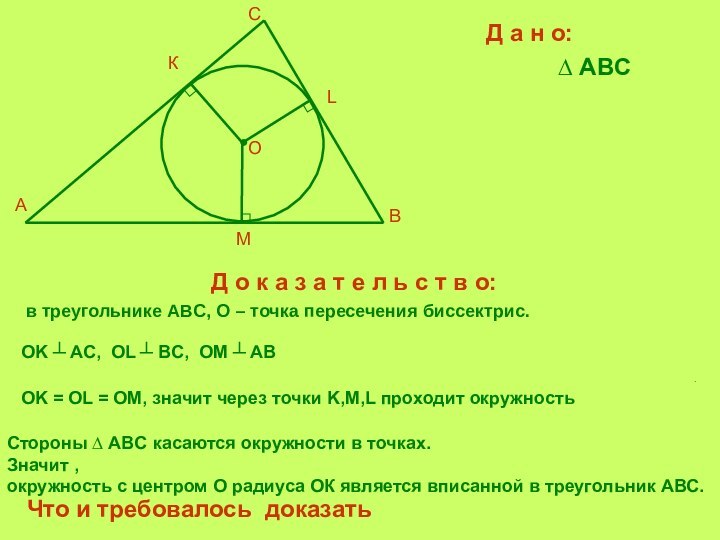
Д а н о:
∆ ABC
Д о к а
з а т е л ь с т в
о:в треугольнике ABC, О – точка пересечения биссектрис.
OK ┴ AС, OL ┴ BC, OM ┴ AB
Стороны ∆ ABC касаются окружности в точках.
Значит ,
окружность с центром О радиуса ОК является вписанной в треугольник АВС.
Что и требовалось доказать
А
В
С
О
К
L
M
OK = OL = OM, значит через точки K,M,L проходит окружность