а стороны пересекают её, называется вписанным.
Вписанный угол
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть






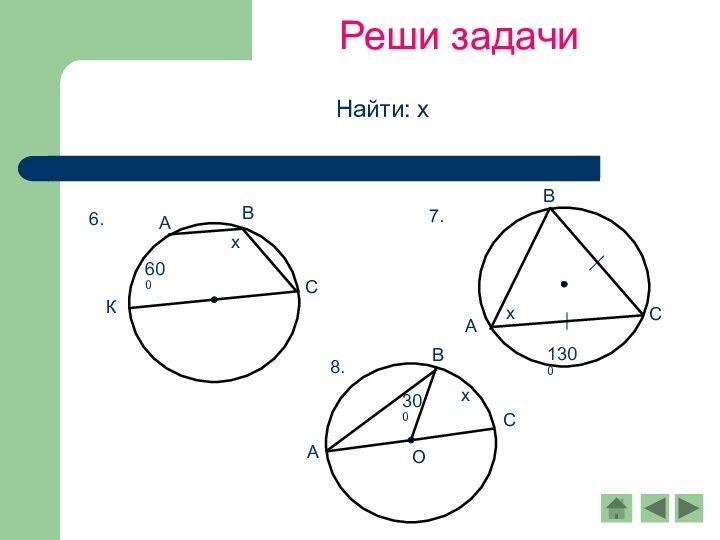



Вписанный угол
Доказательство:
1 случай. ВС проходит через центр окружности.
Проведём ОА. Тогда дуга АС меньше полуокружности.
Доказательство:
2случай. Центр окружности лежит внутри угла АВС.
Проведём луч ВО, который пересекает дугу АС в точке К
Доказательство:
3 случай. Центр окружности лежит вне угла АВС.
Проведём луч ВО, который пересекает Oкр(О;r) в точке К
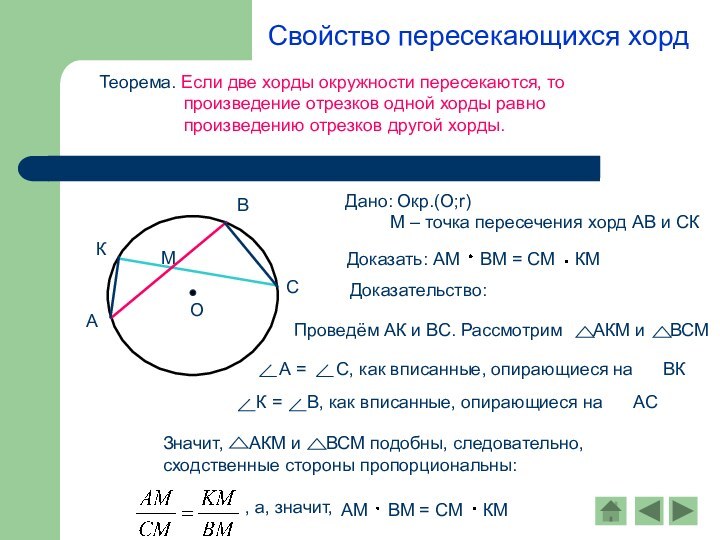
Дано: Окр.(О;r)
М – точка пересечения хорд АВ и СК
Доказательство: