- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Вывод канонических уравнений гиперболы и параболы
Содержание
- 2. Цели и задачиЦели:Рассмотреть основные понятия по теме
- 3. Теоретический материалГиперболой называется кривая, уравнение которой в некоторой прямоугольной системе координат имеет вид:
- 4. Теоретический материалСвойства гиперболы1) Параметры a,
- 5. Теоретический материал3) Координатные оси Ox и Oy
- 6. Теоретический материал Точки
- 7. Теоретический материал6) Гипербола есть множество точек плоскости,
- 8. Теоретический материал7) Оптическое свойство гиперболыЕсли поместить в
- 9. Теоретический материалРавносторонняя гипербола
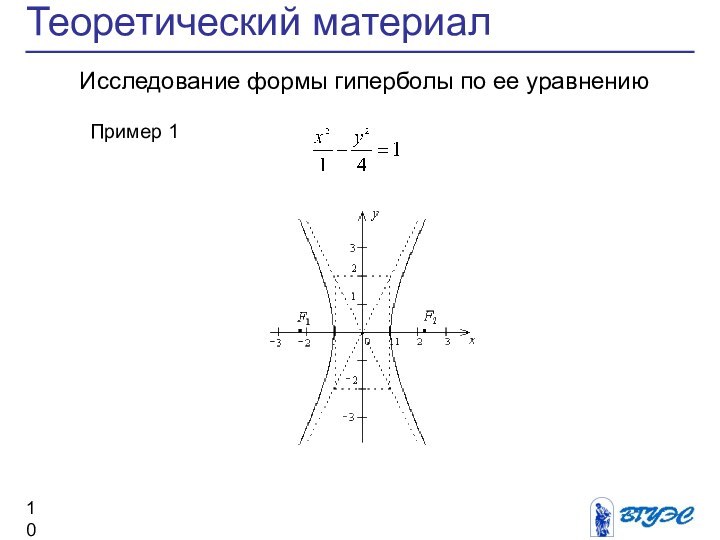
- 10. Теоретический материалИсследование формы гиперболы по ее уравнению
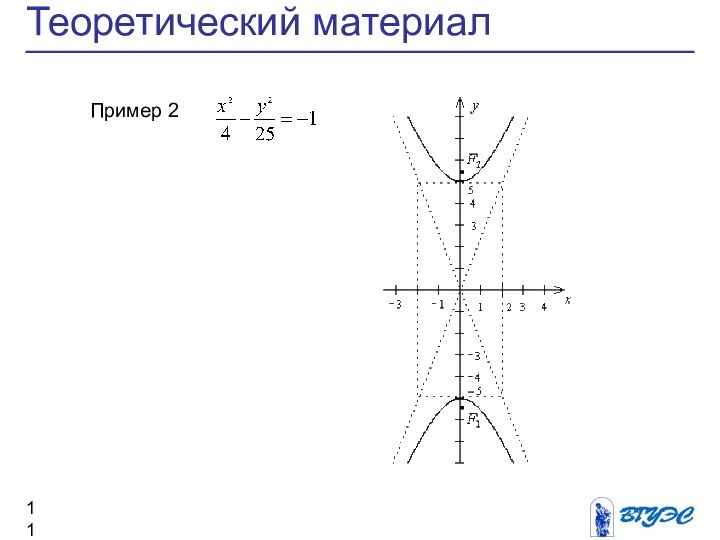
- 11. Теоретический материал Пример 2
- 12. Теоретический материалПараболой называется кривая, уравнение которой в некоторой прямоугольной системе координат имеет вид:
- 13. Теоретический материалСвойства параболы 1) Все точки параболы
- 14. Теоретический материал 4) Парабола есть множество точек,
- 15. Теоретический материал5) Оптическое свойство параболы Если
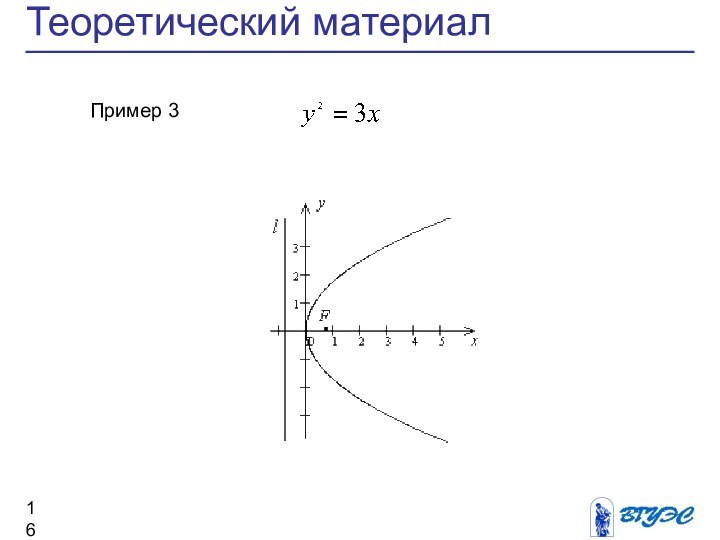
- 16. Теоретический материал Пример 3
- 17. Теоретический материал Пример 4
- 18. Ключевые понятияГиперболаПараболаЭксцентриситетФокусДиректрисаАсимптоты
- 19. Контрольные вопросыОпределение гиперболыСвойства гиперболыЭксцентриситет гиперболыДиректрисы и фокусы
- 20. Скачать презентацию
- 21. Похожие презентации
Цели и задачиЦели:Рассмотреть основные понятия по теме «Вывод канонических уравнений гиперболы и параболы» Задачи:Рассмотреть свойства гиперболы Рассмотреть свойства параболы















Слайд 2
Цели и задачи
Цели:
Рассмотреть основные понятия по теме «Вывод
канонических уравнений гиперболы и параболы»
свойства параболы
Слайд 3
Теоретический материал
Гиперболой называется кривая, уравнение которой в некоторой
прямоугольной системе координат имеет вид:
Слайд 4
Теоретический материал
Свойства гиперболы
1) Параметры a, b
называются соответственно действительной
и мнимой полуосями
гиперболы. Гипербола лежит вне полосы
Вершинами гиперболы являются точки
2) Гипербола лежит в вертикальных углах, образованных
прямыми и содержащих точки оси Ox
Данные прямые называются асимптотами гиперболы
Слайд 5
Теоретический материал
3) Координатные оси Ox и Oy канонической
системы координат
являются осями симметрии гиперболы,
а начало координат – ее центром симметрии
4) На гиперболе лежат точки, сколь угодно далекие от начала
координат
5) Гипербола есть множество точек, абсолютная величина
разности расстояний от которых до двух данных точек (фокусов)
постоянна (равна заданному числу)
Слайд 6
Теоретический материал
Точки
где
называются соответственно правым и левым фокусами гиперболы.
Величина называется фокусным расстоянием.
Слайд 7
Теоретический материал
6) Гипербола есть множество точек плоскости, отношение
расстояний от которых до данной точки (фокуса
гиперболы) и до данной прямой (одноименной с фокусом директрисы)
постоянно (равно эксцентриситету гиперболы)
Число называется эксцентриситетом гиперболы
Правой и левой директрисой гиперболы называются прямые
Слайд 8
Теоретический материал
7) Оптическое свойство гиперболы
Если поместить в один
из фокусов гиперболы с зеркальной
«поверхностью» точечный источник света,
то все лучи после отражения от «поверхности» видятся исходящими из другого фокуса
Гипербола
называется сопряженной к гиперболе
Слайд 9
Теоретический материал
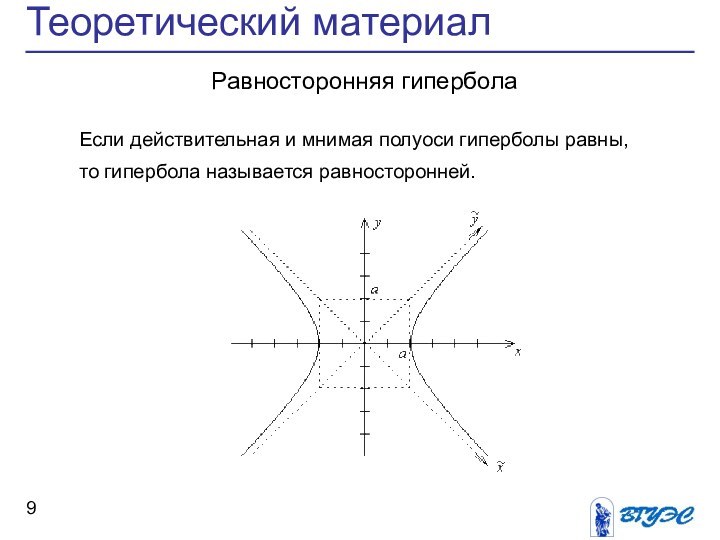
Равносторонняя гипербола
Если действительная и мнимая полуоси гиперболы равны,
то гипербола называется равносторонней.
Слайд 12
Теоретический материал
Параболой называется кривая, уравнение которой в некоторой
прямоугольной системе координат имеет вид:
Слайд 13
Теоретический материал
Свойства параболы
1) Все точки параболы лежат
в правой полуплоскости.
Точка О(0,0) лежит
на параболе и называется ее вершиной.2) На параболе лежат точки, сколь угодно далекие
от начала координат
3) Ось абсцисс канонической координатной системы является
единственной осью симметрии параболы.
Ось симметрии параболы называется осью параболы.
Слайд 14
Теоретический материал
4) Парабола есть множество точек, равноудаленных
от данной
точки (фокуса параболы) и
от данной прямой (директрисы параболы).
Точка - фокус параболы
Прямая - директриса параболы
Слайд 15
Теоретический материал
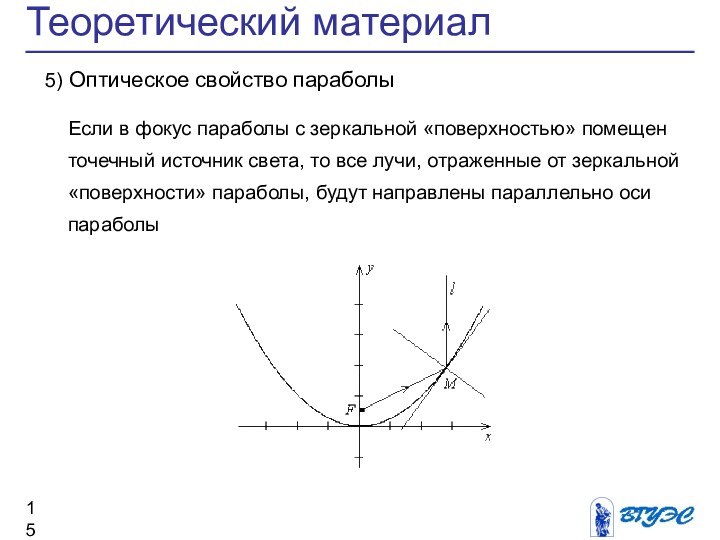
5) Оптическое свойство параболы
Если в
фокус параболы с зеркальной «поверхностью» помещен
точечный
источник света, то все лучи, отраженные от зеркальной «поверхности» параболы, будут направлены параллельно оси
параболы





























