Презентация на тему Взаимное расположение двух прямых

каждый случай.
1. Параллельные прямые линии.
Параллельными называются две прямые, которые лежат

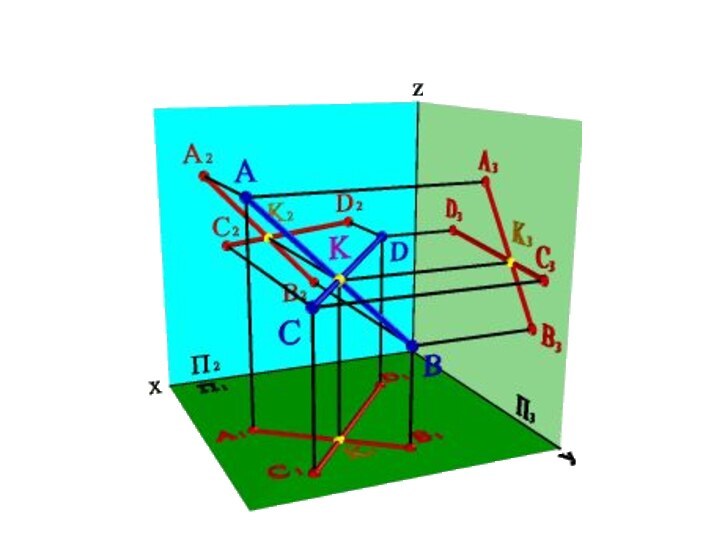
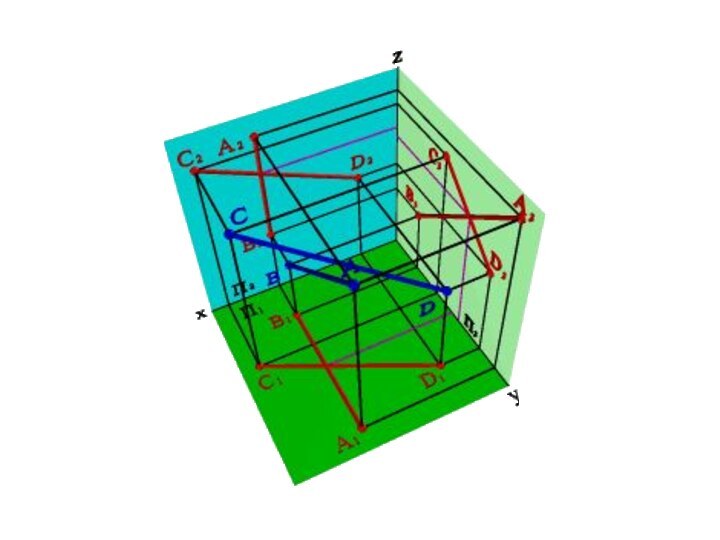
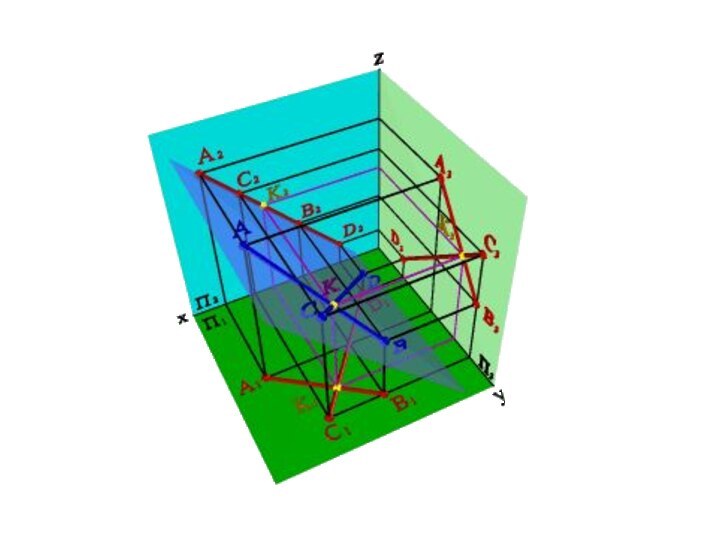
в одной плоскости и не имеют общих точек.
Проекции параллельных прямых на любую плоскость (не перпендикулярную данным прямым) - параллельны. Если AB//CD то A1B1//C1D1; A2B2//C2D2; A3B3//C3D3 (рис.33). В общем случае справедливо и обратное утверждение.

плоскости и имеющие одну общую точку.
Если прямые пересекаются, то

точки пересечения их одноименных проекций находится на одной линии связи (рис. 35).

есть два частных случая:
1. Если одна из прямых параллельна

какой-либо из плоскостей проекций, например, профильной (рис.36), то по двум проекциям невозможно судить об их взаимном расположении. Так горизонтальная и фронтальная проекции отрезков АВ и СД пересекаются, причем точка пересечения проекций лежит на одной линии связи, однако сами отрезки не пересекаются, потому что точка пересечения профильных проекций этих отрезков не лежит на одной линии связи с точками пересечения их горизонтальной и фронтальной проекций.

проецирующей плоскости, например перпендикулярной фронтальной плоскости проекций (рис. 37).
О взаимном

расположении прямых, лежащих в этой плоскости, можно судить по одной горизонтальной проекции (А1В1∩С1D1Þ  АВ∩СD).

одной плоскости.
Если прямые не пересекаются и не параллельны между

собой, то точка пересечения их одноименных проекций не лежит на одной линии связи.
Точке пересечения фронтальных проекций прямых (рис. 38) соответствуют две точки  А и В, из которых одна принадлежит прямой а, другая в. Их фронтальные проекции совпадают лишь потому, что в пространстве обе точки А и Внаходятся на общем перпендикуляре к фронтальной плоскости проекций. Горизонтальная проекция этого перпендикуляра, обозначенная стрелкой, позволяет установить, какая из двух точек ближе к наблюдателю. На предложенном примере ближе точка В, лежащая на прямой в, следовательно, прямая в проходит в этом месте ближе прямой а и  фронтальная проекция точки В закрывает проекцию точки А. (Для точек С и D решение аналогично).
Этот способ определения видимости по конкурирующим точкам. В данном случае  точки А и В- фронтально конкурирующие, а С и D -горизонтально конкурирующие.