- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Взаимное расположение прямой и окружности
Содержание
- 2. Как вы думаете, сколько общих точек могут иметь прямая и окружность?О
- 3. ОСначала вспомним как задаётся окружностьОкружность (О, r)r – радиусrABАВ – хорда СDCD - диаметр
- 4. Исследуем взаимное расположение прямой и окружности в
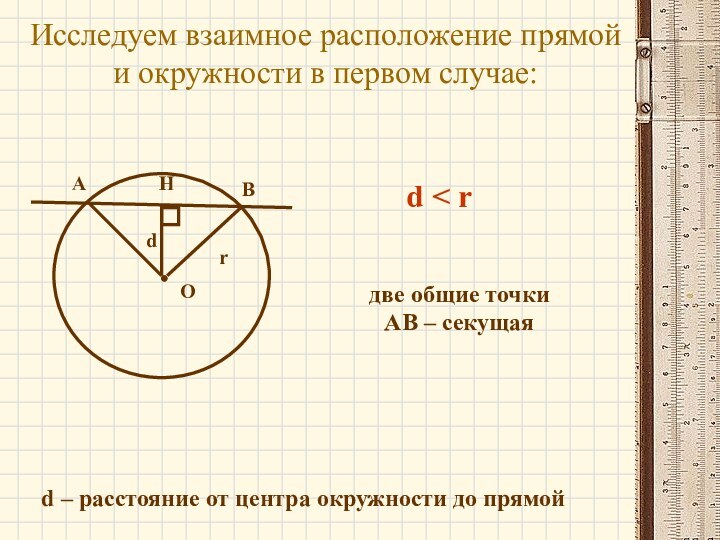
- 5. Второй случай:ОНrодна общая точкаd = rd – расстояние от центра окружности до прямойd
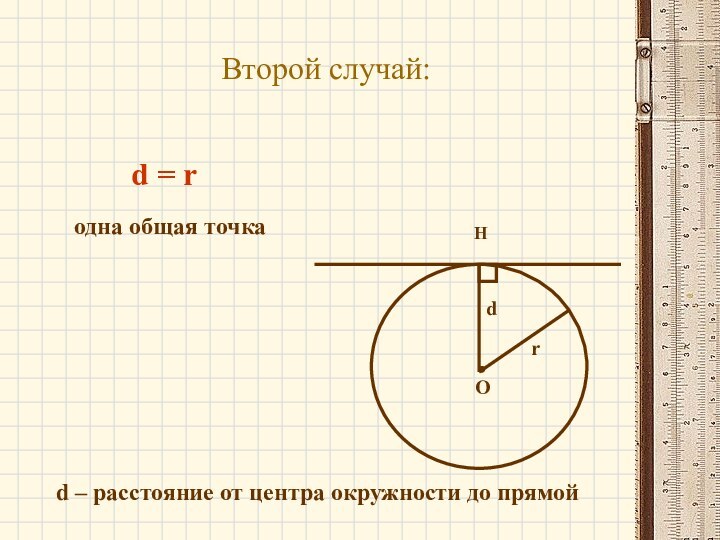
- 6. Третий случай:ОHdrd > rd – расстояние от центра окружности до прямойне имеют общих точек
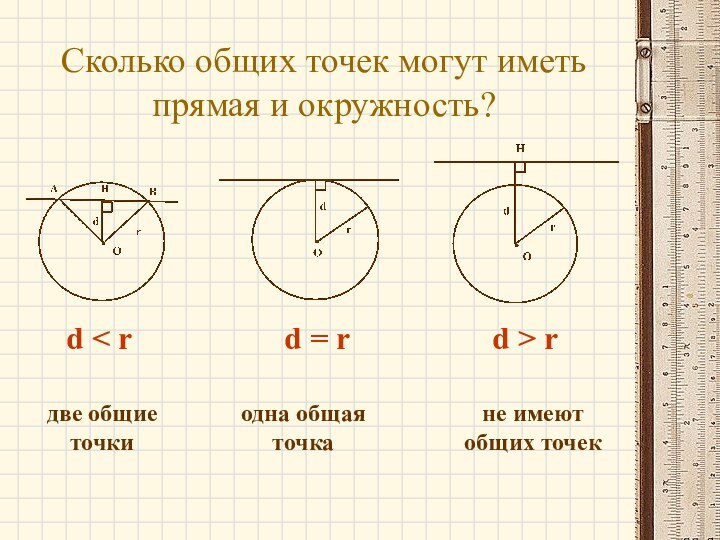
- 7. Сколько общих точек могут иметь прямая и
- 8. Взаимное расположение прямой и окружностиrd = rОкружность
- 9. Свойство касательной.Касательная к окружности перпендикулярна к радиусу, проведенному в точку касания. АВ
- 10. Даны прямоугольник АВСО, диагональ
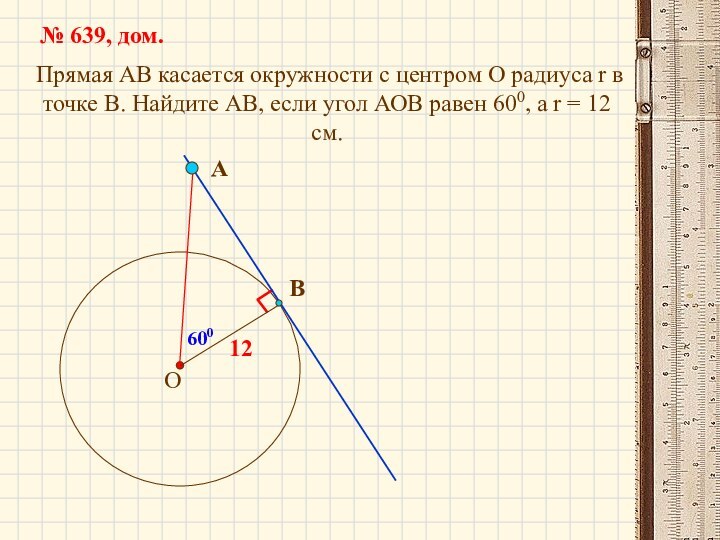
- 13. 600
- 14. 600
- 15. 300
- 16. Прямая АВ касается окружности с центром
- 17. Скачать презентацию
- 18. Похожие презентации
Как вы думаете, сколько общих точек могут иметь прямая и окружность?О



Слайд 3
О
Сначала вспомним как задаётся окружность
Окружность (О, r)
r –
радиус
r
A
B
АВ – хорда
С
D
CD - диаметр
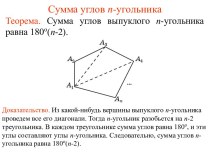
Слайд 4 Исследуем взаимное расположение прямой и окружности в первом
случае:
d – расстояние от центра окружности до прямой
О
А
В
Н
d
rдве общие точки
АВ – секущая
r
d
Слайд 7 Сколько общих точек могут иметь прямая и окружность?
d < r
d = r
d > r
две общие точки
одна
общая точкане имеют общих точек
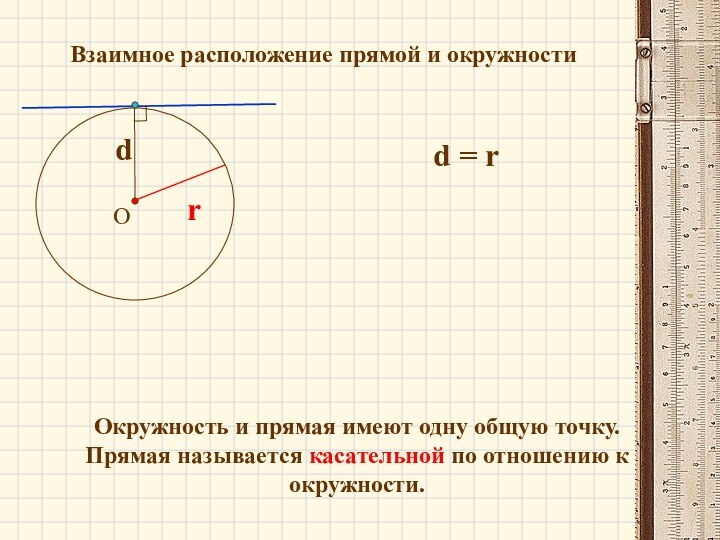
Слайд 8
Взаимное расположение прямой и окружности
r
d = r
Окружность и
прямая имеют одну общую точку.
Прямая называется касательной по отношению
к окружности.
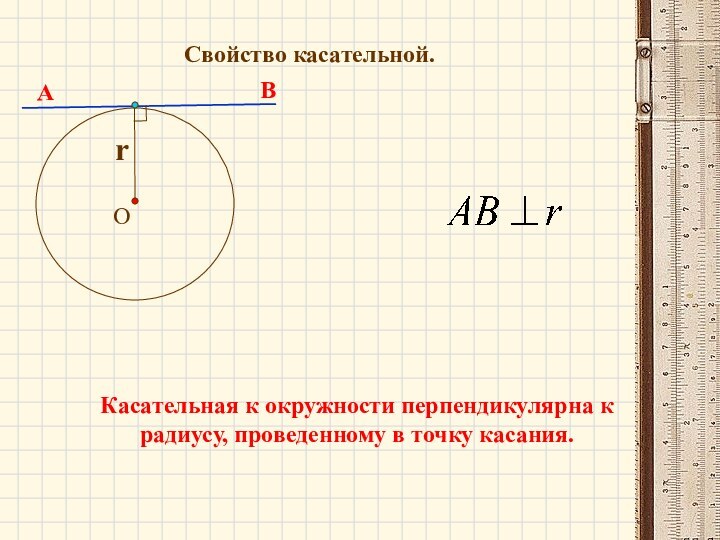
Слайд 9
Свойство касательной.
Касательная к окружности перпендикулярна к радиусу, проведенному
в точку касания.
А
В
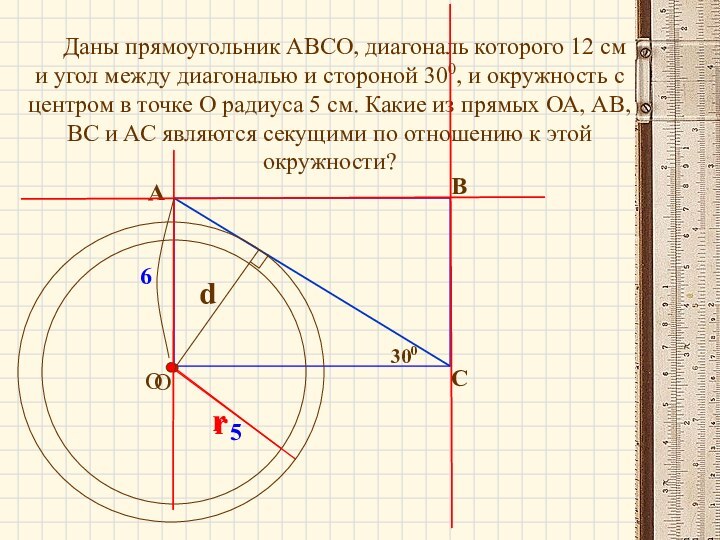
Слайд 10
Даны прямоугольник АВСО, диагональ которого
12 см и угол между диагональю и стороной 300,
и окружность с центром в точке О радиуса 5 см. Какие из прямых ОА, АВ, ВС и АС являются секущими по отношению к этой окружности?А
В
С
5
6
300
Слайд 11
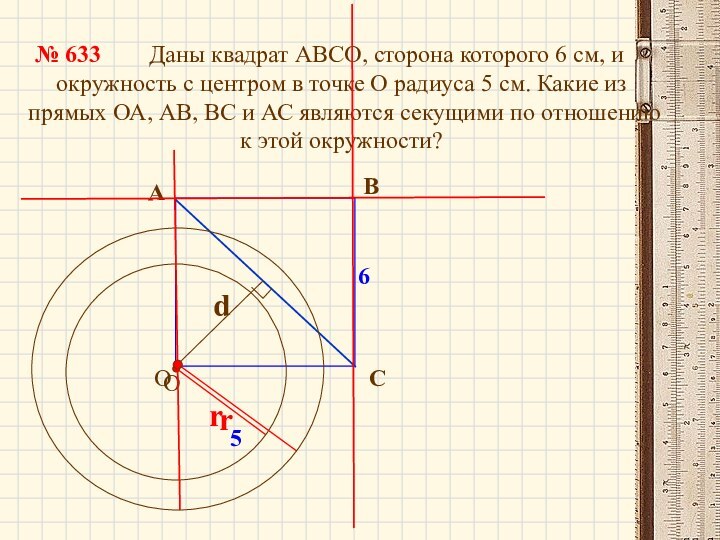
Даны квадрат АВСО, сторона которого 6 см, и
окружность
с центром в точке О радиуса 5 см. Какие из прямых ОА, АВ, ВС и АС являются секущими по отношению к этой окружности?А
В
С
№ 633
5
6
Слайд 12
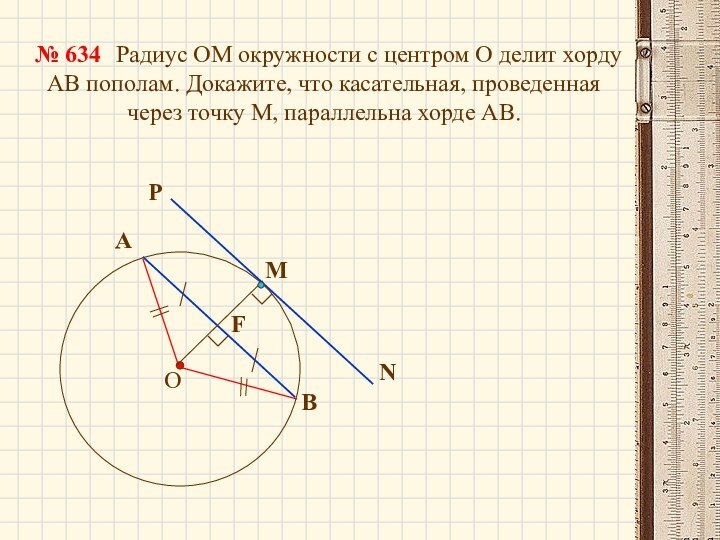
Радиус ОМ окружности с центром О делит хорду АВ
пополам. Докажите, что касательная, проведенная через точку М, параллельна хорде АВ.№ 634
F
Слайд 13
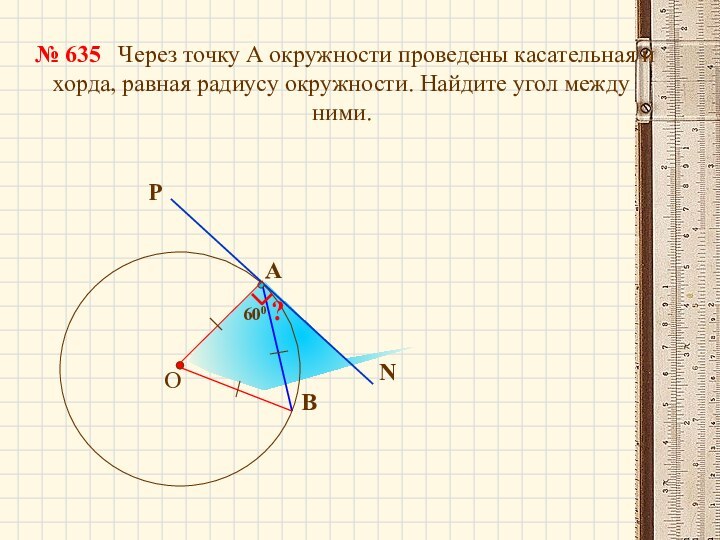
600
Через точку А окружности проведены касательная и хорда, равная
радиусу окружности. Найдите угол между ними.№ 635
?
Слайд 14
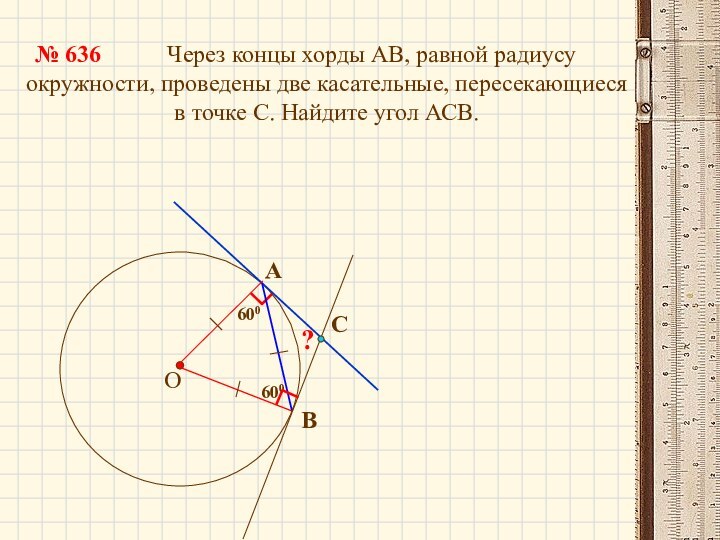
600
Через концы хорды АВ, равной радиусу окружности, проведены две
касательные, пересекающиеся в точке С. Найдите угол АСВ.№ 636
?
600
Слайд 15
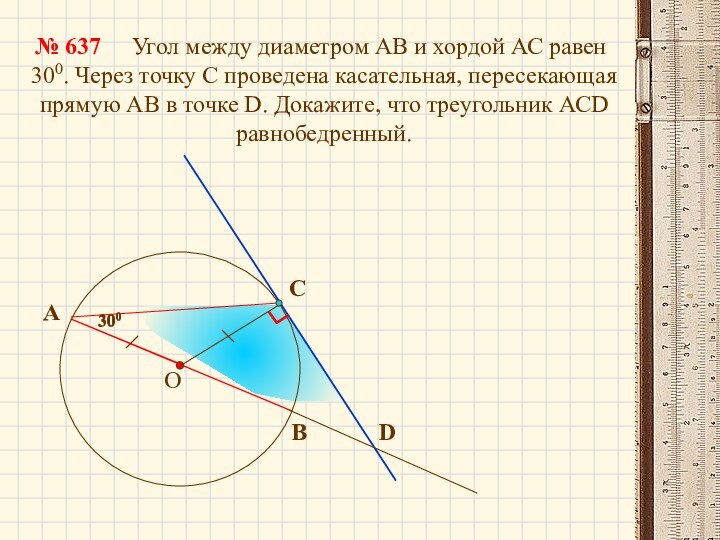
300
Угол между диаметром АВ и хордой АС равен
300. Через точку С проведена касательная, пересекающая прямую АВ в точке D. Докажите, что треугольник АСD равнобедренный.№ 637
300
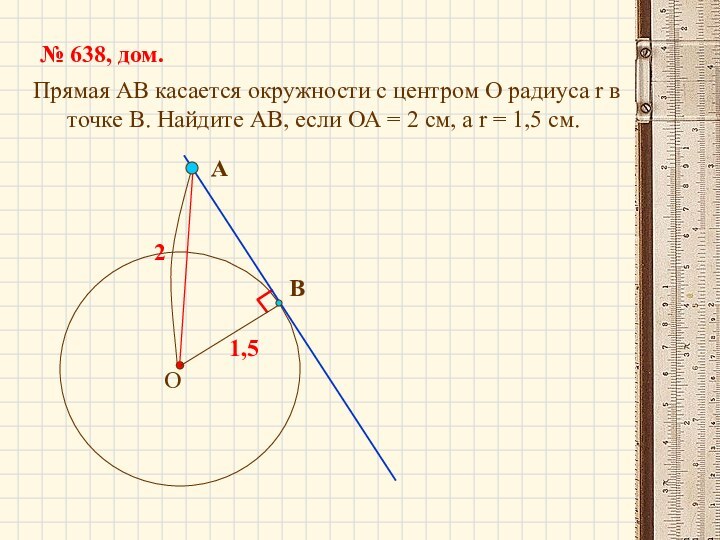
Слайд 16 Прямая АВ касается окружности с центром О
радиуса r в точке В. Найдите АВ, если ОА
= 2 см, а r = 1,5 см.№ 638, дом.
1,5