Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Задачи на взвешивание (материалы для работы в кружке математики) учебно-методический материал по математике (2, 3, 4 класс)

Содержание

2. Задачи на взвешивание тип олимпиадных задач по
3. Взвешиваемые объекты1). Чаще всего монеты.2). Реже имеется
4. «Нестандартные» задачи1). Весы непосредственно показывают массу.2).
5. Состояния весов1). Перевесила левая чаша.2). Перевесила правая чаша.3). Чаши находятся в равновесии.
6. Виды задач на взвешивание1). Требуется определить минимальное
7. Способы оформления решения задач1). Арифметический2). Алгебраический3). Пошаговое описание операций4). Графический5). Метод предположений
8. Задача Среди трех монет одна
9. I способ. Описание операций1). Возьмем две монеты
10. 5). Если перевесила правая чаша весов, Значит,
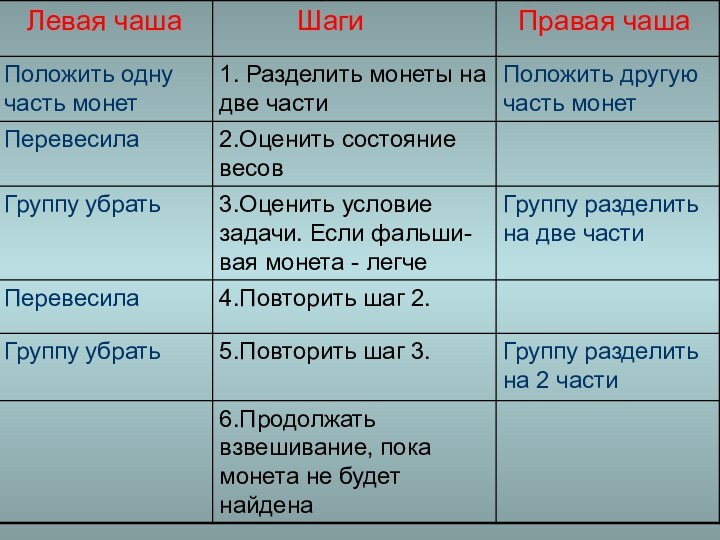
11. II способ. Пошаговое описание действий в таблице
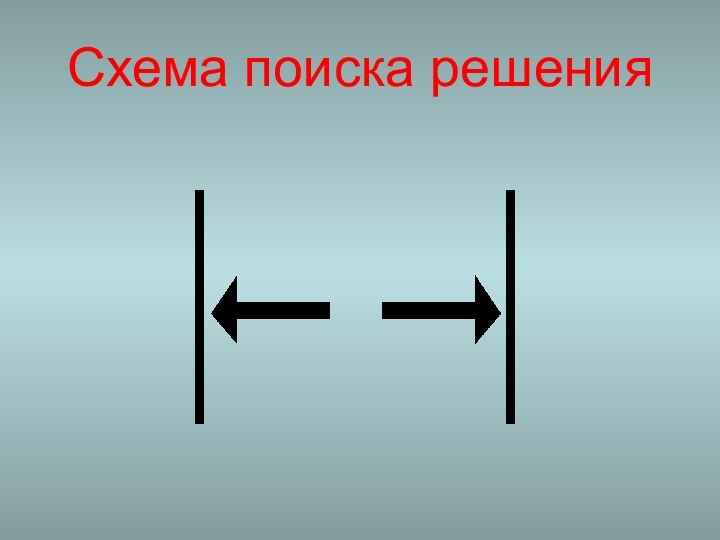
13. Схема поиска решения
14. Блок-схемаНачалоРаздели монеты на две частиПоложи кучки на
15. III способ. Графический1). Пронумеруем монеты.2). Взвесим 1
16. Задача На одной чаше весов арбуз
17. Способы решения задачи 1). Арифметический1). 3+1=4(кг) –
18. 2). Алгебраический:Пусть х (кг) – масса арбуза.Тогда
19. 3). Метод предположений:1). Допустим, что масса арбуза
20. Задачи на взвешивание Это увлекательно!
21. Потренируйся!1). Геологи нашли 7 камней, массы которых
22. Потренируйся!6). Имеется 9 одинаковых по виду шариков.
23. Потренируйся!11). В мешке 24 кг гвоздей. Как
24. Скачать презентацию
25. Похожие презентации

Задачи на взвешивание тип олимпиадных задач по математике, в которых требуется установить тот или иной факт посредством взвешивания на рычажных весах без циферблата.

Главная
Математика
Задачи на взвешивание (материалы для работы в кружке математики) учебно-методический материал по математике (2, 3, 4 класс)

Задачи на взвешиваниеПрезентацию выполнила:Парадовская Елена Александровна учитель начальных классов МОУ «СОШ №21 с УИОП»г.Ухта

Задачи на взвешивание тип олимпиадных задач по математике, в которых требуется установить

Взвешиваемые объекты1). Чаще всего монеты.2). Реже имеется набор гирек известной массы.3). Могут

«Нестандартные» задачи1). Весы непосредственно показывают массу.2). Рычажные весы с циферблатом,

Состояния весов1). Перевесила левая чаша.2). Перевесила правая чаша.3). Чаши находятся в равновесии.

Виды задач на взвешивание1). Требуется определить минимальное число взвешиваний.2). Привести алгоритм определения

Способы оформления решения задач1). Арифметический2). Алгебраический3). Пошаговое описание операций4). Графический5). Метод предположений

Задача Среди трех монет одна фальшивая. Как с помощью чашечных

I способ. Описание операций1). Возьмем две монеты из трех. Назовем их 1-я

5). Если перевесила правая чаша весов, Значит, 2-я монета тяжелее, но пока

II способ. Пошаговое описание действий в таблице

Задачи на взвешивание (материалы для работы в кружке математики) учебно-методический материал по математике (2, 3, 4 класс)

Блок-схемаНачалоРаздели монеты на две частиПоложи кучки на разные чаши весовВесы в равновесииДаФальшивая

III способ. Графический1). Пронумеруем монеты.2). Взвесим 1 и 2 монеты (по одной

Задача На одной чаше весов арбуз и гири в 3 кг

Способы решения задачи 1). Арифметический1). 3+1=4(кг) – масса двух гирь на чаше

2). Алгебраический:Пусть х (кг) – масса арбуза.Тогда (х+3+1) кг – масса левой

3). Метод предположений:1). Допустим, что масса арбуза 1 кг. Тогда 1+3+1=5 (кг)

Потренируйся!1). Геологи нашли 7 камней, массы которых 1 кг, 2 кг, 3

Потренируйся!6). Имеется 9 одинаковых по виду шариков. 8 из них имеют одинаковую

Потренируйся!11). В мешке 24 кг гвоздей. Как на чашечных весах без гирь

Использованная литература:1). Левитас Г.Г. Нестандартные задачи на уровах математики. – М.: Илекса,

Слайды презентации

Слайд 2 Задачи на взвешивание
тип олимпиадных задач по математике,

Задачи на взвешивание тип олимпиадных задач по математике, в которых требуется

в которых требуется установить тот или
иной факт посредством

взвешивания на рычажных весах без циферблата.

Слайд 3 Взвешиваемые объекты
1). Чаще всего монеты.
2). Реже имеется набор

Взвешиваемые объекты1). Чаще всего монеты.2). Реже имеется набор гирек известной массы.3).

гирек известной массы.
3). Могут быть шары, различные предметы (одушевленные

и неодушевленные).

Слайд 4 «Нестандартные» задачи
1). Весы непосредственно показывают массу.
2). Рычажные

«Нестандартные» задачи1). Весы непосредственно показывают массу.2). Рычажные весы с циферблатом, показывающим

весы
с циферблатом, показывающим разность веса грузов на

чашах.
3). Фигурирует безмен.
4). Фигурируют неравноплечие весы.

Слайд 5 Состояния весов
1). Перевесила левая чаша.

2). Перевесила правая чаша.

3).

Чаши находятся в равновесии.

Слайд 6 Виды задач на взвешивание
1). Требуется определить минимальное число

Виды задач на взвешивание1). Требуется определить минимальное число взвешиваний.2). Привести алгоритм

взвешиваний.
2). Привести алгоритм определения факта за данное количество взвешиваний.
3).

Выявить возможность установления факта за некоторое количество взвешиваний.

Слайд 7 Способы оформления решения задач
1). Арифметический
2). Алгебраический
3). Пошаговое описание

операций
4). Графический
5). Метод предположений

Слайд 8 Задача
Среди трех монет одна фальшивая.

Как с помощью чашечных весов без гирь найти фальшивую

монету?

Слайд 9 I способ. Описание операций
1). Возьмем две монеты из

I способ. Описание операций1). Возьмем две монеты из трех. Назовем их

трех. Назовем их 1-я и 2-я.
2). Положим 1-ю монету

на левую чашу весов, а 2-ю на правую чашу.
3). Если весы уравновесились, то 1-я и 2-я монеты одинаковые, значит, настоящие. Таким образом, фальшивая монета – 3-я.
4). Повторим 1-ю и 2-ю операции.

Слайд 10 5). Если перевесила правая чаша весов, Значит, 2-я

5). Если перевесила правая чаша весов, Значит, 2-я монета тяжелее, но

монета тяжелее, но пока неизвестно, которая фальшивая.

6). Вместо 1-й

монеты положим на левую чашу весов 3-ю монету. Если весы в равновесии, то фальшивая монета – 1-я (она легче).
7). Если весы не в равновесии, надо сравнить 1-ю и 3-ю монеты.

Слайд 11 II способ. Пошаговое описание действий в таблице

Слайд 12

Слайд 13 Схема поиска решения

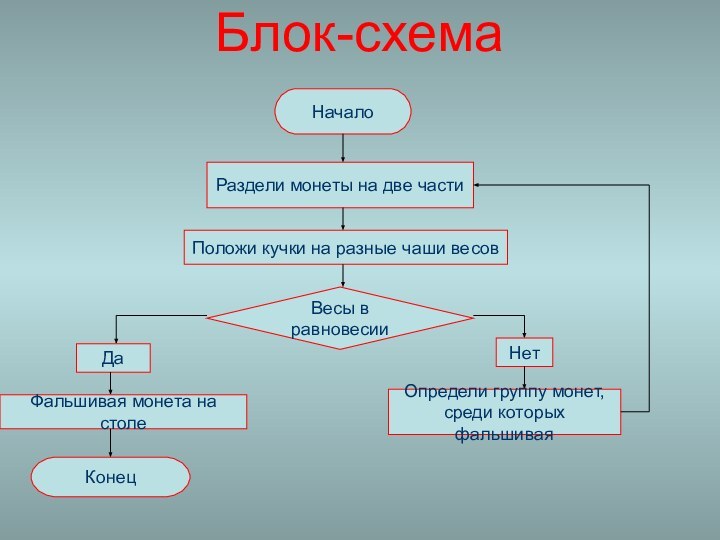
Слайд 14 Блок-схема
Начало
Раздели монеты на две части
Положи кучки на разные

Блок-схемаНачалоРаздели монеты на две частиПоложи кучки на разные чаши весовВесы в

чаши весов
Весы в равновесии
Да
Фальшивая монета на столе
Нет
Определи группу монет,

среди которых фальшивая

Конец

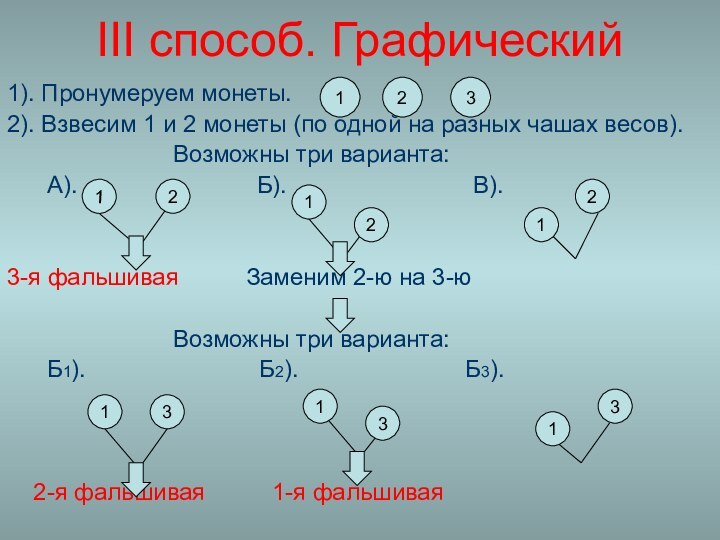
Слайд 15 III способ. Графический
1). Пронумеруем монеты.
2). Взвесим 1 и

III способ. Графический1). Пронумеруем монеты.2). Взвесим 1 и 2 монеты (по

2 монеты (по одной на разных чашах весов).

Возможны три варианта:
А). Б). В).

3-я фальшивая Заменим 2-ю на 3-ю

Возможны три варианта:
Б1). Б2). Б3).

2-я фальшивая 1-я фальшивая

Слайд 16 Задача
На одной чаше весов арбуз и

гири в 3 кг и в 1 кг. На

другой чаше весов – гиря в 10 кг. Весы находятся в равновесии. Какова масса арбуза?

Слайд 17 Способы решения задачи

1). Арифметический
1). 3+1=4(кг) – масса

Способы решения задачи 1). Арифметический1). 3+1=4(кг) – масса двух гирь на

двух гирь на чаше весов с арбузом.

2). 10-4=6(кг) –

масса арбуза.

Ответ: 6 кг.

Слайд 18 2). Алгебраический:
Пусть х (кг) – масса арбуза.
Тогда (х+3+1)

2). Алгебраический:Пусть х (кг) – масса арбуза.Тогда (х+3+1) кг – масса

кг – масса левой чаши весов.
10 кг – масса

правой чаши весов.
Весы находятся в равновесии.
х+3+1=10
х+4=10
х=10-4
х=6
6 (кг) – масса арбуза.

Слайд 19 3). Метод предположений:
1). Допустим, что масса арбуза 1

3). Метод предположений:1). Допустим, что масса арбуза 1 кг. Тогда 1+3+1=5

кг. Тогда 1+3+1=5 (кг) – масса на левой чаше.

5 < 10, что не соответствует условию. Значит, масса арбуза не 1 кг.

2). Допустим, что масса арбуза 2 кг. Тогда 2+3+1=6 (кг) – масса на левой чаше. 6 < 10, что не соответствует условию. Значит, масса арбуза не 2 кг.

3). Допустим, что масса арбуза 3 кг. Тогда 3+3+1=7 (кг) – масса на левой чаше. 7 < 10, что не соответствует условию. Значит, масса арбуза не 3 кг.

4). Допустим, что масса арбуза 4 кг. Тогда 4+3+1=8 (кг) – масса на левой чаше. 8 < 10, что не соответствует условию. Значит, масса арбуза не 4 кг.

5). Допустим, что масса арбуза 5 кг. Тогда 5+3+1=9 (кг) – масса на левой чаше. 9 < 10, что не соответствует условию. Значит, масса арбуза не 5 кг.

6). Допустим, что масса арбуза 6 кг. Тогда 6+3+1=10 (кг) – масса на левой чаше. 10 = 10, что соответствует условию. Значит, масса арбуза 6 кг.

Ответ: 6 кг.

Слайд 20 Задачи на взвешивание
Это увлекательно!

Слайд 21 Потренируйся!
1). Геологи нашли 7 камней, массы которых 1

Потренируйся!1). Геологи нашли 7 камней, массы которых 1 кг, 2 кг,

кг, 2 кг, 3 кг, 4 кг, 5 кг,

6 кг, 7 кг. Они разложили их в рюкзаки так, что в каждом из рюкзаков масса камней была одинакова. Как это сделали?
2). Из 7 монет 1 – фальшивая (более лёгкая). Как при помощи 2 взвешиваний на чашечных весах определить, какая монета фальшивая?
3). Из восьми внешне одинаковых монет одна фальшивая, она легче. Как определить фальшивую монету на весах без гирь не более чем двумя взвешиваниями?
4). Каким наименьшим числом взвешиваний на чашечных весах без гирь можно найти среди 16 одинаковых по виду монет одну фальшивую (более лёгкую)?
5). Среди экспонатов музея есть 27 одинаковых по виду серебряных монет, но одна из них фальшивая (более тяжёлая). За какое наименьшее количество взвешиваний на чашечных весах без гирь эксперт сможет найти эту монету? Сколько взвешиваний придётся выполнить при самом неблагоприятном стечении обстоятельств?

Слайд 22 Потренируйся!
6). Имеется 9 одинаковых по виду шариков. 8

Потренируйся!6). Имеется 9 одинаковых по виду шариков. 8 из них имеют

из них имеют одинаковую массу, а один – меньшую.

Как на чашечных весах без гирь найти этот шарик?
7). На одной чаше весов 2 куска мыла, а на другой лежат 3/2 такого же куска и ещё гиря в 50 граммов. Весы находятся в равновесии. Какова масса куска мыла?
8). На одну чашу весов положили круг сыра, а на другую чашу 3/4 такого же круга и ещё килограммовую гирю. Установилось равновесие. Сколько весит круг сыра?
9). Четырёх кошек взвесили попарно во всех возможных комбинациях. Получились веса: 7 кг, 8 кг, 9 кг, 10 кг, 11 кг, 12 кг. Найдите общий вес всех четырёх кошек.
10). Есть 10 мешков с золотом. В каждом по 10 монет. В девяти мешках монеты настоящие, а в одном – все фальшивые. Одна настоящая монета весит 5 грамм, а фальшивая – 4 грамма. Имеются весы, показывающие вес в граммах. Необходимо за одно взвешивание точно определить, в каком мешке фальшивые монеты. (Мешки можно раскрывать и вытаскивать монеты).

В мешке 24 кг гвоздей. Как на чашечных весах без гирь и без стрелки отмерить 9 кг гвоздей?

Слайд 23 Потренируйся!
11). В мешке 24 кг гвоздей. Как на

Потренируйся!11). В мешке 24 кг гвоздей. Как на чашечных весах без

чашечных весах без гирь и без стрелки отмерить 9

кг гвоздей?
12). На одной чаше весов арбуз и гири в 3 кг и в 1 кг. На другой чаше весов – гиря в 10 кг. Весы находятся в равновесии. Какова масса арбуза?
13). Какой вес можно взвесить гирями 1 кг, 2 кг и 4 кг на чашечных весах, если гири можно класть только на одну чашу весов?
14). Какую массу можно взвесить гирями 1, 3 и 9 кг, если гири можно класть на обе чаши весов?
15). На чашечных весах взвесили мандарин и яблоко. При первом взвешивании на одну чашу весов положили мандарин, а на другую – две гири по 50 г. При втором взвешивании на одну чашу весов положили яблоко, а на другую – мандарин и гирю в 300 г. Какова масса мандарина и какова масса яблока?