- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Задачи нетрадиционного содержания, решаемые с помощью теоремы Пифагора
Содержание
- 2. ВведениеТеорема Пифагора применяется очень широко. Мы
- 3. Задача 1.Мальчику Вите требуется измерить ширину пруда.
- 4. Дано: расстояние от точки R до точки
- 5. Задача 2.В древней Индии был обычай предлагать
- 6. Выполним чертёж к задаче и обозначим глубину
- 7. Задача 3.На берегу реки рос тополь одинокий.
- 8. Решение: Пусть CD-высота ствола. BD=AB По теореме Пифагора имеем: AB=5 CD=3+5=8Ответ: 8 футов
- 9. Задача 4.Какую наибольшую высоту должна иметь телевизионная
- 10. Задача 5.Используя приведённые ниже данные о длинах
- 11. Решение:a) Необходимо проверить, равна ли сумма квадратов
- 12. Задача 6.Длина стремянки в сложенном виде равно
- 13. Скачать презентацию
- 14. Похожие презентации
ВведениеТеорема Пифагора применяется очень широко. Мы уже узнали о различных способах её доказательства, а так же о жизни самого математика. Теперь давайте рассмотрим, как теорема Пифагора может применяться в решении задач.








Слайд 3
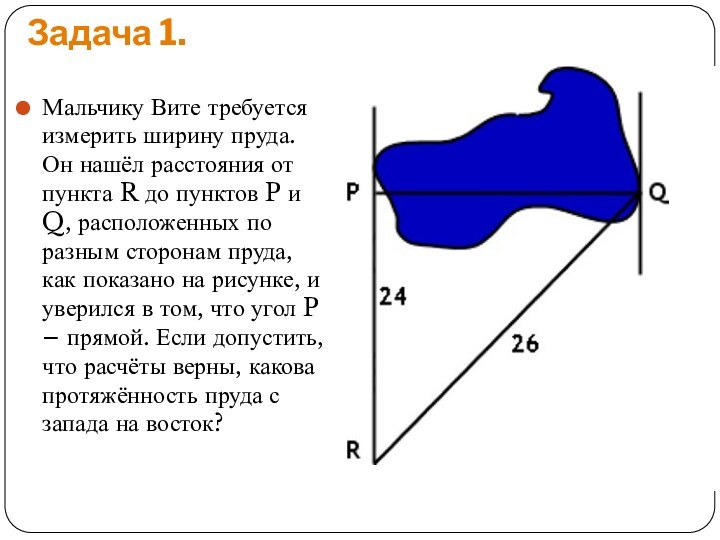
Задача 1.
Мальчику Вите требуется измерить ширину пруда. Он
нашёл расстояния от пункта R до пунктов P и
Q, расположенных по разным сторонам пруда, как показано на рисунке, и уверился в том, что угол P – прямой. Если допустить, что расчёты верны, какова протяжённость пруда с запада на восток?Слайд 4 Дано: расстояние от точки R до точки P
(катет треугольника) равняется 24, от точки R до точки
Q (гипотенуза) – 26.Решение: Поскольку стороны треугольника, изображённого на рисунке, предположительно образуют прямоугольный треугольник, для нахождения длины третьей стороны можно использовать теорему Пифагора:
Выходит ширина пруда составляет 10 метров.
Слайд 5
Задача 2.
В древней Индии был обычай предлагать задачи
в стихах. Я предлагаю вам решить одну из таких
задач.Над озером тихим,
С полфута размером,
высился лотоса цвет.
Он рос одиноко. И ветер порывом
Отнес его в сторону. Нет
Больше цветка над водой.
Нашел же рыбак его ранней весной
В двух футах от места, где рос.
Итак, предложу я вопрос:
Как озера вода глубока.?
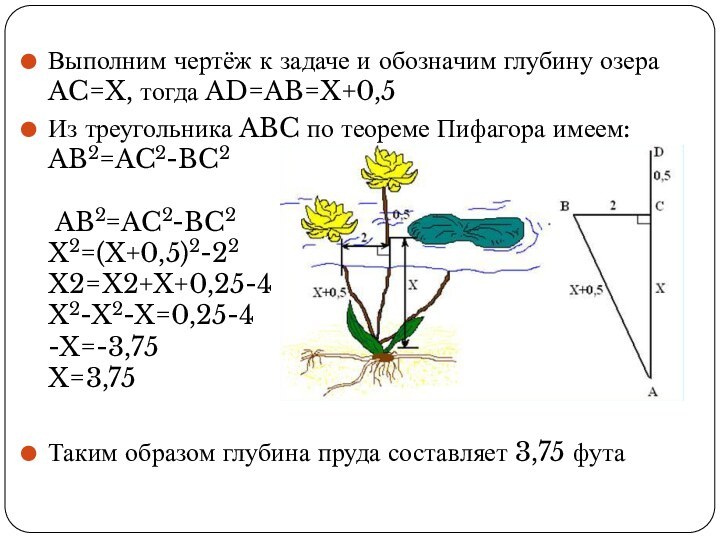
Слайд 6 Выполним чертёж к задаче и обозначим глубину озера
AC=X, тогда AD=AB=X+0,5
Из треугольника ABC по теореме Пифагора имеем:
AB2=AC2-BC2
AB2=AC2-BC2
X2=(X+0,5)2-22
X2=X2+X+0,25-4
X2-X2-X=0,25-4
-X=-3,75
X=3,75Таким образом глубина пруда составляет 3,75 фута
Слайд 7
Задача 3.
На берегу реки рос тополь одинокий.
Вдруг ветра
порыв его ствол надломал. Бедный тополь упал. Угол прямой С течением
реки его ствол составлял. Запомни теперь, что в том месте река В четыре лишь фута была широка. Оказалось три фута всего от ствола. Прошу тебя, мне поскорее скажи: У тополя как велика высота?
Слайд 8
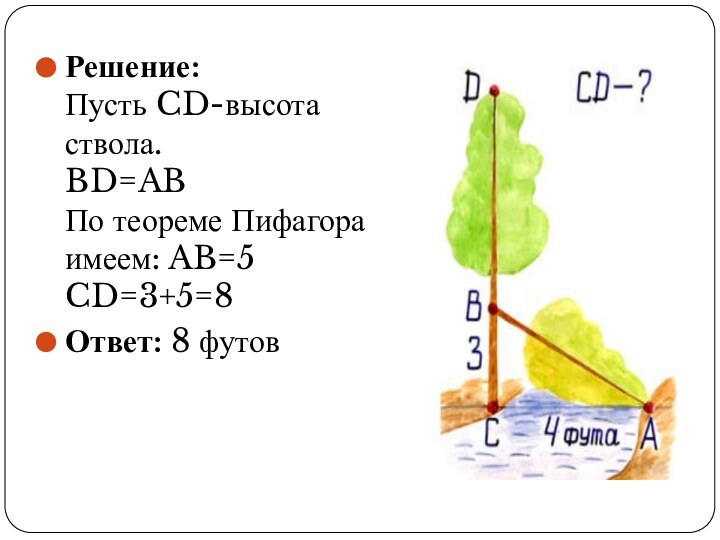
Решение:
Пусть CD-высота ствола.
BD=AB
По теореме Пифагора имеем: AB=5
CD=3+5=8
Ответ: 8
футов
Слайд 9
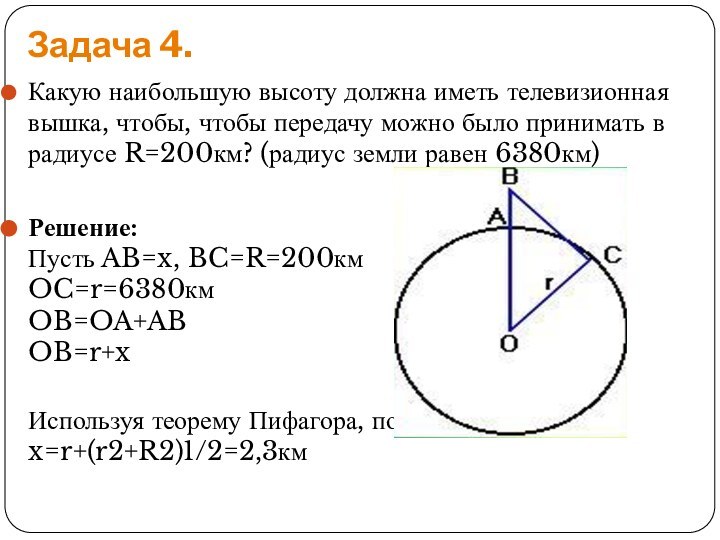
Задача 4.
Какую наибольшую высоту должна иметь телевизионная вышка,
чтобы, чтобы передачу можно было принимать в радиусе R=200км?
(радиус земли равен 6380км)Решение: Пусть AB=x, BC=R=200км OC=r=6380км OB=OA+AB OB=r+x
Используя теорему Пифагора, получим: x=r+(r2+R2)1/2=2,3км
Слайд 10
Задача 5.
Используя приведённые ниже данные о длинах сторон
треугольников, определите, являются ли они прямоугольными.
Дано:
Длины
меньших сторон треугольника равны 45 и 55
соответственно, большей – 75.Длины меньших сторон треугольника равны 28 и 45 соответственно, большей – 5
Слайд 11
Решение:
a) Необходимо проверить, равна ли сумма квадратов длин
меньших
сторон данного треугольника квадрату длины большей:
752= 5625
452+ 552 = 2025
+ 3025 = 50505625 ≠ 5050
Следовательно, первый треугольник не является прямоугольным.
b) Выполняется та же самая операция:
532= 2809
282+ 452 = 784 + 2025 = 2809
2809 = 2809
Следовательно, второй треугольник является прямоугольным.
Слайд 12
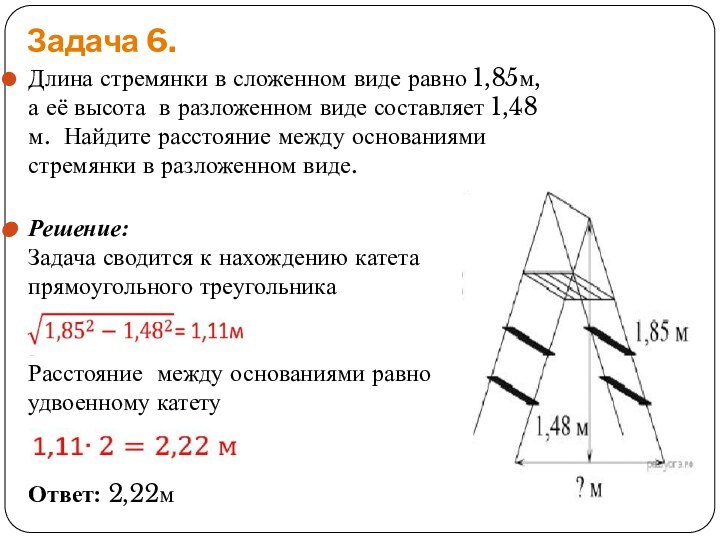
Задача 6.
Длина стремянки в сложенном виде равно 1,85м,
а её высота в разложенном виде составляет 1,48м. Найдите
расстояние между основаниями стремянки в разложенном виде.Решение: Задача сводится к нахождению катета прямоугольного треугольника Расстояние между основаниями равно удвоенному катету
Ответ: 2,22м





























