- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему ПРАКТИЧЕСКИЕ СПОСОБЫ ВЫЧИСЛЕНИЯ ПЛОЩАДИ КРУГА
Содержание
- 2. Умение видеть закономерности настолько ценится, что ни
- 3. Примеры числовых последовательностейЧисловая последовательность – это упорядоченный
- 4. закономерность числовой последовательностиОднако, бывают случаи неоднозначности закона
- 5. Последовательность простых чиселОднако, закон построения последовательности простых
- 6. Некоторые удивительные последовательности
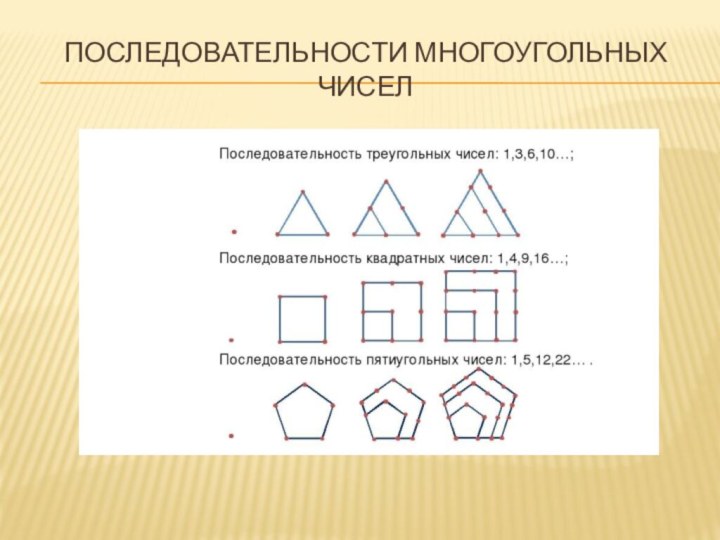
- 7. Последовательности Многоугольных чисел
- 8. Последовательность совершенных чисел 6, 28,
- 9. Последовательность чисел фибоначчи Эта числовая
- 10. Почему именно это животное вошло в историю
- 11. Легенда о создателе шахматВсего зерен 18 446 744
- 12. Последовательности вокруг нас
- 13. задание из рабочей тетради и.ф. ШарыгинаЗадание состояло
- 14. Последовательности в орнаментах
- 15. мелодия – это последовательность?!
- 16. Если мелодия – это последовательность звуков, то верно ли обратное?!
- 17. задачи на последовательности
- 18. Даны две последовательности: 2,4,8,16,14,10,2,4,… и 3,6,12,6,12,… В
- 19. Посчитать сумму чисел 1+2+3+…+99+100
- 20. При хранении бревен их укладывают, как показано
- 21. Вместо эпилога…
- 22. - это способ запоминания цифровой информации поиском
- 23. Скачать презентацию
- 24. Похожие презентации

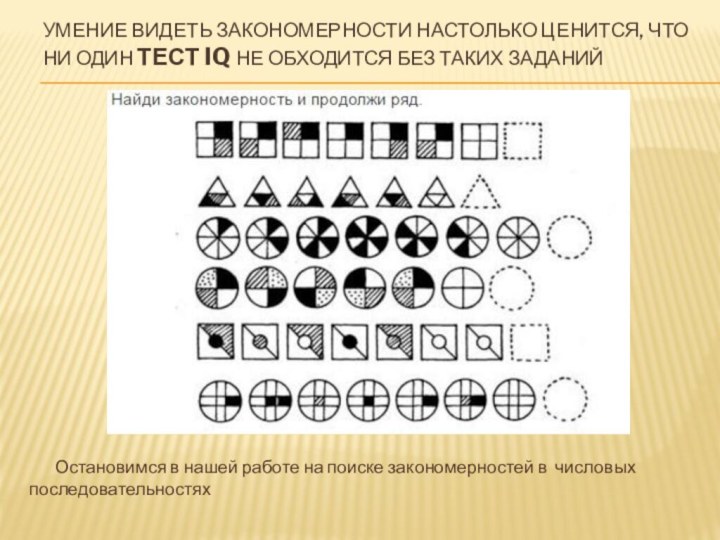


















Слайд 2 Умение видеть закономерности настолько ценится, что ни один
тест IQ не обходится без таких заданий
Остановимся в нашей работе на поиске закономерностей в числовых последовательностях
Слайд 3
Примеры числовых последовательностей
Числовая последовательность – это упорядоченный набор
чисел.
Остановимся на знакомстве с последовательностями, состоящими из натуральных
чисел.1,2,3,4,5,6,7,8,9,10… последовательность натуральных чисел
2,4,6,8,10,12,14… последовательность четных чисел
1,3,5,7,9,11,13,15… последовательность нечетных чисел
1,2,4,8,16,32,64…
0,1,0,1,0,1,0,1…
57, 57,57, 57, 57…
2,0,1,8,2,0,1,8,2…
2018, 2017, 2016, 2015…убывающая последовательность
Существуют и конечные последовательности:
1,2,3,4,5,6,7,8,9 последовательность однозначных чисел
3,4,5 стороны прямоугольного треугольника
Слайд 4
закономерность числовой последовательности
Однако, бывают случаи неоднозначности закона построения
последовательности.
Например, 1, 2, 4… (8? или 7?)
Какое число стоит дальше? 8? Да, то есть каждый предыдущий в 2 раза больше следующего. А может 7? Тоже верно. Если смотреть разницу между соседними элементами. 2-1=1, 4-2=2, ?-4=3! Нам удалось и выявить 2 закономерности, возможно, можно найти и больше… Создайте последовательность, которая соответствует нескольким закономерностям.
Попробуйте, наоборот, записать несколько последовательностей, подчиненных одному закону.
Удивительно, если удалось найти «закон» построения последовательности, то можно предсказать все будущие числа последовательности!
Есть мнение, что для любой последовательности можно найти закономерность.
Слайд 5
Последовательность простых чисел
Однако, закон построения последовательности простых чисел
до сих пор не найден…
Попробуйте, может у вас получится постичь порядок и закономерности их расположения, может,Вы разгадаете их тайну… Натуральное число, отличное от 1,называется простым, если оно делится только на себя и 1. Например, 2, 3, 5, 7, 11, …
Слайд 8
Последовательность совершенных чисел
6, 28, 496,
8128, 33550336, 8589869056, 137438691328, 2305843008139952128
Совершенные
числа равны сумме своих делителей:1-ое совершенное число — 6 имеет следующие собственные делители: 1, 2, 3; их сумма 1 + 2 + 3 = 6.
2-ое совершенное число — 28 имеет следующие собственные делители: 1, 2, 4, 7, 14; их сумма 1 + 2 + 4 + 7 + 14 = 28.
3-ое совершенное число — 496 имеет следующие собственные делители: 1, 2, 4, 8, 16, 31, 62, 124, 248; их сумма 1 + 2 + 4 + 8 + 16 + 31 + 62 + 124 + 248 = 496.
и т.д.
Все чётные совершенные числа являются треугольными числами или шестиугольными числами.
Нечётных совершенных чисел до сих пор не обнаружено, однако, не доказано и то, что их не существует.
Неизвестно также, сколько всего совершенных чисел.
Слайд 9
Последовательность чисел фибоначчи
Эта числовая последовательность
была получена Фибоначчи при решении знаменитой «задачи о размножении кроликов».
(0),1, 1,
2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233....каждый член является суммой двух предыдущих
Представление чисел Фибоначчи в виде квадратов со стороной соответствующего размера
1170 – 1250 г.
Слайд 10
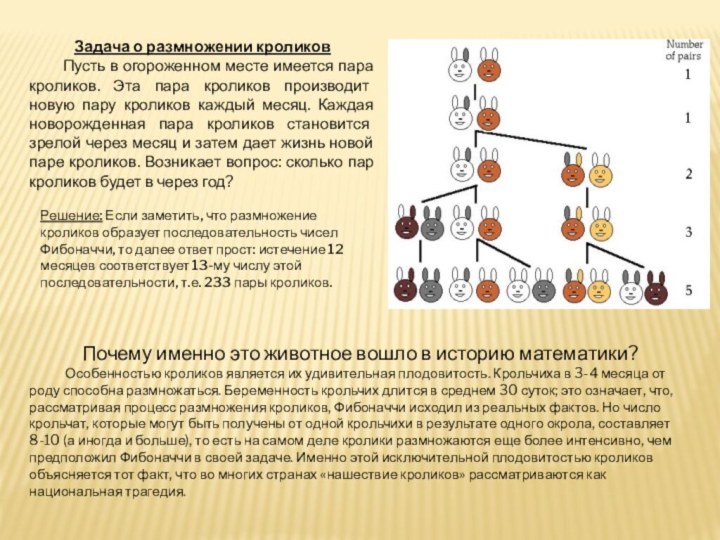
Почему именно это животное вошло в историю математики?
Особенностью
кроликов является их удивительная плодовитость. Крольчиха в 3-4 месяца
от роду способна размножаться. Беременность крольчих длится в среднем 30 суток; это означает, что, рассматривая процесс размножения кроликов, Фибоначчи исходил из реальных фактов. Но число крольчат, которые могут быть получены от одной крольчихи в результате одного окрола, составляет 8-10 (а иногда и больше), то есть на самом деле кролики размножаются еще более интенсивно, чем предположил Фибоначчи в своей задаче. Именно этой исключительной плодовитостью кроликов объясняется тот факт, что во многих странах «нашествие кроликов» рассматриваются как национальная трагедия.Задача о размножении кроликов
Пусть в огороженном месте имеется пара кроликов. Эта пара кроликов производит новую пару кроликов каждый месяц. Каждая новорожденная пара кроликов становится зрелой через месяц и затем дает жизнь новой паре кроликов. Возникает вопрос: сколько пар кроликов будет в через год?
Решение: Если заметить, что размножение кроликов образует последовательность чисел Фибоначчи, то далее ответ прост: истечение 12 месяцев соответствует 13-му числу этой последовательности, т.е. 233 пары кроликов.
Слайд 11
Легенда о создателе шахмат
Всего зерен 18 446 744 073
709 551 615!!!
ЧТО ПРЕДСТАВЛЯЕТ СОБОЙ ЭТО ЧИСЛО ГИГАНТ?!
В единицах массы: одно зёрнышко пшеницы имеет массу примерно 0,065 грамма, тогда общая масса пшеницы на шахматной доске составит около 1,200 триллионов тонн: 18 446 744 073 709 551 615 · 0,065 гр. = =1 199 038 364 791 120 854, 975 гр. =1 199 038 364 791, 120 т.
Это количество зерна превышает весь урожай пшеницы, собранный за всю историю человечества!!!
Если массу пшеницы перевести в объем (1 м3 пшеницы весит около 760 кг), то получится приблизительно 1500 км3, что больше всего объёма горы Эверест.
1+2+4+8+16+32+64+128+256+512+1024+2048+4096+8192…=?
увеличивая в 2 раза
Слайд 13
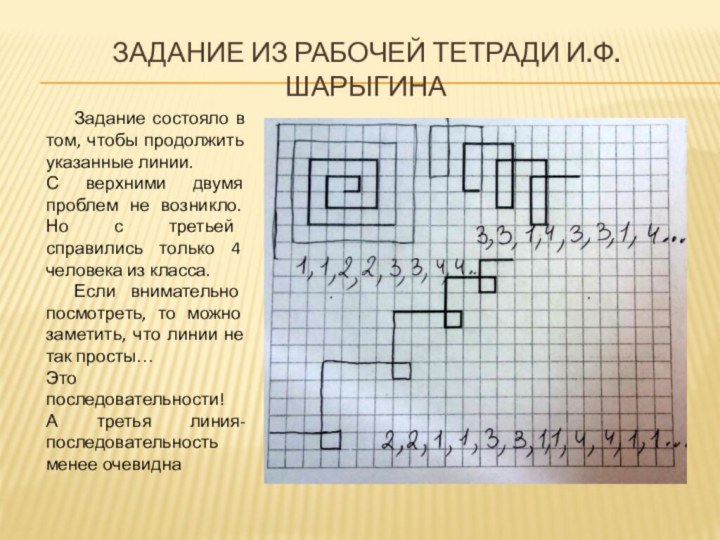
задание из рабочей тетради и.ф. Шарыгина
Задание состояло в
том, чтобы продолжить указанные линии.
С верхними двумя проблем
не возникло. Но с третьей справились только 4 человека из класса. Если внимательно посмотреть, то можно заметить, что линии не так просты…
Это последовательности!
А третья линия-последовательность менее очевидна
Слайд 18 Даны две последовательности: 2,4,8,16,14,10,2,4,… и 3,6,12,6,12,… В них
каждое число получено из предыдущего по одному и тому
же закону. Определите закономерность. Постройте по этому же закону последовательность в которой все члены равны между собой.Натуральные числа, делящиеся на 9, записаны в порядке возрастания: 9, 18, 27, 36,… Под каждым членом этой последовательности записана сумма его цифр. На каком месте во второй последовательности впервые появится число 81? Что во второй последовательности встретится раньше: первый раз число 36 или десять раз подряд число 27?
Восстанови последовательность чисел 7,_, _, _, _, _, _,9, если известно, что сумма любых трех чисел, стоящих подряд, равна 20.
Петя, Вася и Коля записали в ряд по 100 чисел.
У Пети пятое число равно 12, и каждое число начиная со второго на два больше левого соседа.
У Васи первое и третье число равны 4 и 6 соответственно, а каждое число, кроме крайних, вдвое меньше суммы его соседей.
А Коля просто записывал периметры прямоугольников шириной в одну клетку: сначала-периметр прямоугольника длиной в одну клетку, потом – длиной в две клетки, и так далее (сторона каждой клетки равна 1).
У кого из мальчиков совпали записанные ряды чисел?
Слайд 19
Посчитать сумму чисел 1+2+3+…+99+100
Выдающегося немецкого математика Карла Фридриха Гаусса (1777-1855) современники называли «королём математики».
Рассказывают, что в начальной школе, учитель, чтобы занять класс на продолжительное время самостоятельной работой, дал задание ученикам – вычислить сумму всех натуральных чисел от 1 до 100. Маленький Гаусс ответил на вопрос почти мгновенно, чем невероятно удивил всех и, прежде всего, учителя.
Как ему это удалось?
Что заметил юный Гаусс?
Подумайте в каких последовательностях можно пользоваться приемом юного Гаусса при вычислении суммы членов последовательности?
Слайд 20 При хранении бревен их укладывают, как показано на
рисунке. Сколько бревен находится в одной кладке, если в
ее основании положено 12 бревен.2. В благоприятных условиях бактерии размножаются так, что на протяжении одной минуты одна из них делится на две. Найдите количество бактерий, рожденных одной бактерией за 7 мин.
Вопросы к задачам:
Составьте последовательности к задачам. В какой задаче закон, по которому образована последовательность, отличается от остальных?
Решите задачи, пользуйтесь при необходимости идеями юного Гаусса.
Кто быстрее размножаются кролики (задача рассматривалась выше) или бактерии?
Кто накопит большую сумму за 7 месяцев? Родители Андрея из задачи 4. или Максима, если они откладывают каждый месяц сумму вдвое большую, чем в предыдущем месяце, начиная с 50 рублей? А за 3 месяца? За 12 месяцев?
3. Петр решил заняться бегом, начав с 200 м и увеличивая дистанцию ежедневно на 50 м. Через сколько дней Петр сможет пробежать 2 км?
4. Родители ко Дню рождения своего сына решили купить ему мобильный телефон. Для этого они в первый месяц отложили 650 рублей, а каждый следующий месяц они откладывали на 50 рублей больше, чем в предыдущий. Какая сумма будет у родителей Андрея через 7 месяцев.
Слайд 22
- это способ запоминания цифровой информации поиском закономерностей.
Если внимательно рассмотреть число, то можно обнаружить различные последовательности
цифр: Например: 674523. В этой последовательности можно увидеть четную последовательность 6-4-2 и нечетную последовательность 7-5-3.Или можно обнаружить другие закономерности, например, симметрию 738837, 2630362.
Метод “Математических последовательностей”-
Мы нашли закономерности в числах дат рождения наших близких…Теперь не забудем!