Слайд 2
Содержание
1.Введение.
Цель исследования……………………………….…………..2
Задачи исследования….………………………..…………….2
Актуальность………………………………...………………..2
2. Основная часть…………………………………………….2
2.1 История исследования музыки
и математики………….2
2.2 Связь математики и музыки……………………………...5
2.3 Связь цифр и
музыки……………………………………..6
3.Заключение…………………………………………7
4. Список используемой литературы………………10
5. Приложение
Слайд 3
Музыка и математика
«Музыка есть таинственная
арифметика души;
Она вычисляет, сама того не
подозревая».
Г. Лейбниц.
Наверняка, каждый из вас сейчас подумал, какая же связь может быть между математикой – мудрой царицей всех наук, и музыкой?
И сегодня в нашей работе, мы предлагаем вам найти ответы на эти вопросы.
Слайд 4
Музыка и математика
Цель:
Доказать, что связь между музыкой
и математикой существует.
Задачи:
Проанализировать литературу по теме исследования;
Сравнить материал, изучаемый на уроке музыки, на кружке по музыке и материал, который изучают ученики в школьном курсе математики;
Определить взаимосвязь музыки и математики;
Способствовать формированию нового взгляда на мир;
Формировать потребность поиска ответов на возникающие вопросы;
Развивать творческие способности учащихся, ассоциативное мышление, воображение и фантазию;
Воспитывать открытую, свободную личность, способную к познанию, активному действию.
Слайд 5
Математика и музыка
Актуальность:
Музыка помогает изучать
математику.
Музыкальные и математические операции родственны и
содержательно, и психологически.
Занимаясь музыкой, человек развивает и тренирует математические способности
Слайд 6
Методы исследования
Изучение, обработка и анализ документов
Метод исследования музыкального
произведения
Слайд 7
Цифровые обозначения
Как
и в математике, в музыке встречаются
цифры: звукоряд
– 7 нот,
нотный стан – 5 линеек,
интервалы: прима – 1,
секунда – 2,
терция – 3,
кварта – 4,
квинта – 5,
секста – 6,
септима – 7,
октава – 8.
Слайд 8
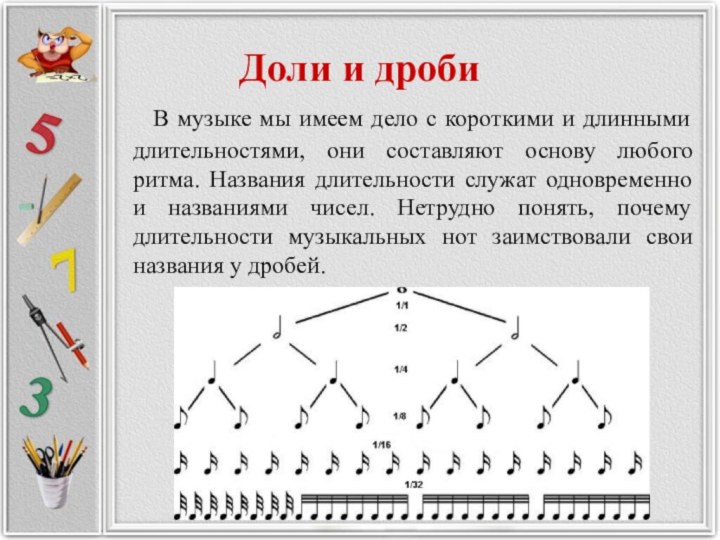
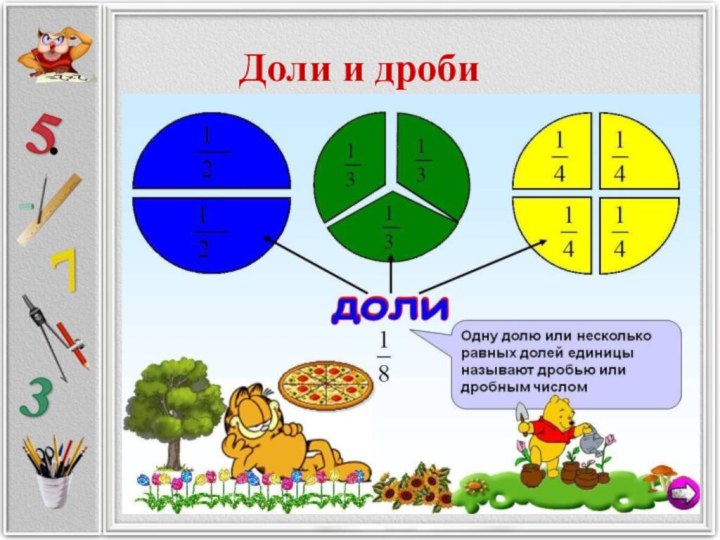
Доли и дроби
В музыке мы имеем
дело с короткими и длинными длительностями, они составляют основу
любого ритма. Названия длительности служат одновременно и названиями чисел. Нетрудно понять, почему длительности музыкальных нот заимствовали свои названия у дробей.
Слайд 10
Доли и дроби
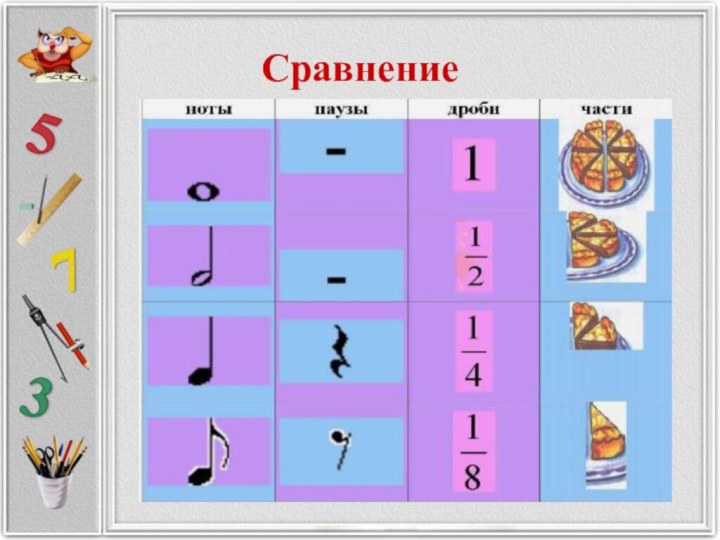
Длительности получаются
так же,
как дроби:
они возникают при делении
целой
ноты на равные доли.
Поэтому длительность
можно подсчитывать как
дробные числа,
например:
Слайд 12
Математические последовательности
Из нашей тетради по математике для 4
класса:
Разгадай закономерность, по которой записан каждый ряд чисел, и
продолжи его ещё тремя числами:
1)108; 324; 972; 2916;………………….
2)645; 769; 885; 1005;………………….
3)1024; 1004; 984; 964;………………...
Слайд 13
Музыкальные последовательности
Все музыкальные произведения
записываются нотами в музыкальной последовательности
Слайд 14
Противоположности в математике
Отрицательное число – положительное число,
Плюс –
минус,
Деление – умножение,
Четное число – нечетное число,
Больше – меньше,
Простое
число – составное число и т.д.
Слайд 15
Противоположности
в музыке
Медленно – быстро,
Высоко – низко,
Громко –
тихо,
Быстро – медленно,
Длинный – короткий,
Многоголосие – соло,
Вокальное исполнение –
инструментальное исполнение,
Диез – бемоль и т. д.
Слайд 16
Учение Пифагора
Пифагор создал целое учение о гармонии
и главную роль в этом учении отводил числам. Особое
значение придавал он первым четырём числам натурального ряда – 1, 2, 3 и 4. По его мнению, эти числа лежат в основе всякой гармонии. Пифагор считал эти числа фундаментом мировой гармонии. Он пристально изучал
их соотношения, и очень
неожиданно применил их в
музыке.
Слайд 17
Учение Пифагора
Пифагор взял обыкновенную струну и натянул её
на доску. Если прижать струну к грифу, то звук,
издаваемый ей, получится гораздо тоньше первого, или как говорят музыканты, выше.
Разность этих высот (интервал) между ними, принято называть октавой.
Слайд 18
Связь между числами и музыкой.
I группа (дети, у которых
аккорды благозвучные):
Гачегов Даниил (31.05.2004) - занимается танцами, любит петь
Сотникова
Валерия (14.03.2005) - пишет стихи, любит рисовать
Коев Максим (08.04.2004) – любит рисовать и петь
Грызунова Валентина (15.05.2004) – любит петь, рисовать, занимается в театральном кружке
Мишенин Александр (06.04.2004) – любит петь, танцевать, играет на аккордеоне
Слайд 19
Связь между числами и музыкой.
II группа (дети, у которых
аккорды не благозвучные):
1. Лукина Арина (23.03.2003)– любит играть в
настольные и компьютерные игры
2. Комогорцева Анастасия (28.11.2003) – любит решать задачи, головоломки
3. Котенев Артемий (08.04.2003)– играет в футбол
4. Ковальчук Даниил (09.12.2003) – занимается горнолыжным спортом
5. Вишневская Екатерина (30.06.2003) – любит решать задачи, занимается спортом.
Слайд 20
ЗАКЛЮЧЕНИЕ
Выводы:
В математике и музыке можно наблюдать такие
схожие понятия, как ритм, последовательности, доли и дроби, противоположности,
цифровые обозначения
Эти понятия используются во всех предметах, но не всегда выражают одно и то же.
Математический язык так же, как и любой язык или музыка, обладают определенной структурой.