Слайд 2
Вводная часть
Интерактивная презентация предназначена для закрепления материала учебной
дисциплины «Геометрия» для обучающихся 1 курса (10 класс).
Наименование темы
в Рабочей программе учебной дисциплины «Прямые и плоскости в пространстве».
Для обучающихся
При изучени учебного материала на слайдах записывайте в конспекте ответы на вопросы в порядке их следования.
Презентация построена таким образом, что Вы можете, после своих ответов в конспекте, увидеть правильные ответы на слайде и проверить свои знания по данной теме. Это касается как текстовых вопросов, так и вычислительных задач. Задачи требуют решения.
Презентация нацелена на повышение интереса к предмету, самоконтролю, самостоятельному обучению обучающихся, а также оценивание и закрепление своих знаний в режиме реального времени.
Удачи!
Слайд 3
Базовые объекты геометрии
Точка
Прямая
Луч
Отрезок
Ломаная
Слайд 4
Практическое применение геометрии бесценно во все времена и
независимо от профессии. Без знаний геометрии не может обойтись
ни рабочий, ни инженер, ни архитектор и даже художник.
В геометрии есть такой раздел, который занимается изучением различных фигур на плоскости и называется планиметрия.
Слайд 5
«Геометрия» - составлено из двух греческих слов:
«geо» и «metreo». «Гео» - по-гречески земля, а «метрио»
- мерить. В переводе с греческого слово «геометрия» означает «землемерие», так как в стародавние времена основной задачей геометрии, как науки, стало измерение расстояний и площадей на поверхности земли.
Геометрия — это раздел математики, изучающий геометрические фигуры и их свойства.
Задание 1. Закончить смысловую часть определения
Слайд 6
Что такое геометрическая фигура?
Геометрические фигуры – это совокупность
множества точек, линий, поверхностей или тел, которые расположены на
поверхности, плоскости или пространстве и формирует конечное количество линий.
Термин «фигура» в какой-то степени формально применяется к множеству точек, но как правило фигурой принято называть такие множества, которые расположенные на плоскости и ограничиваются конечным числом линий.
Геометрическая фигура (тело) – абстрактный предмет, в котором рассматривается только форма и размер, не обращая внимания на физические свойства.
Итак,
Фигурой называют произвольное множество точек, находящиеся на плоскости.
Слайд 7
К основным понятиям геометрии относятся:
точка,
прямая,
плоскость.
Они даются
без определения, но определения других геометрических фигур даются через
эти понятия.
Задание 2. Назовите термины
Слайд 8
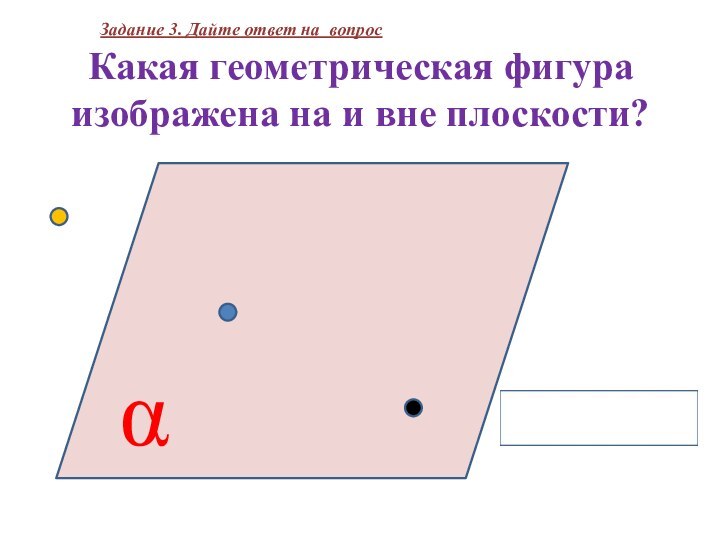
α
Какая геометрическая фигура изображена на и вне плоскости?
Задание
3. Дайте ответ на вопрос
Точка
Слайд 9
Точка — это основная и самая простая геометрическая
фигура.
Точка
Точка является идеализацией объектов, размерами которых можно пренебречь.
Древнегреческий учёный
Евклид (около 300 г. до н. э.) определял точку как то, что не имеет частей.
Слайд 10
Точки изображают карандашом или ручкой на листе бумаги,
мелом на доске, соответствующими инструментами в компьютерных
графических редакторах и
т. п.
Однако точка, нарисованная карандашом, всегда имеет хоть и маленькие, но ненулевые размеры, а
геометрическая точка размеров не имеет.
Для обозначения точек используются прописные латинские буквы, например A, B, C, ..., A1, B2, C3, …
Слайд 11
В геометрии точка обозначается заглавной латинской буквой, например
A, B, C, ..., A1, B2, C3, или цифрой.
Многие латинские буквы по написанию похожи на английские буквы.
В тексте точку обозначают следующим символом: (·) A — точка А
Слово «точка» в переводе с латинского языка означает результат мгновенного касания, укол.
Точка является основой для построения любой геометрической фигуры.
Слайд 12
Задание 4. Дайте ответ на вопрос
Слайд 13
Точка — это самая малая геометрическая фигура, которая является основой
всех прочих построений (фигур) в любом изображении или чертеже.
Задание
5. Закончить смысловую часть определений
Слайд 14
Задание 6. Дайте ответ на вопрос
Всякая более
сложная геометрическая фигура — это множество точек, которые обладают определенным
свойством, характерным только для этой фигуры.
Слайд 15
Набор точек на плоскости
В геометрии, топологии и близких разделах
математики то́чкой называют абстрактный объект в
пространстве, не имеющий ни объёма, ни площади,
ни длины, ни каких-либо других измеримых характеристик.
Точка является одним из фундаментальных
понятий в математике; любая геометрическая фигура считается состоящей из точек.
Всё о точке!
Слайд 16
Аксиома 1.
Через любые две точки пространства проходит
единственная
прямая.
Задание 7. Закончить смысловую часть определения
Аксиомы стереометрии
Слайд 17
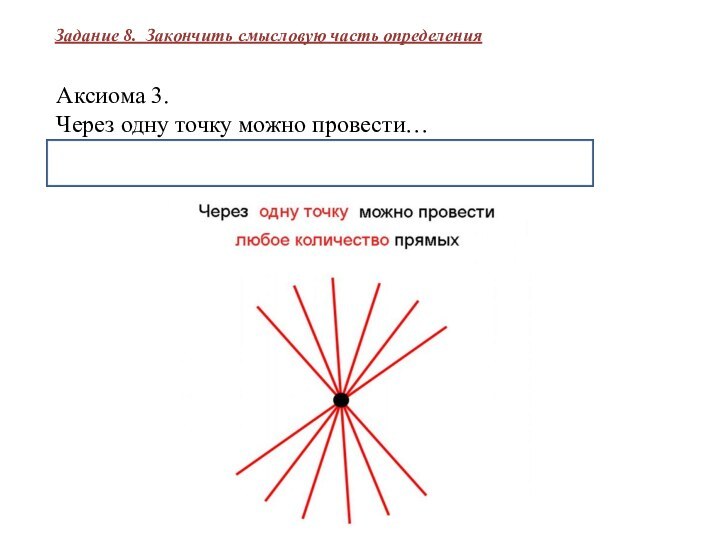
Аксиома 3.
Через одну точку можно провести… бесконечное множество
прямых.
Задание 8. Закончить смысловую часть определения
Слайд 18
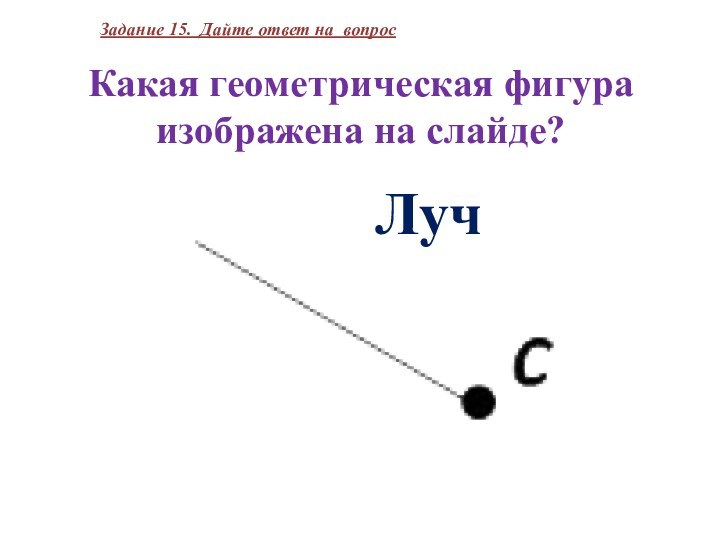
Какая геометрическая фигура изображена на слайде?
Задание 9. Дайте
ответ на вопрос
Прямая
Слайд 19
Прямая
Прямая — это самая простая геометрическая фигура, которая
не имеет ни начала, ни конца.
Слайд 20
Слова «не имеет ни начала, ни конца» говорят
о том, что прямая бесконечна.
Две прямые могут пересекаться только
в… одной точке.
Задание 10. Закончить смысловую часть определения
Прямая является идеализацией натянутой нити, края стола
прямоугольной формы и т. п.
Евклид определял прямую как длину без ширины.
Прямые проводят карандашом или ручкой на листе бумаги или
доске с помощью линейки, соответствующими инструментами в
компьютерных графических редакторах.
Слайд 21
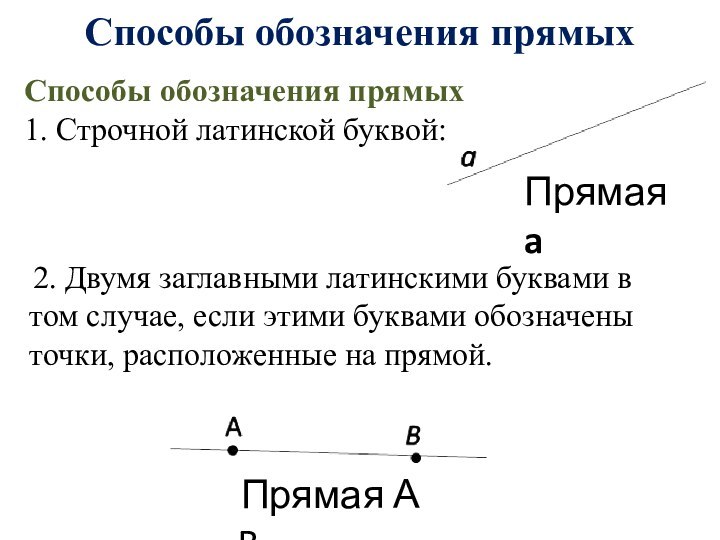
Способы обозначения прямых
1. Строчной латинской буквой:
Способы обозначения прямых
Прямая a
2.
Двумя заглавными латинскими буквами в том случае, если этими
буквами обозначены точки, расположенные на прямой.
Прямая АB.
Слайд 22
Прямую линию, или прямую, можно представить себе как
бесчисленное множество точек, которые расположены на одной линии, не
имеющей ни начала, ни конца. На листе бумаги мы видим только часть прямой линии, так как она бесконечна.
Можно утверждать, что прямая линия бесконечна и не имеет предела.
Без начала и без края
Линия прямая.
Хоть сто лет по ней идти,
Не найдешь конца пути.
Слайд 23
Расположение прямых линий может быть таким, как изображено
на примерах ниже.
Прямая линия или просто прямая
– это линия, вдоль которой расстояние между двумя точками является кратчайшим. Прямая линия бесконечна, и изобразить всю прямую и измерить её невозможно.
Задание 11. Укажите типы линий
Слайд 24
Теорема. Если прямая имеет с плоскостью две общие
точки, то она лежит в этой плоскости.
Если точка принадлежит
прямой, то говорят, что прямая проходит через эту точку.
Если точка не принадлежит прямой, то говорят также, что прямая не проходит через эту точку.
Задание 12. Закончить смысловую часть определения
Слайд 25
Задача 1.
На одной прямой на равном расстоянии
друг от друга стоят три телеграфных столба. Крайние находятся
от дороги на расстояниях 18 м и 48 м.
Найдите расстояние, на котором находится от дороги средний столб.
Задание 13. Найдите решение задачи
Ответ: 33
Запишите ответ в листе подсчёта баллов.
Подумали?
Решили?
Слайд 26
Задание 14. Найдите решение задачи
Задача 2.
Мальчик прошел
от дома по направлению на восток 800 м. Затем
повернул на север и прошел 600 м. На каком расстоянии от дома оказался мальчик?
Запишите ответ в листе подсчёта баллов.
Ответ: 1000
Слайд 27
Какая геометрическая фигура изображена на слайде?
Задание 15. Дайте
ответ на вопрос
Луч
Слайд 28
Луч
Луч — это часть прямой линии, которая расположена
по одну сторону от какой-либо… точки.
У луча есть начало,
но нет конца.
Луч — это направленная полупрямая, которая имеет точку начала и не имеет конца.
Задание 16. Закончить смысловую часть определения
Задание 17. Закончить смысловую часть определения
Слайд 29
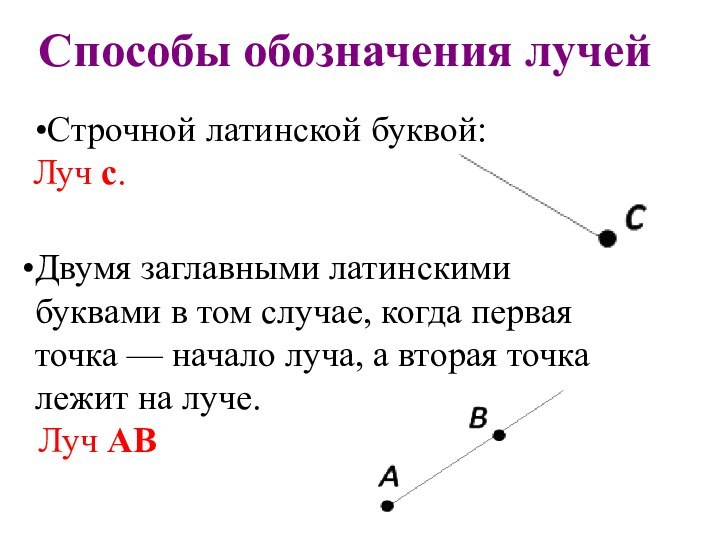
Строчной латинской буквой:
Луч c.
Способы обозначения лучей
Двумя заглавными латинскими
буквами в том случае, когда первая точка — начало
луча, а вторая точка лежит на луче.
Луч AB
Слайд 30
Если на прямой вы поставили точку, то этой точкой прямая разбивается
на два луча, противоположно направленных.
Такие лучи называются дополнительными.
Задание 18. Закончить смысловую
часть определения
Слайд 31
Какая геометрическая фигура изображена на слайде?
Задание 19. Дайте
ответ на вопрос
Отрезок
Слайд 32
Отрезок
У отрезка есть и начало, и конец.
Отрезок — это часть
прямой линии, которая ограничена двумя точками (концами отрезка).
Задание 20.
Закончить смысловую часть определения
Слайд 33
Основное свойство отрезка — это его длина.
Длина отрезка
— это расстояние между его концами.
В математике отрезок обозначается
заглавными латинскими буквами.
Свойства отрезка
Отрезок AB.
Можно сказать, что точки АВ лежат на прямой а или принадлежат прямой а. А можно сказать, что прямая а проходит через точки А и В.
Задание 21. Закончить смысловую часть определения
Слайд 34
Задача 3.
На вершинах двух елок сидят две
вороны. Высота елок равна 4 м и 6 м.
Расстояние между ними равно 10 м. На каком расстоянии BE нужно положить сыр для этих ворон, чтобы они находились в равных условиях, т.е. чтобы расстояния от них до сыра было одинаковыми?
Задание 22. Найдите решение задачи
Ответ: 6 метров
Слайд 35
?
?
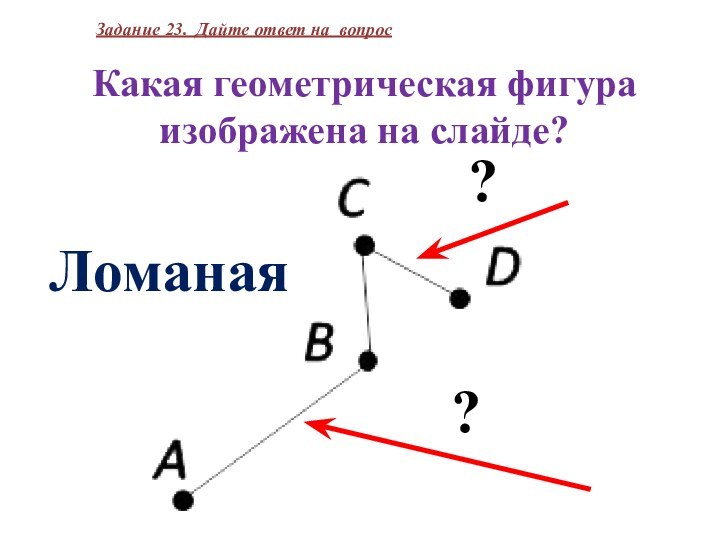
Какая геометрическая фигура изображена на слайде?
Задание 23. Дайте
ответ на вопрос
Ломаная
Слайд 36
Ломаная
Ломаная — это геометрическая фигура, состоящая из точек,
которые соединены отрезками.
ИЛИ
Если же перед вами несколько отрезков,
соединенных между собой так, что конец первого отрезка становиться началом второго, а конец второго отрезка — началом третьего и т. д., и эти отрезки находятся не на одной прямой и при соединении имеют общую точку, то такая цепочка является ломаной линией.
Слайд 37
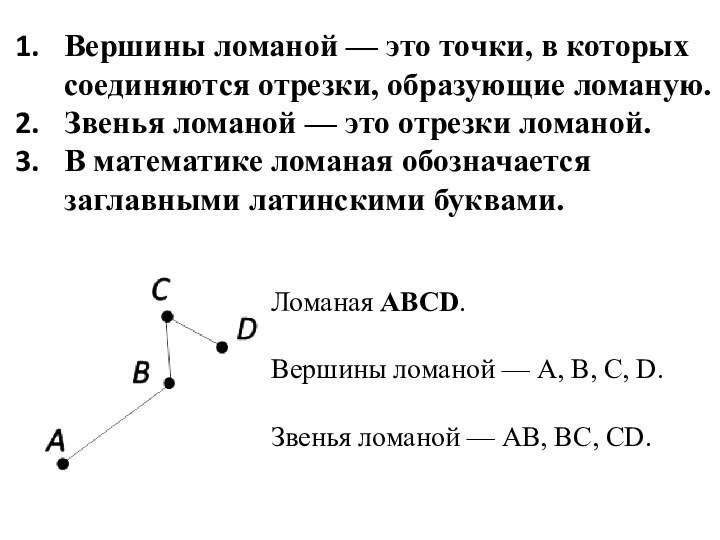
Вершины ломаной — это точки, в которых соединяются
отрезки, образующие ломаную.
Звенья ломаной — это отрезки ломаной.
В математике
ломаная обозначается заглавными латинскими буквами.
Ломаная ABCD.
Вершины ломаной — A, B, C, D.
Звенья ломаной — AB, BC, CD.
Слайд 38
Чтобы найти длину ломаной, необходимо сложить длины всех
её звеньев (отрезков), из которых она состоит.
KLCM = KL +
LC + CM = 3 см + 2 см + 2 см = 7 см.
Слайд 39
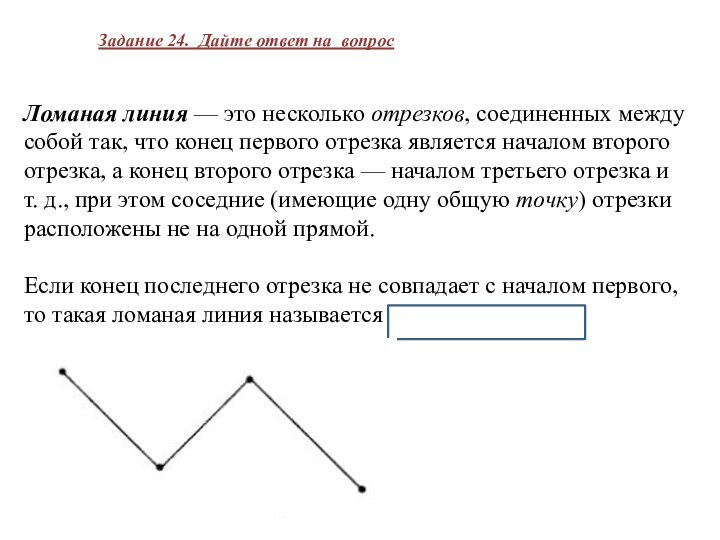
Ломаная линия — это несколько отрезков, соединенных между собой так,
что конец первого отрезка является началом второго отрезка, а
конец второго отрезка — началом третьего отрезка и т. д., при этом соседние (имеющие одну общую точку) отрезки расположены не на одной прямой.
Если конец последнего отрезка не совпадает с началом первого, то такая ломаная линия называется незамкнутой.
Задание 24. Дайте ответ на вопрос
Слайд 40
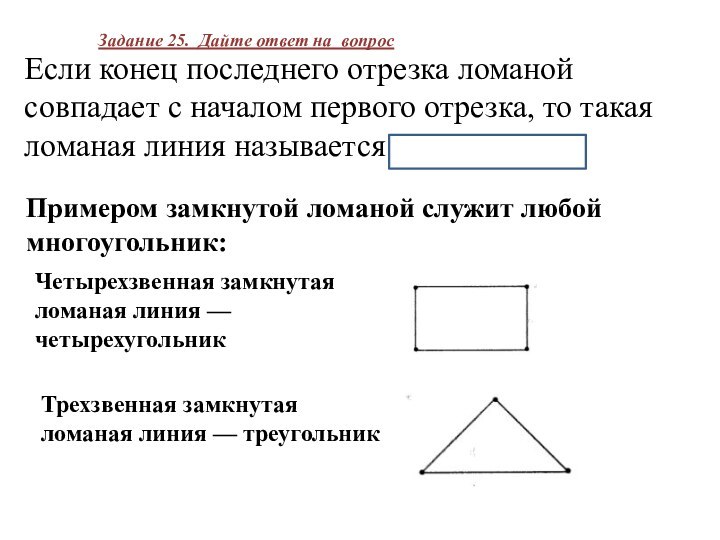
Если конец последнего отрезка ломаной совпадает с началом
первого отрезка, то такая ломаная линия называется замкнутой.
Задание 25.
Дайте ответ на вопрос
Примером замкнутой ломаной служит любой многоугольник:
Четырехзвенная замкнутая ломаная линия — четырехугольник
Трехзвенная замкнутая ломаная линия — треугольник
Слайд 41
Задание 26. Дайте ответ на вопрос
Слайд 42
Задание 27. Дайте ответ на вопрос
Слайд 43
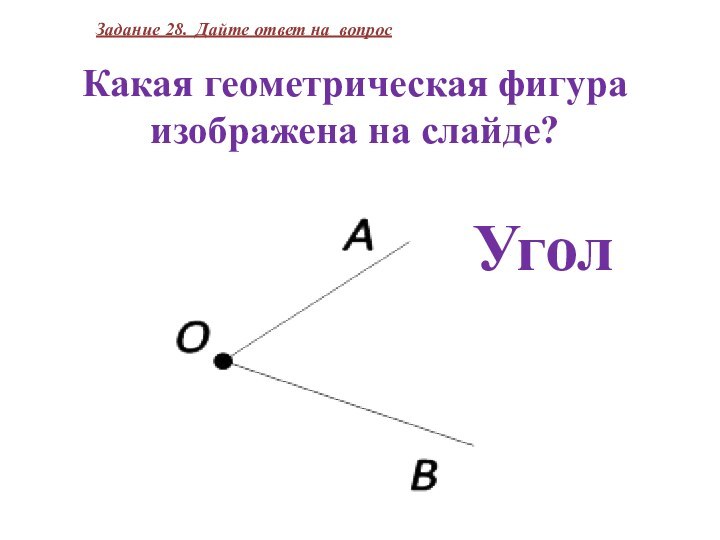
Какая геометрическая фигура изображена на слайде?
Задание 28. Дайте
ответ на вопрос
Угол
Слайд 44
Угол — это геометрическая фигура, которая состоит из
двух лучей и вершины.
Вершина угла — это точка, в
которой два луча берут начало.
Стороны угла — это лучи, которые образуют угол.
Вершина угла — точка O.
Стороны угла — OA и OB.
Задание 29. Закончить смысловую часть определения
Слайд 45
1. Одной заглавной латинской буквой, указывающей его вершину.
Способы
обозначения углов
2. Тремя заглавными латинскими буквами, которыми обозначены вершина
и две точки, расположенные на сторонах угла.
Слайд 46
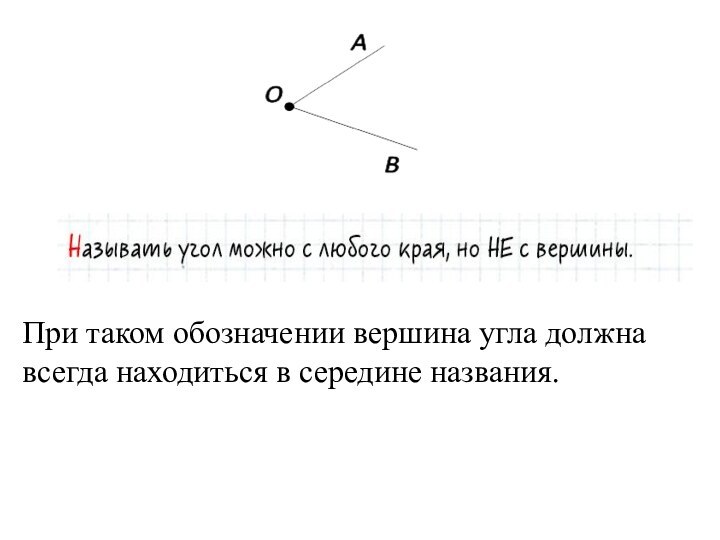
При таком обозначении вершина угла должна всегда находиться
в середине названия.
Слайд 47
Единица измерения углов — градусы. Углы измеряют с
помощью специального прибора — транспортира.
Для обозначения градусов в тексте
используется символ: °
50 градусов обозначаются так: 50°
Задание 30. Дайте ответ на вопрос
Слайд 48
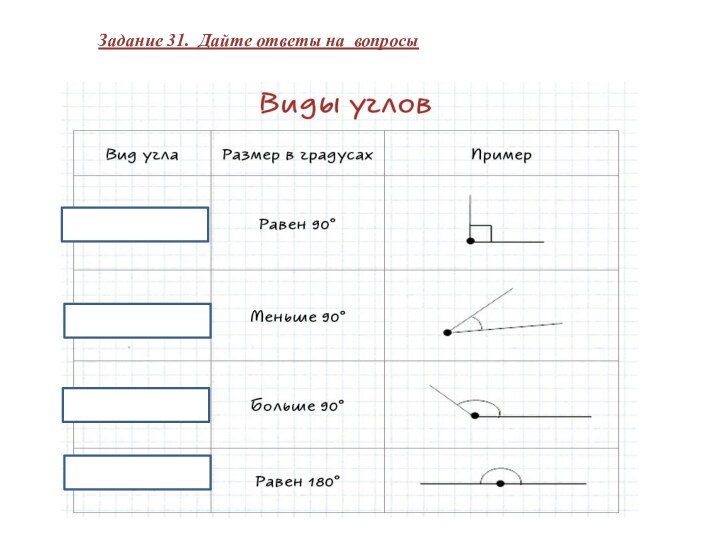
Задание 31. Дайте ответы на вопросы
Слайд 49
Задание 32. Дайте ответ на вопрос
Слайд 50
Два угла могут иметь одну общую сторону.
Обратите внимание
на рисунок ниже. Попробуйте сосчитать и назвать все углы
на изображении.
Задание 33. Дайте ответы на вопросы
Слайд 51
Задание 34. Дайте ответ на вопрос
Слайд 52
Задание 35. Дайте ответ на вопрос
Слайд 53
Плоскость, как и прямая, — это первичное понятие,
не имеющее определения.
У плоскости, как и у прямой,
нельзя видеть ни начала, ни конца.
Мы рассматриваем только часть плоскости, которая ограничена замкнутой ломаной линией.
Примером плоскости является поверхность вашего рабочего стола, тетрадный лист, любая гладкая поверхность. Плоскость можно изобразить как заштрихованную
геометрическую фигуру:
Поверхности стола, школьной доски, оконного стекла дают представление о плоскости.
Эти поверхности имеют края.
У плоскости края нет. Она безгранично простирается во всех направлениях.
Слайд 54
Аксиома.
Через любые три точки пространства, не принадлежащие
одной прямой, проходит единственная плоскость.
Аксиома. Если две плоскости имеют
общую точку, то они пересекаются по прямой.
Теорема . Через прямую и не принадлежащую ей точку проходит единственная плоскость.
Задание 36. Закончить смысловую часть определения
Слайд 55
Плоскость идеализирует поверхность пола, стены, стола,
зеркала и
т. п.
Если точка принадлежит плоскости, то говорят, что плоскость
проходит
через эту точку.
Если точка не принадлежит плоскости, то говорят также, что
плоскость не проходит через эту точку.
Для обозначения плоскостей используются строчные греческие
буквы α, β, γ, ... или тройки прописных латинских букв АВС,
DEF, A1B1C1 и т. д., указывающих какие-нибудь три точки, принадлежащие этой плоскости и не принадлежащие одной прямой.
Слайд 56
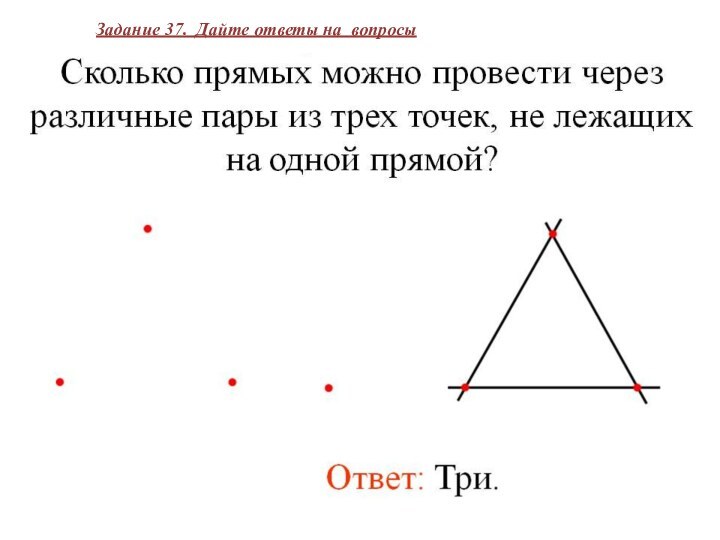
Задание 37. Дайте ответы на вопросы
Слайд 57
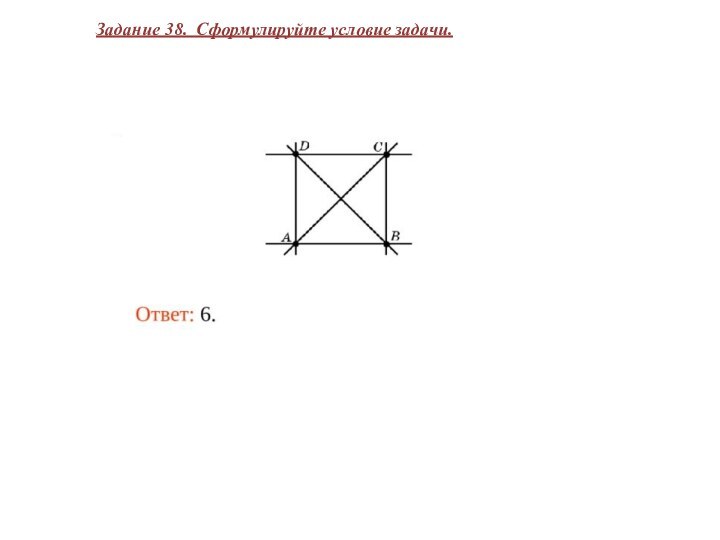
Задание 38. Сформулируйте условие задачи.
Слайд 58
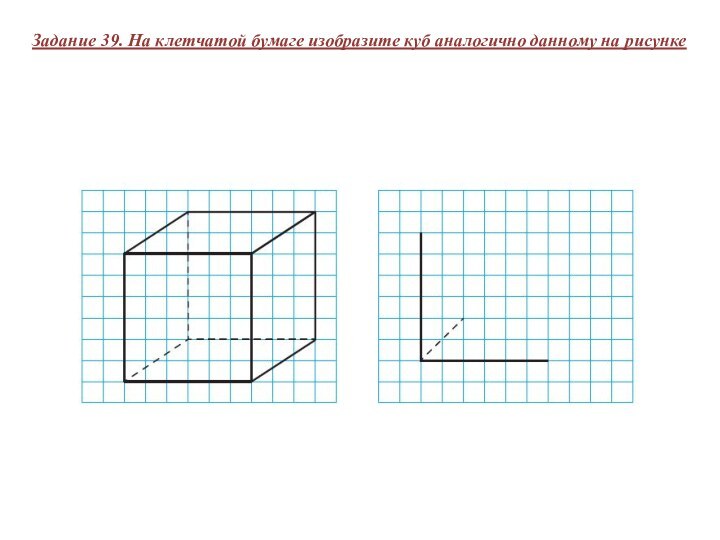
Задание 39. На клетчатой бумаге изобразите куб аналогично
данному на рисунке
Слайд 59
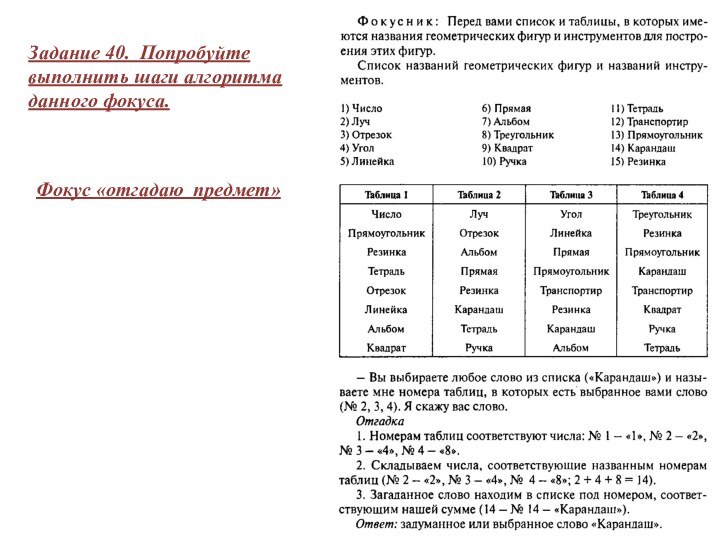
Фокус «отгадаю предмет»
Задание 40. Попробуйте выполнить шаги алгоритма
данного фокуса.
Слайд 60
Предоставьте отчёт о выполненных заданиях.
Там, где ответ текстовый
- текст,
там где вычисления – образец решения,
там где чертеж
– рисунок и т.д.