Слайд 2
Введение: Понятие «Треугольник»
Фигура «Треугольник» в геометрии является
одной из самых простых и важных фигур. В большинстве
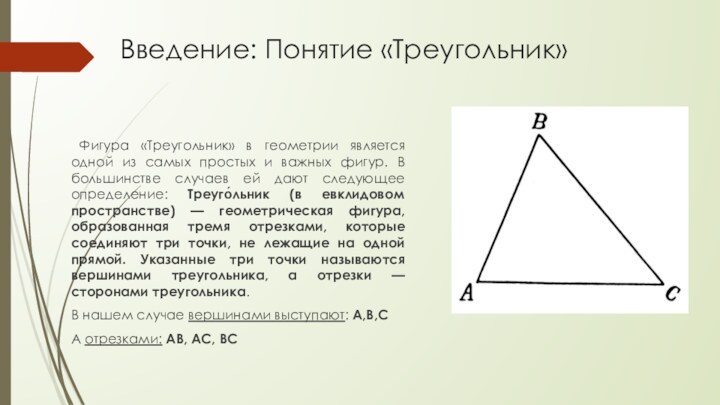
случаев ей дают следующее определение: Треуго́льник (в евклидовом пространстве) — геометрическая фигура, образованная тремя отрезками, которые соединяют три точки, не лежащие на одной прямой. Указанные три точки называются вершинами треугольника, а отрезки — сторонами треугольника.
В нашем случае вершинами выступают: А,В,С
А отрезками: АВ, АС, ВС
Слайд 3
Напомним что две фигуры, в частности два треугольника,
называются равными если их можно совместить, наложив друг на
друга. В данном случае на картинке мы видим два равных треугольника АВС и А1В1С1
Таким образом, если треугольники равны, то их элементы (т.е. углы и стороны) одного треугольника соответственно равны углам и сторонам другого треугольника.
Введение: Понятие «равенства треугольников»
Слайд 4
Первый признак равенства треугольников
Теорема:(Первый признак равенства треугольников —
по двум сторонам и углу между ними) Если две
стороны и угол между ними одного треугольника соответственно равны двум сторонам и углу между ними другого треугольника, то такие треугольники равны.
Слайд 5
Первый признак равенства треугольников(доказательство)
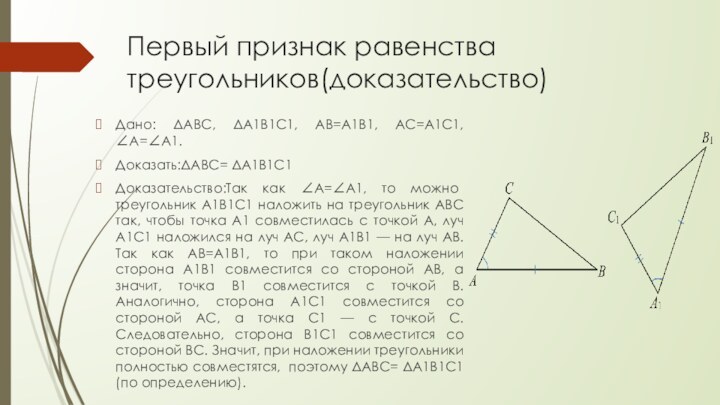
Дано: ΔABC, ΔA1B1C1, AB=A1B1, AC=A1C1,
∠A=∠A1.
Доказать:ΔABC= ΔA1B1C1
Доказательство:Так как ∠A=∠A1, то можно треугольник A1B1C1 наложить
на треугольник ABC так, чтобы точка A1 совместилась с точкой A, луч A1C1 наложился на луч AC, луч A1B1 — на луч AB. Так как AB=A1B1, то при таком наложении сторона A1B1 совместится со стороной AB, а значит, точка B1 совместится с точкой B. Аналогично, сторона A1C1 совместится со стороной AC, а точка C1 — с точкой C. Следовательно, сторона B1C1 совместится со стороной BC. Значит, при наложении треугольники полностью совместятся, поэтому ΔABC= ΔA1B1C1 (по определению).
Слайд 6
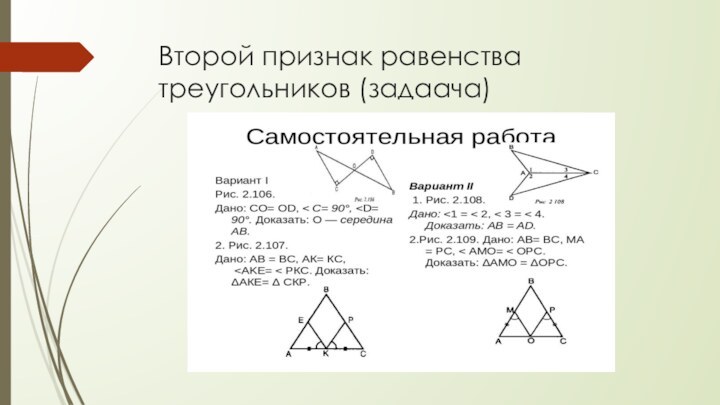
Первый признак равенства треугольников (Задача)
Слайд 7
Второй признак равенства треугольников
Теорема (Второй признак равенства
треугольников — по стороне и двум прилежащим к ней
углам)
Если сторона и прилежащие к ней углы одного треугольника соответственно равны стороне и прилежащим к ней углам другого треугольника то такие треугольники равны.
Слайд 8
Второй признак равенства треугольников (доказательство)
Дано: ΔABC, ΔA1B1C1,AB=A1B1, ∠A=∠A1,
∠B=∠B1.
Доказать:ΔABC= ΔA1B1C1
Доказательство:
Так как AB=A1B1, то треугольник A1B1C1 можно наложить
на треугольник ABC так, чтобы:1)сторона A1B1 совместилась со стороной AB,2)точки C1 и С лежали по одну сторону от прямой AB.
Поскольку ∠A=∠A1, сторона A1С1 при этом наложится на луч AC.Так как ∠B=∠B1, сторона B1C1 наложится на сторону BC. Точка С1 принадлежит как стороне A1С1, так и стороне B1C1, поэтому С1 лежит и на луче AC, и на луче CB. Лучи AC и CB пересекаются в точке C. Следовательно, точка С1 совместится с точкой C. Значит, сторона A1С1 совместится со стороной AC, а сторона B1C1 — со стороной BC. Таким образом, при наложении треугольники ABC и A1B1C1 полностью совместятся. А это означает, что ΔABC= ΔA1B1C1 (по определению).
Слайд 9
Второй признак равенства треугольников (задаача)
Слайд 10
Третий признак равенства треугольников
Теорема(Третий признак равенства треугольников
— по трём сторонам)
Если три стороны одного треугольника соответственно
равны трём сторонам другого треугольника, то такие треугольники равны.
Слайд 11
Третий признак равенства треугольников (доказательство)
Дано:ΔABC,ΔA1B1C1,AB=A1B1, AC=A1C1, BC=B1C1.
Доказать:ΔABC= ΔA1B1C1
Доказательство:Приложим
треугольник A1B1C1 к треугольнику ABC так, чтобы:
вершина A1
совместилась с вершиной A,
вершина B1 совместилась с вершиной B,
точки C1 и C лежали по разные стороны от прямой AB.
При этом возможны три случая взаимного расположения луча CC1 и угла ACB.
Слайд 12
Третий признак равенства треугольников (доказательство)
I. Луч CC1 проходит
внутри угла ACB.
Проведём отрезок CC1.
По условию AC=A1C1 и BC=B1C1,
поэтому треугольники ACC1 и BCC1 — равнобедренные с основанием CC1.
По свойству равнобедренного треугольника, ∠ACC1=∠AC1C и ∠BCC1=∠BC1C.
Если к равным углам прибывать равные углы, то получим равные углы:
Таким образом, ∠ACB=∠AC1B.
Точки A1 и A, B1 и B совмещены, то есть ∠AC1B и ∠A1C1B1 — один и тот же угол.
Для треугольников ABC и A1B1C1 имеем: AC=A1C1, BC=B1C1 (по условию), ∠ACB=∠A1C1B1 (по доказанному).
Следовательно, ΔABC= ΔA1B1C1 (по 1 признаку равенства треугольников).
Слайд 13
Третий признак равенства треугольников (доказательство)
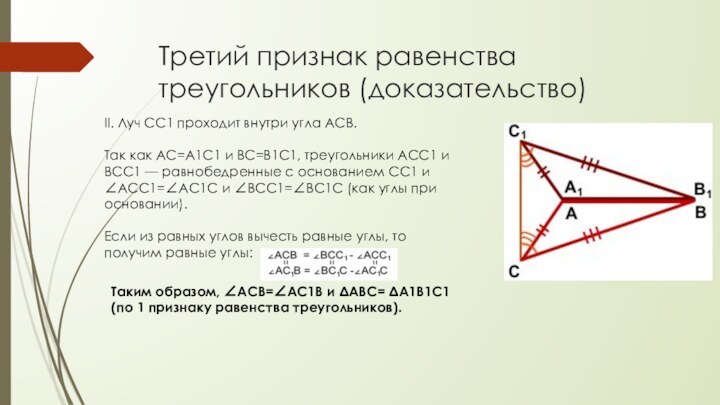
II. Луч CC1 проходит
внутри угла ACB.
Так как AC=A1C1 и BC=B1C1, треугольники ACC1
и BCC1 — равнобедренные с основанием CC1 и ∠ACC1=∠AC1C и ∠BCC1=∠BC1C (как углы при основании).
Если из равных углов вычесть равные углы, то получим равные углы:
Таким образом, ∠ACB=∠AC1B и ΔABC= ΔA1B1C1 (по 1 признаку равенства треугольников).
Слайд 14
Третий признак равенства треугольников (доказательство)
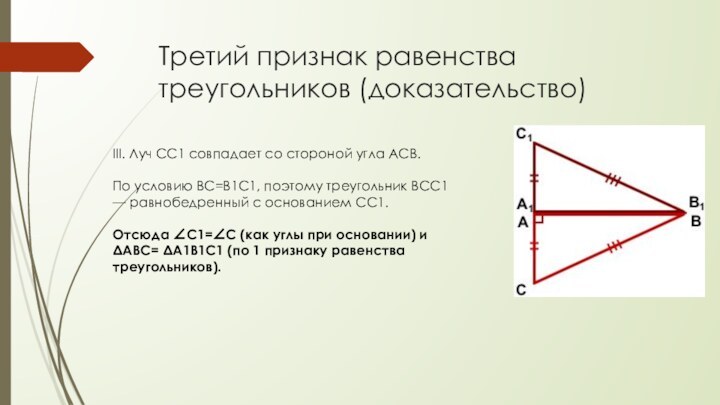
III. Луч CC1 совпадает
со стороной угла ACB.
По условию BC=B1C1, поэтому треугольник BCC1
— равнобедренный с основанием CC1.
Отсюда ∠C1=∠C (как углы при основании) и ΔABC= ΔA1B1C1 (по 1 признаку равенства треугольников).
Слайд 15
Повторение материала
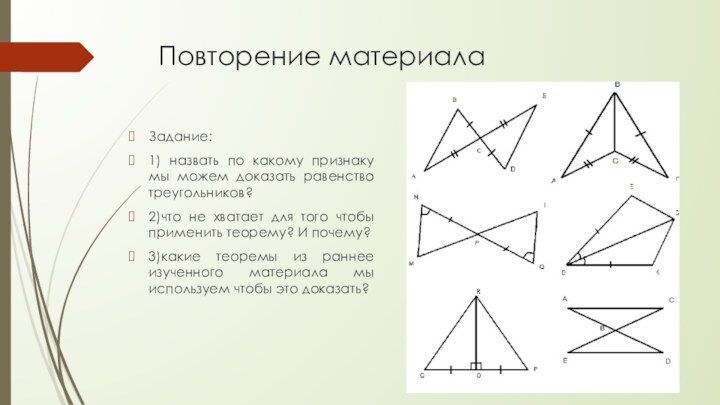
Задание:
1) назвать по какому признаку мы
можем доказать равенство треугольников?
2)что не хватает для того чтобы
применить теорему? И почему?
3)какие теоремы из раннее изученного материала мы используем чтобы это доказать?