a – ____________ , n – ______________.
В
выражении аn a – основание , n – показатель.
основание чётное
нечётное нулю
сумму самому
показатель
- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Конспект урока алгебры в 7 классе по теме Произведение степеней с натуральным показателем
Содержание
- 2. Теоретическая разминка. Вставьте нужное слово.
- 3. Теоретическая разминка. Вставьте нужное слово. В выражении
- 4. Теоретическая разминка. Вставьте нужное слово.Степень с отрицательным
- 5. Теоретическая разминка. Вставьте нужное слово.Степень с отрицательным
- 6. Теоретическая разминка. Вставьте нужное слово.Первая степень любого
- 7. Математическая разминка1. Вспомнить определение степени и расписать
- 8. Eсли a — любое число и m
- 9. Историческая справкаУченики Пифагора изображали числа в виде точек
- 10. Задание 1: Запишите в виде степени
- 11. Задание 2: Заполните пропуски.а) 29 = 23
- 12. Задание 3: Упростите произведение. а)
- 13. Физкультминутка
- 14. Магический квадрат Заполните
- 15. Магический квадрат
- 17. «Пусть кто-нибудь попробует вычеркнуть из математики степени,
- 18. Самостоятельная работа
- 19. Ответы к самостоятельной работе.
- 20. Оценивание работ
- 21. Знание степени числа – это необходимость или лишнее в нашей жизни?
- 22. Приведите примеры, на каких уроках вам встречаются степени и многозначные числа.
- 23. Информатика: 1кБ = 210Б
- 24. Ответь на вопросы, подчеркнув нужные, на
- 25. Домашнее задание:Зашифруйте математический термин , используя знания
- 26. Спасибо за урок !
- 27. Скачать презентацию
- 28. Похожие презентации
Теоретическая разминка. Вставьте нужное слово.
Слайд 3
Теоретическая разминка.
Вставьте нужное слово.
В выражении аn
a – основание , n – показатель.
основание чётное
нечётное нулю
сумму самому
показатель
Слайд 4
Теоретическая разминка.
Вставьте нужное слово.
Степень с отрицательным основанием положительна,
если показатель степени ________ число.
Степень с отрицательным основанием положительна,
если показатель степени чётное число.(- 2)4 = 16
самому чётное
нечётное нулю
сумму
Слайд 5
Теоретическая разминка.
Вставьте нужное слово.
Степень с отрицательным основанием отрицательна,
если показатель степени __________ число.
Степень с отрицательным основанием отрицательна,
если показатель степени нечётное число.(- 2)3 = - 8
нулю
чётное
сумму
нечётное
самому
Слайд 6
Теоретическая разминка.
Вставьте нужное слово.
Первая степень любого числа равна
___________ числу.
Первая степень любого числа равна самому числу.
a1 =
aнулю
сумму
самому
Слайд 7
Математическая разминка
1. Вспомнить определение степени и расписать по
определению следующие степени:
35 =
(- 2)3 =x4 =
2. Записать в виде степени
2∙2∙2∙2∙2 =
с∙с∙с∙с∙с∙с∙с =
(a+b)(a+b)(a+b)(a+b) =
Слайд 8 Eсли a — любое число и m и
n — любые натуральные числа, то
am∙an = aт +
пПравило:
При умножении степеней с одинаковыми основаниями показатели степеней складывают.
Это свойство распространяется на произведение трёх и более степеней.
Пример: Упростите выражение.
y5 y4 y = y5+4+1 = y10
Слайд 9
Историческая справка
Ученики Пифагора изображали числа в виде точек или
выкладывали их из камешков. Квадраты натуральных чисел они называли квадратными
и изображали так:Слайд 10 Задание 1: Запишите в виде степени произведение
степеней.
а) a3 ∙ a7 = …..
(- y)5∙ (-y) = ….. (5 x)6 ∙ (5 x)8 = …..
б) b∙ b4 ∙ b8 = …..
c6 ∙c3 ∙c = …..
(-3a) ∙(-3a)3 ∙(-3a)5 = ……
Слайд 11
Задание 2: Заполните пропуски.
а) 29 = 23 ∙
2...
б) 1010 = 102 ∙ 10…
в) 78 =
75 ∙ …. ....г) 412 = 46 ∙ …. ....
Слайд 12
Задание 3: Упростите произведение.
а) 3a3∙ 7a2
=
б) b4 ∙ 5b8 =
в) 4 x∙ (-0,5x5 ) =
г) (-5a2 ) ∙(-9a) =
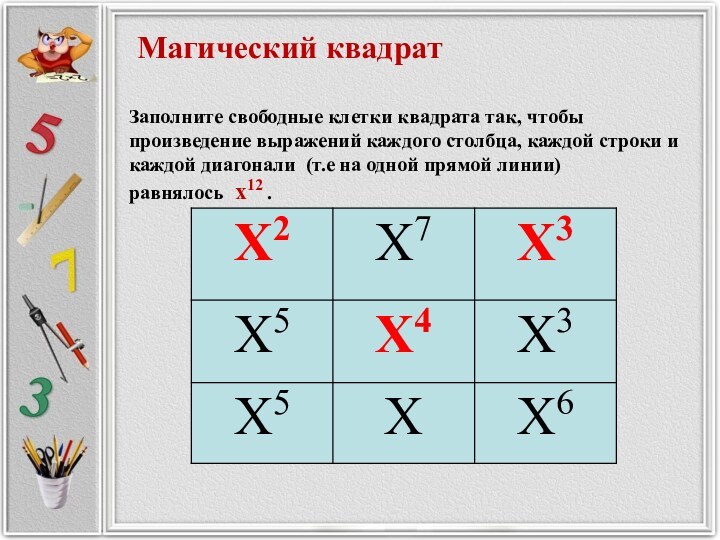
Слайд 14 Магический квадрат Заполните свободные клетки квадрата так,
чтобы произведение выражений каждого столбца, каждой строки и каждой
диагонали (т.е на одной прямой линии) равнялось x12 .Слайд 15 Магический квадрат Заполните свободные клетки квадрата
так, чтобы произведение выражений каждого столбца, каждой строки и
каждой диагонали (т.е на одной прямой линии) равнялось x12 .Слайд 16 «Пусть кто-нибудь попробует вычеркнуть из математики степени,
и он увидит, что без них далеко не уедешь». Задание:
Упростите выражение 1) a2 a3 2) y2(-y)3 (-y) 3) b7b5b2b 4) b2y4 by3 5) y2y y3y8 6) x2x4 x2 x7 7) b3yb2y3 8) a2a4a3 9) ( -x)3(-x)6(-x)7(-x)4Слайд 17 «Пусть кто-нибудь попробует вычеркнуть из математики степени, и
он увидит, что без них далеко не уедешь».
(М. В.Ломоносов)Слайд 23 Информатика: 1кБ = 210Б =
1024 байта
1МБ = 210кБ = 1024 КбайтФизика: Вдавливая кнопку в доску, мы оказываем на нее давление 50 000 000 Па = 5 ∙ 107 Па
Биология: Ежедневно наше тело выделяет от 100 млрд до 100 трлн бактерий или от 1011 до 1014 бактерий.
География: Среднее расстояние от Земли до Солнца ≈ 150 млн км.
Это 150 000 млн м = 1,5 ∙ 1011 м
Слайд 24 Ответь на вопросы, подчеркнув нужные, на твой взгляд
слова. - Понравился ли тебе урок? (Да, нет, не
очень) - Урок для тебя был полезным? (Да, нет, хотелось большего) - Доволен ли ты своими действиями? (Да, нет, не очень) - Как ты оцениваешь свои знания по данной теме? (Отличные, хорошие, плохие, не достаточные) - Покажи, с каким настроением ты уходишь с урока.
Слайд 25
Домашнее задание:
Зашифруйте математический термин , используя знания по
