- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Механические колебания
Содержание
- 2. Цели и задачи:Познакомить учащихся с одним из
- 3. Механические колебания — это движения, которые точно или
- 4. По характеру физических процессов в системе, которые вызывают колебательные движения, различают три основных вида колебаний:свободныевынужденныеавтоколебания
- 5. Группу тел, движение которых мы изучаем, называют
- 6. Свободные колебания – это колебания, которые возникли
- 7. Условия возникновения свободных механических колебаний:1) В одном
- 8. Автоколебаниями называются незатухающие колебания, которые могут существовать
- 9. По характеру изменения во времени кинематических характеристик:Пилообразные;Гармонические;Затухающие.
- 10. Характеристиками колебательного движения - период, частота, амплитуда, фаза колебаний.
- 11. За полный период колебаний тело проходит путь,
- 13. Амплитуда колебаний тела.Амплитудой (А) (лат. amplitude - величина) механических
- 15. Амплитуда скорости – максимально значение скорости колеблющегося тела.Амплитуда
- 16. Уравнение гармонических колебаний- Все гармонические колебания имеют
- 17. Многообразие колебательных процессов естественным образом приводит к
- 19. 1. Колебания в противоположных фазах: Частоты колебаний
- 20. 3. Разность фаз:Ситуации, когда маятники колеблются не
- 21. Свободные колебания пружинного маятникаFx=-kx – закон ГукаFx=max
- 22. Превращение энергии при гармонических колебанияхПотенциальная энергия пружинного
- 23. Затухающие, вынужденные колебания. Любая реальная колебательная система
- 24. Колебания системы, совершающие ею под действием внешней периодической силы, называются вынужденными. Силу, являющейся мерой этого внешнего воздействия, называют вынуждающей.
- 25. РезонансГрафик зависимости амплитуды колебаний от частоты
- 26. В случае резонанса направление вынуждающей силы в
- 27. Обвал Египетского мостаСпособы
- 28. Акустический резонанс Большинство музыкальных инструментов имеет в
- 29. Вопросы для закрепления:1. Какой процесс называют «механические колебания»?
- 30. Задача. Математический маятник длиной 99,5 см за
- 32. Д/З. Учить §18-26
- 33. Скачать презентацию
- 34. Похожие презентации

























Слайд 3 Механические колебания — это движения, которые точно или приблизительно
повторяются через определенные интервалы времени.
Повторяются движения поршней в двигателе
автомобиля, поплавка на волне, ветки дерева на ветру, нашего сердца. Колебаниями называются периодические изменения величин или периодически повторяющиеся движения или процессы.
Слайд 4 По характеру физических процессов в системе, которые вызывают
колебательные движения, различают три основных вида колебаний:
свободные
вынужденные
автоколебания
Слайд 5 Группу тел, движение которых мы изучаем, называют в
механике колебательной системой тел или просто системой.
Силы, действующие между телами системы,
называют внутренними. Внешними силами называют силы, действующие на тела системы со стороны тел, не входящих в нее.
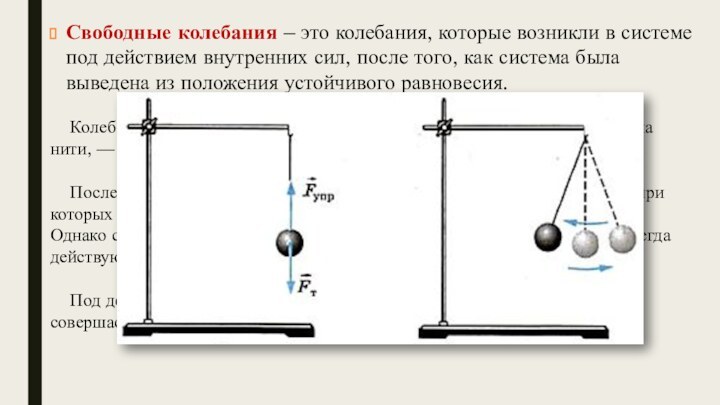
Слайд 6 Свободные колебания – это колебания, которые возникли в
системе под действием внутренних сил, после того, как система
была выведена из положения устойчивого равновесия.Колебания груза, прикрепленного к пружине, или груза, подвешенного на нити, — это примеры свободных колебаний.
После выведения системы из положения равновесия создаются условия, при которых груз колеблется без воздействия внешних сил.
Однако с течением времени колебания затухают, так как на тела системы всегда действуют силы сопротивления.
Под действием внутренних сил и сил сопротивления система совершает затухающие колебания.
Слайд 7
Условия возникновения свободных механических колебаний:
1) В одном определённом
положении тела в пространстве, называемом положением равновесия, равнодействующая сил,
приложенных к телу, должна быть равна нулю. При выведении тела из положения равновесия равнодействующая всех сил должна быть отличной от нуля и направлена к положению равновесия.2) Для начала свободных колебаний система должна быть выведена из положения равновесия внешним воздействием.
3) Силы трения в системе должны быть малы по сравнению с силами, зависящими от координат.
Слайд 8 Автоколебаниями называются незатухающие колебания, которые могут существовать в
системе без воздействия на неё внешних периодических сил и
имеющей источник энергииВынужденные колебания – это колебания, которые происходят под действием внешней, периодически изменяющейся силы.
Качели, которые мы периодически подталкиваем; колебания веток деревьев под действием ветра; колебания проводов линий ЛЭП под действием ветра, колебание маятника часов под действием пружины или груза; струны гитары.
Маятниковые часы, часы с балансиром
Слайд 9
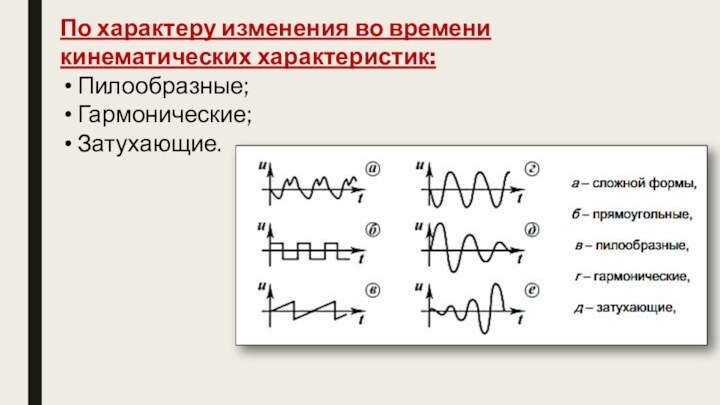
По характеру изменения во времени кинематических характеристик:
Пилообразные;
Гармонические;
Затухающие.
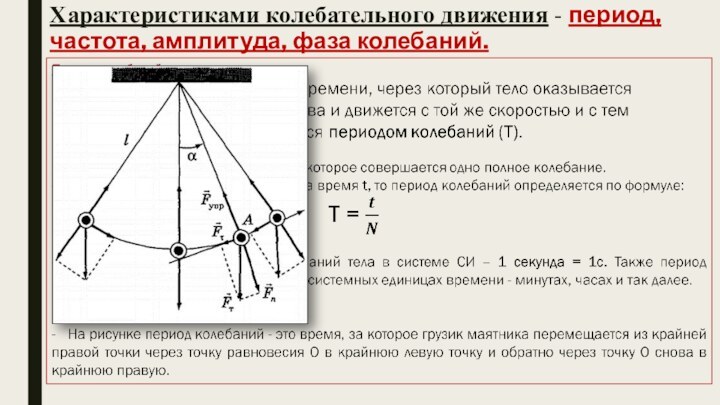
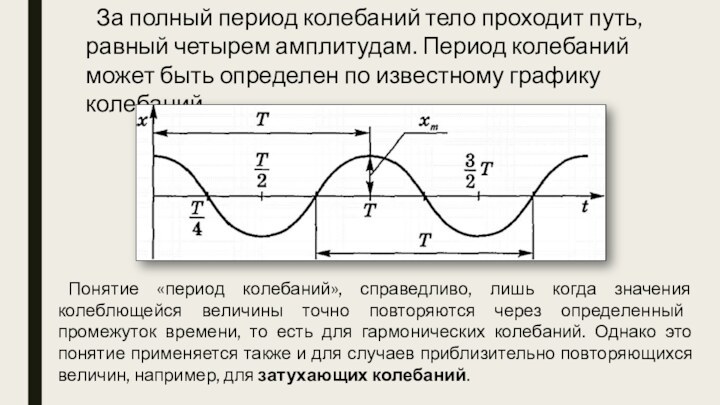
Слайд 11 За полный период колебаний тело проходит путь, равный
четырем амплитудам. Период колебаний может быть определен по известному
графику колебаний,Понятие «период колебаний», справедливо, лишь когда значения колеблющейся величины точно повторяются через определенный промежуток времени, то есть для гармонических колебаний. Однако это понятие применяется также и для случаев приблизительно повторяющихся величин, например, для затухающих колебаний.
Слайд 13
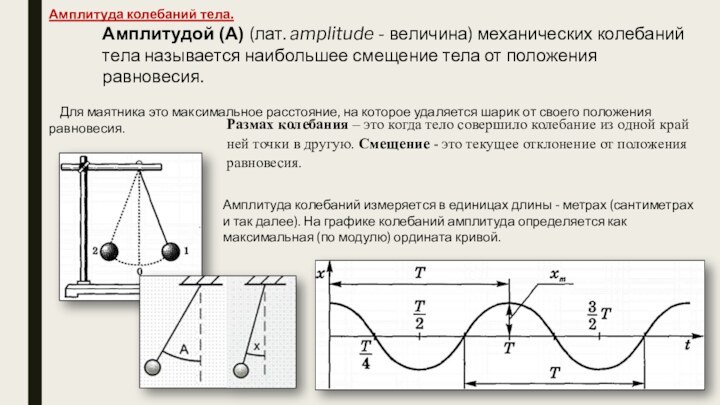
Амплитуда колебаний тела.
Амплитудой (А) (лат. amplitude - величина) механических колебаний
тела называется наибольшее смещение тела от положения равновесия.
Для маятника
это максимальное расстояние, на которое удаляется шарик от своего положения равновесия. Амплитуда колебаний измеряется в единицах длины - метрах (сантиметрах и так далее). На графике колебаний амплитуда определяется как максимальная (по модулю) ордината кривой.
Размах колебания – это когда тело совершило колебание из одной крайней точки в другую. Смещение - это текущее отклонение от положения равновесия.
Слайд 15
Амплитуда скорости – максимально значение скорости колеблющегося тела.
Амплитуда ускорения –
максимальное значение ускорения колеблющегося тела.
Уравнение зависимости скорости и ускорения
от времени:Уравнение зависимости координаты от времени
Уравнение зависимости проекции скорости от времени
Уравнение зависимости проекции ускорения от времени
Слайд 16
Уравнение гармонических колебаний
- Все гармонические колебания имеют математическое
выражение. Их свойства характеризует совокупность тригонометрических уравнений, сложность которых
определяется сложностью самого колебательного процесса, свойствами системы и средой, в которой они происходят, то есть, внешними факторами, воздействующими на колебательный процесс.- Гармонические колебания - это колебания, при которых координата зависит от времени по гармоническому закону: x = х0 * cos (ω * t + α).
- Положительная величина х0 является наибольшим по модулю значением координаты (модуль косинуса равен единице), то есть наибольшим отклонением от положения равновесия. Следовательно, х0 - амплитуда колебаний.
- Аргумент косинуса ωt+α называется фазой колебаний и он определяет место (положение) колеблющейся материальной точки в данный конкретный момент времени при заданной амплитуде.
- Величина а, равная значению фазы при t = 0, называется начальной фазой.
- Начальная фаза отвечает начальной координате тела: а = x0 * cos α.
Слайд 17 Многообразие колебательных процессов естественным образом приводит к тому,
что существует большое количество осцилляторов.
Основные типы:
а) пружинный
осциллятор - обычный груз, обладающий некой массой m, который подвешен на упругой пружине. - Он совершает колебательные движения гармонического типа, которые описываются формулойF = - kx.
б) физический осциллятор (маятник) - твердое тело, совершающее колебательные движения вокруг статичной оси под воздействием определенной силы;
в) математический маятник (в природе практически не встречается). - Он представляет собой идеальную модель системы, включающей колеблющееся физическое тело, обладающее определенной массой, которое подвешено на жесткой невесомой нити.
Слайд 19
1. Колебания в противоположных фазах:
Частоты колебаний
маятников равны между собой, однако их отклонение от положения
равновесия скорости и ускорения в любой момент времени противоположны по знаку и равны по модулю2. Синфазные колебания.
Если же маятники будут колебаться так, что все кинематические величины в любой момент времени будут совпадать и по модулю, и по знаку, то маятники колеблются в одинаковой фазе, то есть синфазно
Слайд 20
3. Разность фаз:
Ситуации, когда маятники колеблются не синфазно
и не противофазно, тогда говорят, что в колебательных системах
присутствует некая разность фазФаза – это величина, которая показывает, на сколько колебания одного маятника опережают или отстают по сравнению с колебаниями второго.
Слайд 21
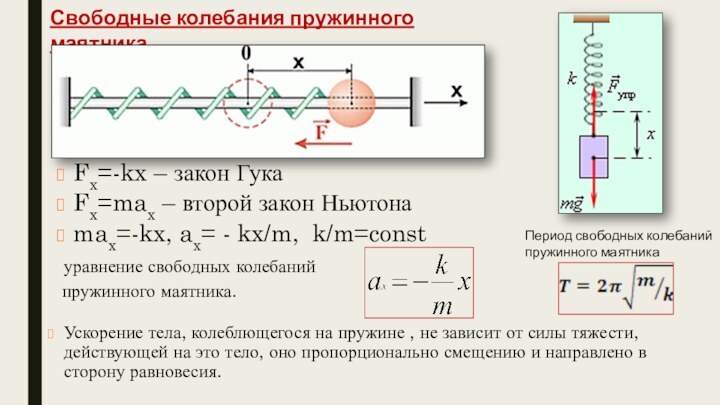
Свободные колебания пружинного маятника
Fx=-kx – закон Гука
Fx=max –
второй закон Ньютона
max=-kx, ax= - kx/m, k/m=const
уравнение свободных
колебанийпружинного маятника.
Период свободных колебаний пружинного маятника
Ускорение тела, колеблющегося на пружине , не зависит от силы тяжести, действующей на это тело, оно пропорционально смещению и направлено в сторону равновесия.
Слайд 22
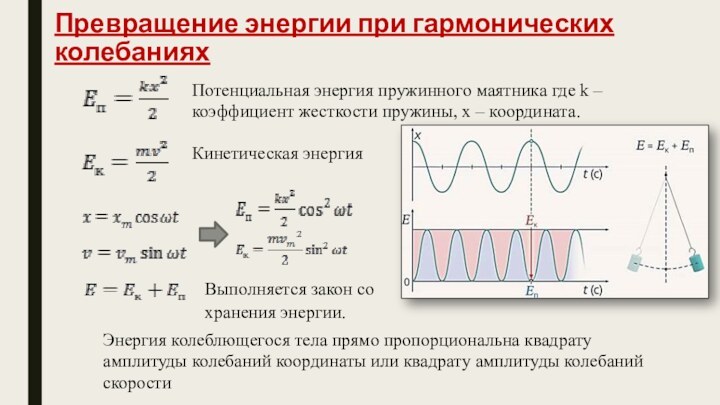
Превращение энергии при гармонических колебаниях
Потенциальная энергия пружинного маятника
где k – коэффициент жесткости пружины, x – координата.
Кинетическая
энергияВыполняется закон сохранения энергии.
Энергия колеблющегося тела прямо пропорциональна квадрату амплитуды колебаний координаты или квадрату амплитуды колебаний скорости
Слайд 23
Затухающие, вынужденные колебания.
Любая реальная колебательная система –
затухающая, так как ей приходится преодолевать силу трения или
силу сопротивления.Колебания затухают, так как влияют два основных фактора: сопротивление воздуха, а также трение в подвесе. Со временем амплитуда становится все меньше, А 0
Во время затухающих колебаний энергия системы непрерывно уменьшается
Слайд 24 Колебания системы, совершающие ею под действием внешней периодической
силы, называются вынужденными.
Силу, являющейся мерой этого внешнего воздействия, называют вынуждающей.
Слайд 25
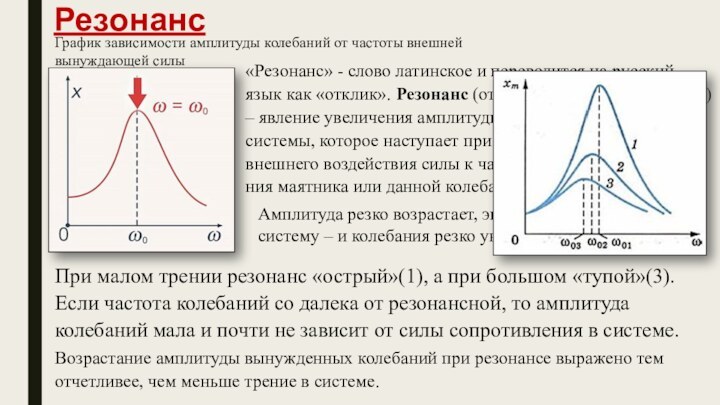
Резонанс
График зависимости амплитуды колебаний от частоты внешней
вынуждающей силы
Амплитуда резко возрастает, энергия резко приходит в
систему – и колебания резко увеличиваются. «Резонанс» - слово латинское и переводится на русский язык как «отклик». Резонанс (от лат. resono – «откликаюсь») – явление увеличения амплитуды вынужденных колебаний системы, которое наступает при приближении частоты внешнего воздействия силы к частоте собственного колебания маятника или данной колебательной системы.
При малом трении резонанс «острый»(1), а при большом «тупой»(3). Если частота колебаний со далека от резонансной, то амплитуда колебаний мала и почти не зависит от силы сопротивления в системе.
Возрастание амплитуды вынужденных колебаний при резонансе выражено тем отчетливее, чем меньше трение в системе.
Слайд 26 В случае резонанса направление вынуждающей силы в любой
момент времени совпадает с направлением движения колеблющегося тела, таким
образом, создаются наиболееблагоприятные условия для пополнения энергии колебательной системы за счет работы вынуждающей силы.
Явление резонанса имеет отношение только к вынужденным колебаниям, то есть когда есть внешняя периодическая вынуждающая сила.
Слайд 27
Обвал Египетского моста
Способы уменьшения
резонанса
Изменения частоты собственных колебаний.
Организация взаимного гашения двух (или
более) вредных действий. Введение второго внешнего действия в противофазе к вредному.
Увеличение сил трения.
Самонейтрализация вредного действия путем введения дополнительных грузов со смещающимся центром тяжести.
Ликвидация источника внешнего действия.
При переходе через мост воинским частям запрещается идти в ногу. Строевой шаг приводит к периодическому воздействию на мост. Если случайно частота этого воздействия совпадет с собственной частотой колебаний моста, то он может разрушиться.
Слайд 28
Акустический резонанс
Большинство музыкальных инструментов имеет в своем
устройстве резонатор - устройство для усиления и продления издаваемых
звуков. Акустическими резонаторами являются например, струны и корпус скрипки, трубка у флейты, корпус у барабанов, а так же комнаты, залы или их отдельные части. Голосовой аппарат человека так же является резонатором.
Слайд 29
Вопросы для закрепления:
1. Какой процесс называют «механические колебания»?
2.
Какой процесс называют «свободные колебания»?
3. Какие процессы называют «вынужденные
колебания, автоколебания»?4. Какую характеристику колебаний называют «периодом колебаний»?
5. Какую характеристику колебаний называют «частотой колебаний»?
6. Какую характеристику колебаний называют «амплитудой колебаний»?
7. Какую характеристику колебаний называют «фазой колебаний»?
8. Какие колебания называют гармоническими колебаниями?
9. Какую систему называют математическим маятником?
10. Свободные колебания пружинного маятника?
11. Что представляет собой явление резонанса?