Слайд 2
Содержание:
Что такое комбинаторика?
Пример 1
Пример 2
Задачи
Перестановки
Сочетания
Размещения
Слайд 3
Что такое комбинаторика?
Задачи , решая которые приходится составлять
различные комбинации из конечного числа элементов и подсчитывать число
комбинаций , называются комбинаторными.
Раздел математики , в котором рассматриваются подобные задачи, называют комбинаторикой.
Слово «комбинаторика» от латинского combinare - «соединять , сочетать».
Слайд 4
Пример 1
Из группы теннисистов, в которую входят четыре
человека - Антонов, Григорьев , Сергеев и Федоров, тренер
выделяет пару для участия в соревнованиях. Сколько существует вариантов выбора такой пары?
АГ, АС, АФ
ГС, ГФ
СФ
Значит, всего существует шесть вариантов выбора.
Способ рассуждений , которым мы воспользовались , называют перебором возможных вариантов.
Слайд 5
Пример 2
Сколько трехзначных чисел можно составить из цифр
1, 3, 5, 7,используя в записи числа каждую из
них не более
одного раза?
Чтобы ответить на вопрос задачи , выпишем все такие числа . Полученные результаты запишем в четыре строки , в каждой из которых шесть чисел:
135 137 153 157 173 175
315 317 351 357 371 375
513 517 531 537 571 573
713 715 731 735 751 753
Слайд 6
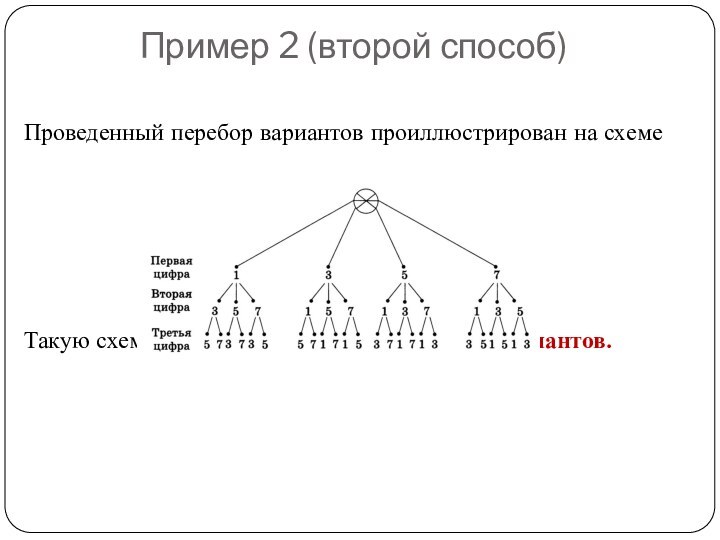
Проведенный перебор вариантов проиллюстрирован на схеме
Такую схему называют
деревом возможных вариантов.
Пример 2 (второй способ)
Слайд 7
Первую цифру можно выбрать четырьмя способами. Так как
после выбора первой цифры останутся три , то вторую
цифру можно выбрать уже тремя способами. Наконец , третью цифру можно выбрать двумя способами. Следовательно , общее число искомых чисел равно произведению 4*3*2,т.е.24.
Использовалось комбинаторное правило умножения.
Пример 2 (третий способ)
Слайд 8
Комбинаторное правило умножения
Пусть имеется n элементов и требуется
выбрать из них один за другим k элементов. Если
первый элемент можно выбрать n1 способами, после чего второй элемент можно выбрать n2 способами из оставшихся, затем третий элемент можно выбрать n3 способами из оставшихся и т. д., то число способов, которыми могут быть выбраны все k элементов, равно произведению n1 · n2 · n3 · … · nk.
Слайд 9
Задачи
Пример 1. Из города А в город В
ведут две дороги, из города В в город С
– три дороги , из города С до пристани-две дороги. Туристы хотят проехать из города А через В и С к пристани. Сколькими способами они могут выбрать маршрут?
Пример 2. В кафе предлагают два первых блюда: борщ, рассольник - и четыре вторых блюда: гуляш, котлеты, сосиски, пельмени. Укажите все обеды из двух блюд, которые может заказать посетитель. Построить дерево возможных вариантов.
Слайд 10
Перестановки
Перестановкой называется какой-либо способ упорядочения данного множества.
Чтобы
найти число всех перестановок множества из n предметов (это число обозначается Pn,
от французского permutation – перестановка) – например, число способов, которыми можно расставить n томов на книжной полке, – обычно рассуждают таким образом.
Слайд 11
Первым можно поставить любой из n предметов, вторым – любой
из (n – 1) оставшихся предметов, третьим любой из (n – 2)
оставшихся предметов и т. д. В результате число перестановок будет равно произведению n множителей n (n – 1) (n – 2) ... ∙ 3 ∙ 2 ∙ 1.
Для произведения первых n натуральных чисел используют специальное обозначение: n! ( читается n факториал).
Перестановки
Слайд 12
Задачи
Пример 1. Сколькими способами могут быть расставлены 8
участниц финального забега на восьми беговых дорожках?
Пример 2. Сколько
различных четырехзначных чисел, в которых цифры не повторяются, можно составить из цифр 0, 2, 4, 6?
Слайд 13
Сочетания
Сочетанием из n элементов по k называется комбинация,
в которой из этих n элементов выбраны любые k
без учета их порядка в комбинации.
Таким образом, для сочетания имеет значение только состав выбранных элементов, а не их порядок.
Слайд 14
Задачи
Пример 1. Из 15 членов туристической группы надо
выбрать трех дежурных. Сколькими способами можно сделать этот выбор?
Пример
2. Из вазы с фруктами, в которой лежит 9 яблок и 6 груш, надо выбрать 3 яблока и 2 груши. Сколькими способами можно сделать такой выбор?
Слайд 15
Размещения
Размещением из n элементов по k называется комбинация,
в которой какие-то k из этих n элементов расположены
в определенном порядке.
Размещения отличаются друг от друга не только порядком расположения элементов, но и тем, какие именно k элементов выбраны в комбинацию.
Слайд 16
Различия между перестановками, размещениями и сочетаниями
В случае перестановок
берутся все элементы и изменяется только их местоположение.
В случае
размещений берётся только часть элементов и важно расположение элементов друг относительно друга.
В случае сочетаний берётся только часть элементов и не имеет значения расположение элементов друг относительно друга.