Презентация на тему с элементами анимации по технической механике по теме Плоская система сходящихся сил

точке
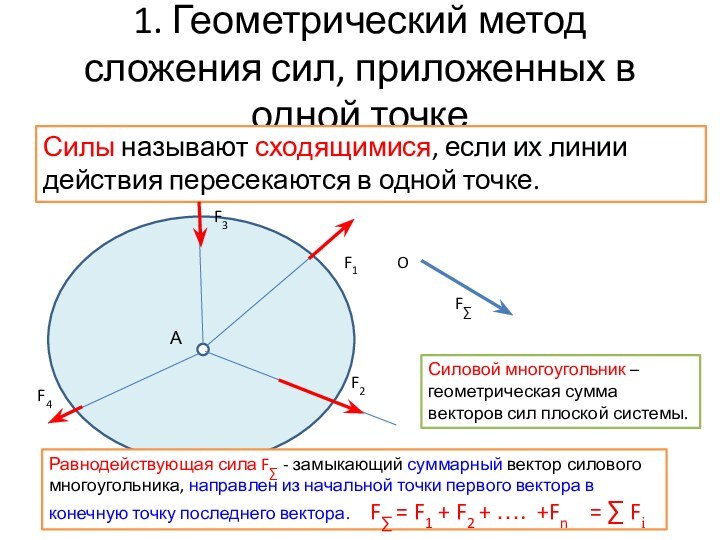
Силы называют сходящимися, если их линии действия пересекаются в

А

F1

F4

F3

F2

O

F∑

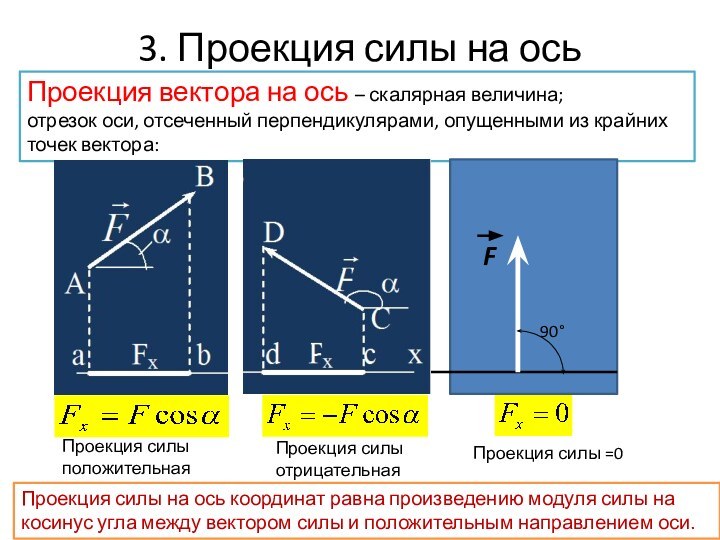
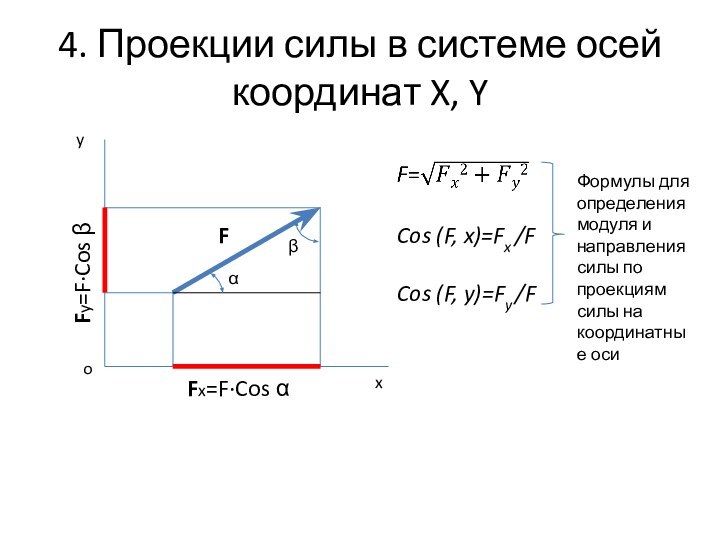
Силовой многоугольник – геометрическая сумма векторов сил плоской системы.

Равнодействующая сила F∑ - замыкающий суммарный вектор силового многоугольника, направлен из начальной точки первого вектора в конечную точку последнего вектора. F∑ = F1 + F2 + …. +Fn = ∑ Fi

силового многоугольника конечная точка последней слагаемой силы совместится с

F1

F2

F3

F4

F∑ = 0 результирующая сила = 0
(суммарный вектор системы сил = 0) =>

=> система сходящихся сил находится в равновесии.

Самозамыкание силового многоугольника данной ПССС является геометрическим условием её равновесия.

силой данной системы:
OA
AB
BC
CD
OD

сходящихся сил:
Рис. 1
Рис. 2
Рис. 3
Рис. 1
Рис. 2
Рис. 3

– скалярная величина;
отрезок оси, отсеченный перпендикулярами, опущенными из

Проекция силы положительная

Проекция силы отрицательная

Проекция силы =0

Проекция силы на ось координат равна произведению модуля силы на косинус угла между вектором силы и положительным направлением оси.

Y
x
y
o
F
Fy=F∙Cos β
Fx=F∙Cos α
α
β
Cos (F, x)=Fx /F

Cos (F, y)=Fy

Формулы для определения модуля и направления силы по проекциям силы на координатные оси

равновесии, когда алгебраические суммы проекций её слагаемых на каждую

в точке В подвешены два груза (груз G1= 600

Ответ: R1=1166 H (стержень АВ растянут), R2= - 1249 H (стержень ВС сжат).

Алгоритм:
схема сил и реакций;
направление осей Х, У;
система уравнений равновесия;
определяем реакции.