- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему урока по математике 8 класс на тему: Свойства числовых неравенств
Содержание
- 2. 1. Сравните числа:
- 3. 2. Не выполняя вычислений, сравните значения выражений:
- 4. 3. Сравните выражения:
- 5. Разминка для глаз
- 6. Тема урока:Числовые неравенства и их свойства
- 7. Цели: изучить теоремы, выражающие
- 8. Задание 1. Сравните числа:а) 5,1 и 2,5;
- 9. Вывод:Если a > b, то b…а.Если а < b, то b…а.
- 10. Теорема 1.Если а > b, то b
- 11. Геометрическая иллюстрация этого свойства приведена на рисунках.Если
- 12. Задание 2. Сравните числа:a)2,3 и 7,6;
- 13. Вывод:Если a < b и b < с, то a…c.
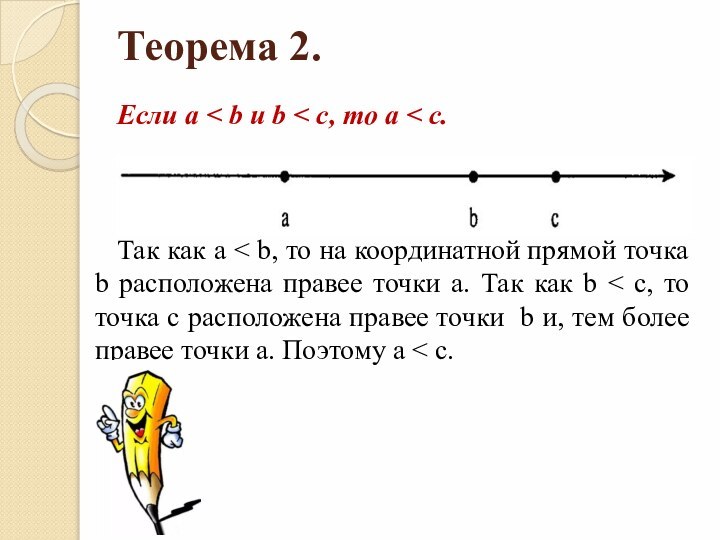
- 14. Теорема 2.Если а < b и b
- 15. Задание 3. Сравните:
- 16. Вывод:Если a < b, то a+c…b+c.
- 17. Теорема 3.Если a < b и с
- 18. Задание 4. Сравните:а) 11,1 и 12,1;б) 0,7
- 19. Вывод:Если a < b и c > 0, то ac…bc.
- 20. Сравните:а) 11,1 и 12,1;б) 0,7 и 1;в)
- 21. Вывод.Если a < b и c < 0, то ab…bc
- 22. Теорема 4.Если a < b и с
- 23. Следствие.
- 24. Пример 1Известно, что a
- 25. Пример 2
- 26. Пример 3.Оценим периметр квадрата со стороной а см, если известно, что 18,1 < a < 18,2.
- 27. Решите: № 746, 749
- 28. Релаксация- Сформулируйте основные свойства числовых неравенств.- Если
- 29. Домашнее задание: п. 29 № 747, 751, 752, 753
- 30. Литература:Алгебра . 8 класс: учеб. для общеобразоват.
- 31. Скачать презентацию
- 32. Похожие презентации
1. Сравните числа:
















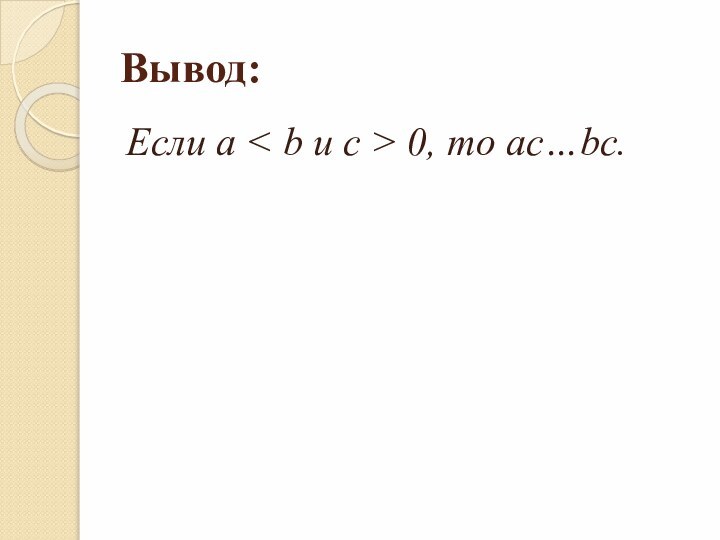












Слайд 7 Цели: изучить теоремы, выражающие свойства
числовых неравенств; формировать умение применять теоремы–свойства при решении задач.
Слайд 8
Задание 1. Сравните числа:
а) 5,1 и 2,5;
б)
-3 и 2;
в) 1,05 и 1,0005;
2,5 и 5,1;
2 и
-3;1,0005 и 1,05.
Слайд 10
Теорема 1.
Если а > b, то b
a и если a < b, то b >
a.Доказательство:
если а > b, то по определению разность а-b > 0. Но тогда величина b-a < 0, что по определению означает
b < a.
Если а < b, то по определению разность а-b < 0. Но тогда величина b-a > 0, что по определению означает
b > a.
Теорема доказана.
Слайд 11
Геометрическая иллюстрация этого свойства приведена на рисунках.
Если а
> b, то на координатной прямой точка а расположена
правее точки b. Но тогда точка b расположена левее точки а, что и означает b < a.Если а < b, то на координатной прямой точка а расположена левее точки b. Но тогда точка b расположена правее точки а, что и означает b > a.
Слайд 12
Задание 2. Сравните числа:
a)2,3 и 7,6;
7,6 и 8,7;
2,3 и 8,7;б)-,1,5 и -1,25; -1,25 и -1; -1,5 и -1;
в)-0,7 и 2; 2 и 2,1; - 0,7 и 2,1.
Слайд 14
Теорема 2.
Если а < b и b
с, то а < с.
Так как а
b, то на координатной прямой точка b расположена правее точки а. Так как b < с, то точка с расположена правее точки b и, тем более правее точки а. Поэтому а < с.
Слайд 17
Теорема 3.
Если a < b и с –
любое число, то а+с < b +с.
Так как а
< b, то точка а расположена на координатной оси левее точки b. Точка а+с смещена относительно точки а на такое же расстояние, как и точка b+с относительно точки b. Поэтому точка а+с расположена на координатной оси левее точки b+с и, следовательно, а+с < b +с.
Итак, если к обеим частям верного неравенства прибавить одно и то же число, то получится верное неравенство.
Слайд 18
Задание 4. Сравните:
а) 11,1 и 12,1;
б) 0,7 и
1;
в) 0,01 и 0,001;
11,1∙3 и 12,1 ∙ 3;
0,7 ∙
1,1 и 1 ∙ 1,1;0,01 ∙ 10 и 0,001 ∙ 10.
Слайд 20
Сравните:
а) 11,1 и 12,1;
б) 0,7 и 1;
в) 0,01
и 0,001;
11,1 ∙(-3) и 12,1 ∙(-3);
0,7 ∙(-1,1) и 1
∙(-1,1);0,01 ∙(-10) и 0,001 ∙(-10).
Слайд 22
Теорема 4.
Если a < b и с –
положительное число, то ac < bc. Если a
b и с – отрицательное число, то ac > bc.Так как деление можно заменить умножением на число, обратное делению, то свойство, аналогичное рассмотренному, справедливо и для деления.
Итак, если обе части верного неравенства умножить или разделить на одно и тоже положительное число, то получится верное неравенство. Если обе части верного неравенства умножить или разделить на одно и тоже отрицательное число и при этом изменить знак неравенства на противоположный, то получится верное неравенство.
Слайд 28
Релаксация
- Сформулируйте основные свойства числовых неравенств.
- Если к
обеим частям верного неравенства прибавить отрицательное число, то получится
ли верное неравенство?- Можно ли обе части верного неравенства умножить на отрицательное число, чтобы получилось верное неравенство?
Какое ещё условие необходимо соблюсти?
- Если a4. Можно ли утверждать, что a>4?
Слайд 30
Литература:
Алгебра . 8 класс: учеб. для общеобразоват. организаций
/ Ю.Н. Макарычев, Н.Г. Миндюк, К.И. Нешков, С.В. Суворова:
под ред. С.А. Теляковского. – 4-е изд. – М.: Просвещение, 2015. – 287с.Алгебра . 8 класс: поурочные планы по учебнику Ю.Н. Макарычева, Н.Г. Миндюк, К.И. Нешкова, С.В. Суворовой /авт.-сост. Т.Ю. Дюмина, А.А. Махонина. – Волгоград: Учитель. 2011 – 399 с.





























