- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Урок на тему Построение графиков функций путем преобразования
Содержание
- 2. Цели урока: Повторить способы преобразования графиков функций.Проверить знания учащихся.
- 3. Преобразования:y = f(x – a)y = f(x)
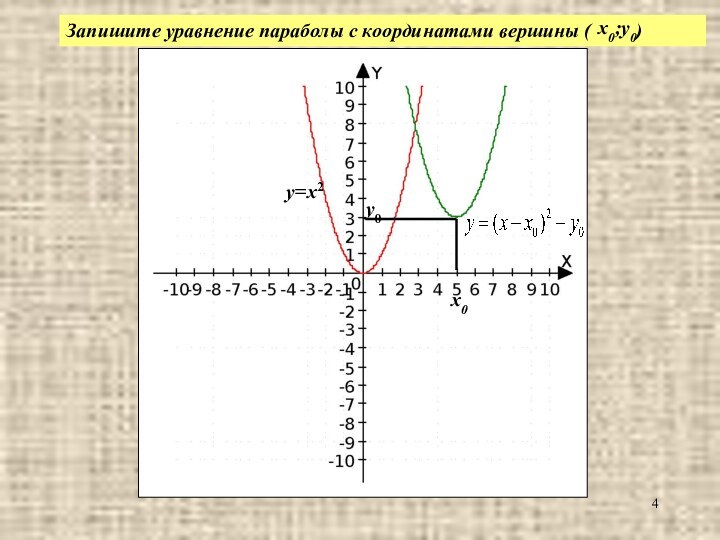
- 4. y=x2y0x0Запишите уравнение параболы с координатами вершины ( )x0;y0
- 5. 1. Параллельный перенос (сдвиг).Рассмотрим параллельный перенос вдоль
- 6. График функции y = f (x -
- 7. Ясно, что если а
- 8. Пример 1. График функции y = (x
- 9. Пример 2. График функции
- 10. Рассмотрим теперь параллельный перенос вдоль оси ординат.
- 11. y =3xy=3x - 1Пример 3. Чтобы построить
- 12. Пример 4. Чтобы построить график функции
- 13. ТестВопрос 1.График функции (зеленый) получен из графика
- 14. Вопрос 2.График функции (зеленый) получен из графика
- 15. 1.2.3.4.График функции получен из данного с помощью
- 16. 2. Деформация (растяжение и сжатие) графика. График
- 17. y=sin xy=sin 2xПример 5. График функции y
- 18. Пример 6. График функции
- 19. y = f(x)y = 2·f(x)Пример 7. График
- 20. Пример 8. График функции
- 21. y = f(x)y = -f(x)ху3. Отражение. График
- 22. y = f(x)хуГрафик функции y = f(-x)
- 23. График функции y=|f(x)| получается из графика функции
- 24. y= f (|x|);y=f(| x |) – четная
- 25. Замечание. Нетрудно показать, что если у
- 26. Скачать презентацию
- 27. Похожие презентации
Цели урока: Повторить способы преобразования графиков функций.Проверить знания учащихся.









Слайд 3
Преобразования:
y = f(x – a)
y = f(x) +
b
y = - f(x)
y = f(-x)
y = kf(x), где
k>0y = f(kx), где k>0
y = |f(x)|
y = f(|x|)
Слайд 5
1. Параллельный перенос (сдвиг).
Рассмотрим параллельный перенос вдоль оси
абсцисс. Пусть дан график функции y = f(x). Как
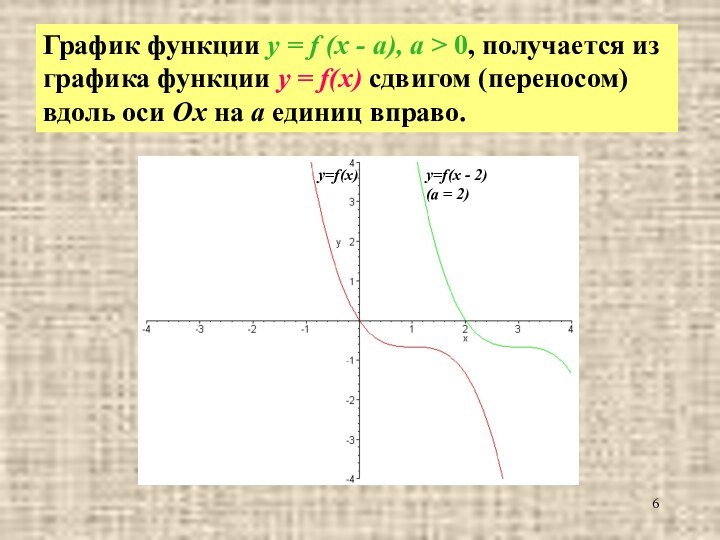
по отношению к нему будет расположен график функции y = f(x – a), a>0 ?Слайд 6 График функции y = f (x - a),
a > 0, получается из графика функции y =
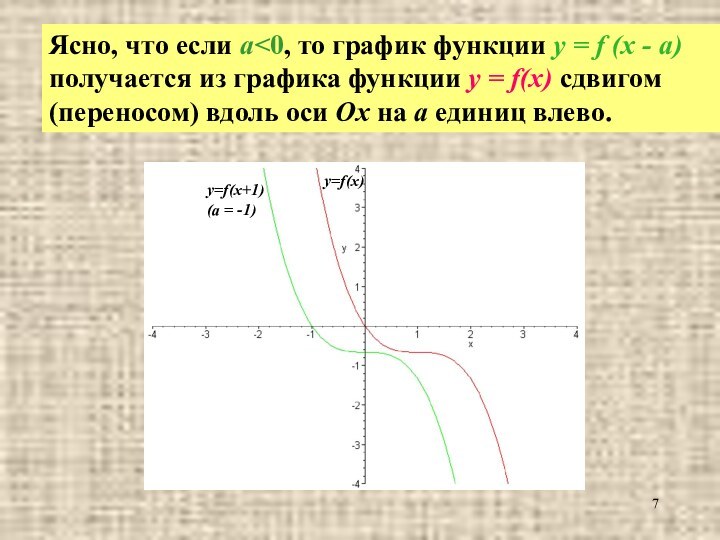
f(x) сдвигом (переносом) вдоль оси Ох на а единиц вправо.Слайд 7 Ясно, что если а
= f (x - a) получается из графика функции
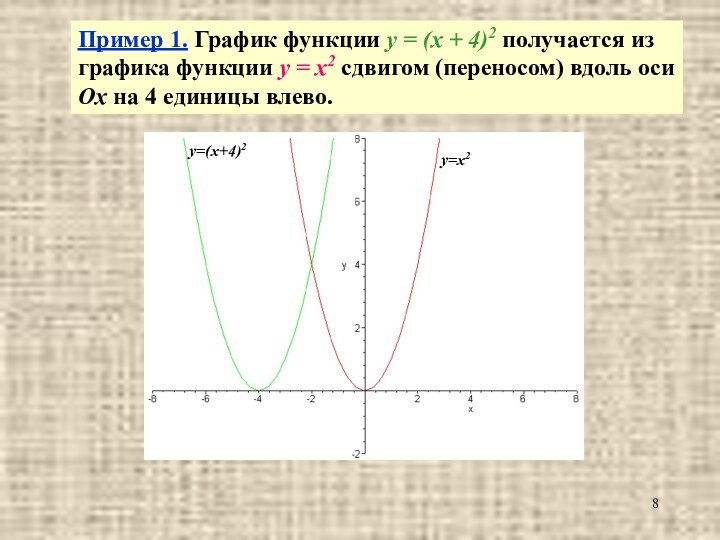
y = f(x) сдвигом (переносом) вдоль оси Ох на а единиц влево.Слайд 8 Пример 1. График функции y = (x +
4)2 получается из графика функции y = x2 сдвигом
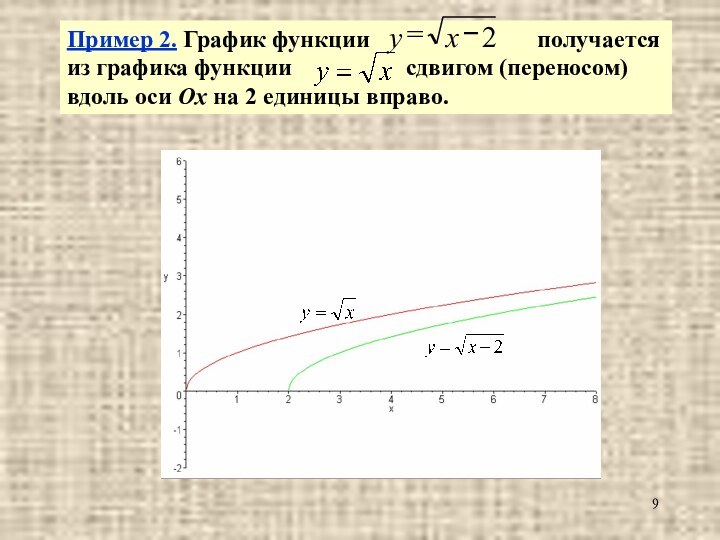
(переносом) вдоль оси Ох на 4 единицы влево.Слайд 9 Пример 2. График функции
получается из графика функции сдвигом (переносом) вдоль оси Ох на 2 единицы вправо.
Слайд 10 Рассмотрим теперь параллельный перенос вдоль оси ординат. В
этом случае график функции y = f(x) + b
получается из графика функции y=f(x) при b > 0 смещением на b единиц вверх, а при b < 0 – на |b| единиц вниз.
Слайд 11
y =3x
y=3x - 1
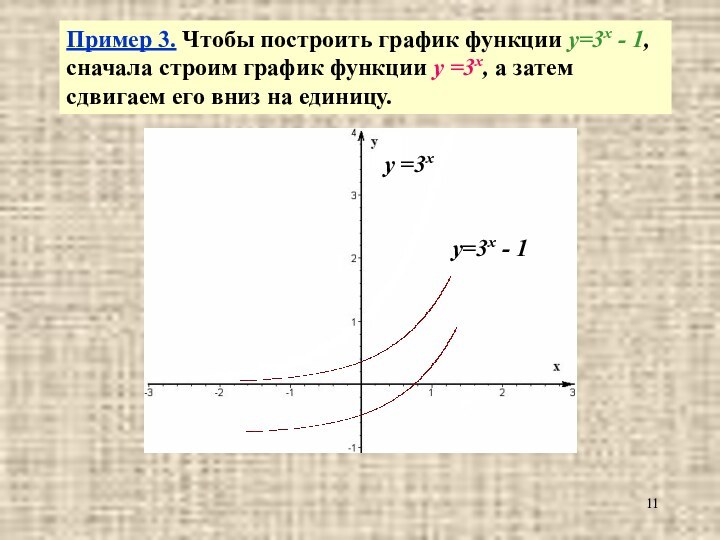
Пример 3. Чтобы построить график
функции y=3x - 1, сначала строим график функции y
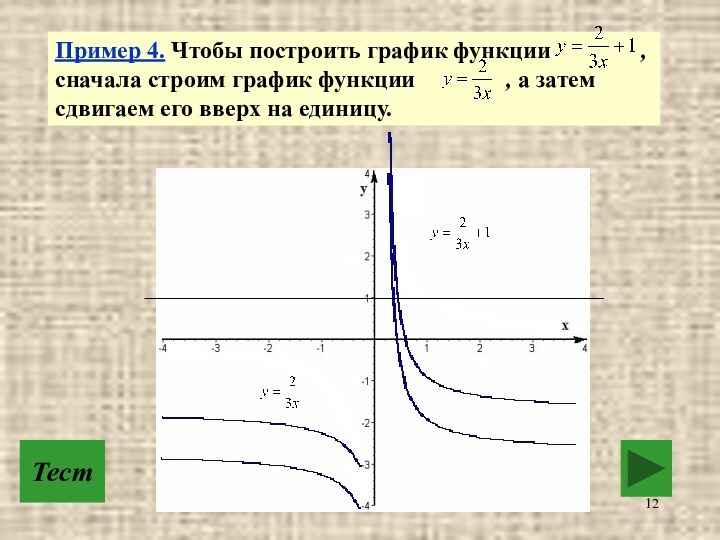
=3x, а затем сдвигаем его вниз на единицу.Слайд 12 Пример 4. Чтобы построить график функции
, сначала строим график
функции , а затем сдвигаем его вверх на единицу.Тест
Слайд 13
Тест
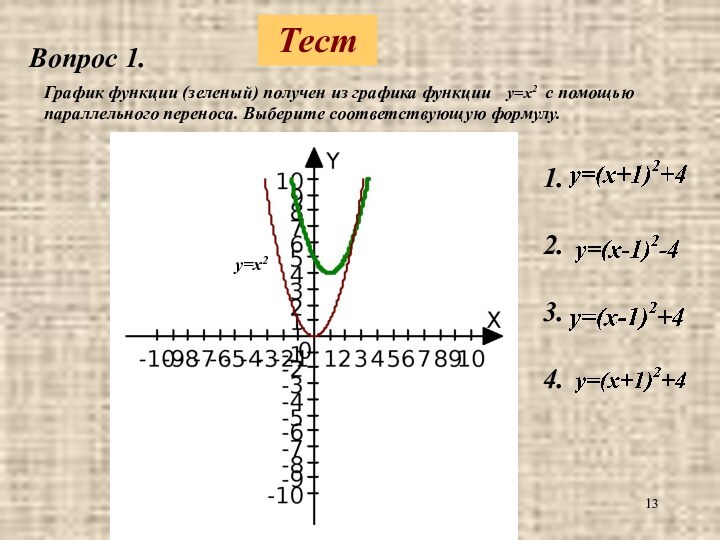
Вопрос 1.
График функции (зеленый) получен из графика функции
с помощью параллельного переноса.
Выберите соответствующую формулу.y=x2
1.
2.
3.
4.
y=x2
Слайд 14
Вопрос 2.
График функции (зеленый) получен из графика функции
с помощью параллельного переноса.
Выберите соответствующую формулу.y=x3
1.
2.
3.
4.
y=x3
Слайд 15
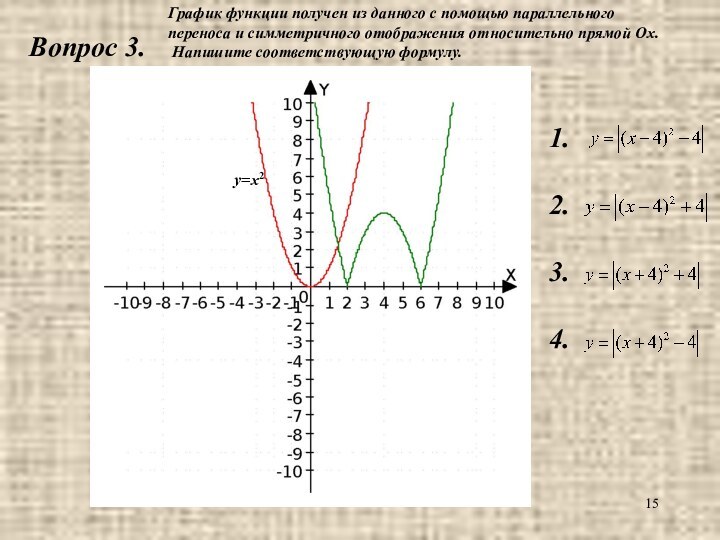
1.
2.
3.
4.
График функции получен из данного с помощью параллельного
переноса и симметричного отображения относительно прямой Ох.
Напишите соответствующую
формулу.Вопрос 3.
Слайд 16
2. Деформация (растяжение и сжатие) графика.
График функции
у = f(ω·x), ω > 0 ,
получается из графика функции у = f(x), «сжатием» к оси у в ω раз при ω > 1 и «растяжением» от оси у в раз при 0 < ω < 1.График функции у = k·f(x), k > 0 , получается из графика функции у = f(x), «растяжением» от оси х в k раз при k > 1 и «сжатием» к оси х в раз при
0 < k <1. Замечание.
Показать
Показать
Слайд 17
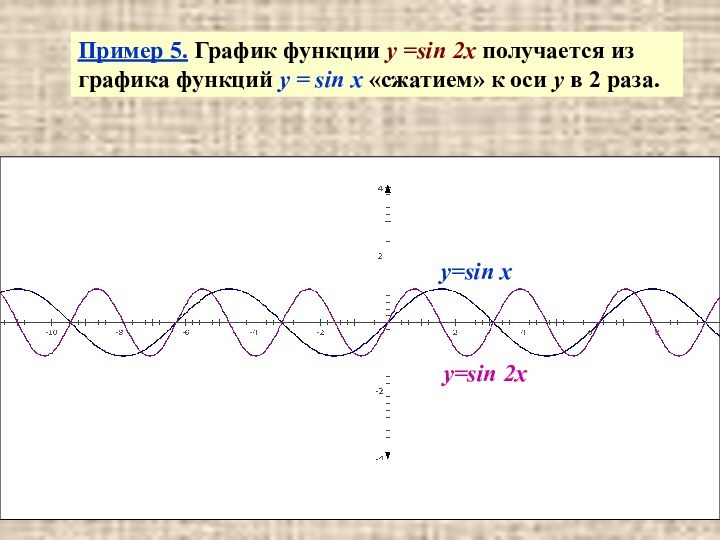
y=sin x
y=sin 2x
Пример 5. График функции y =sin
2x получается из графика функций y = sin x
«сжатием» к оси у в 2 раза.
Слайд 18
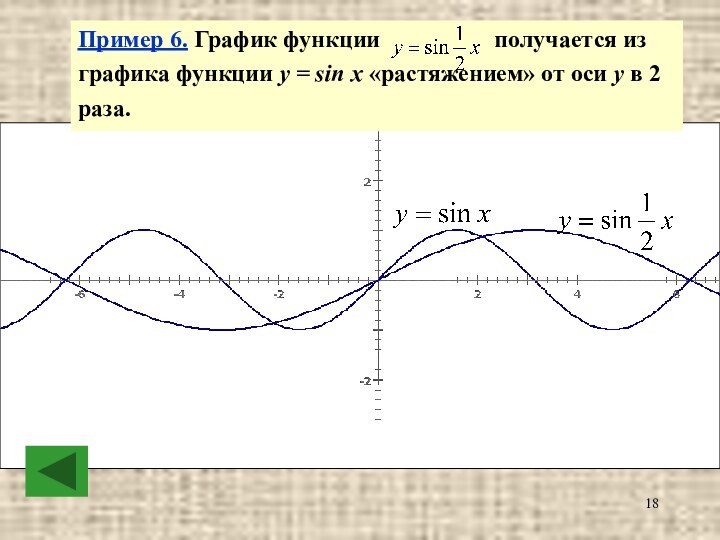
Пример 6. График функции
получается из графика функции
y = sin x «растяжением» от оси у в 2 раза.
Слайд 19
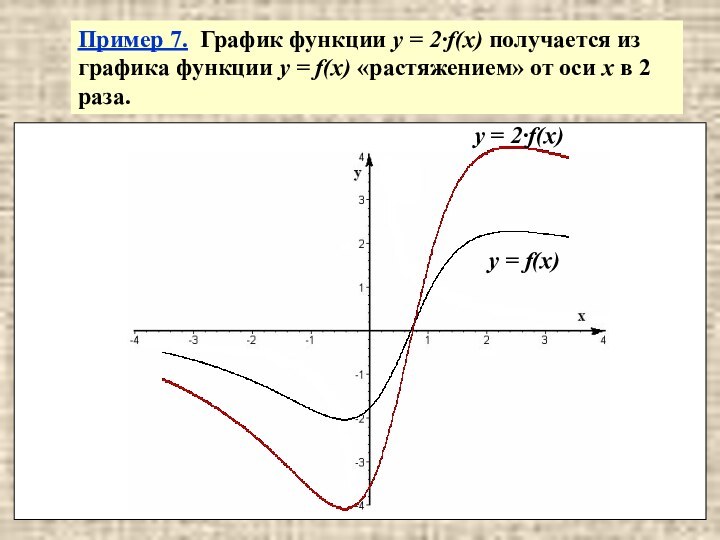
y = f(x)
y = 2·f(x)
Пример 7. График функции
y = 2·f(x) получается из графика функции y =
f(x) «растяжением» от оси х в 2 раза.
Слайд 20
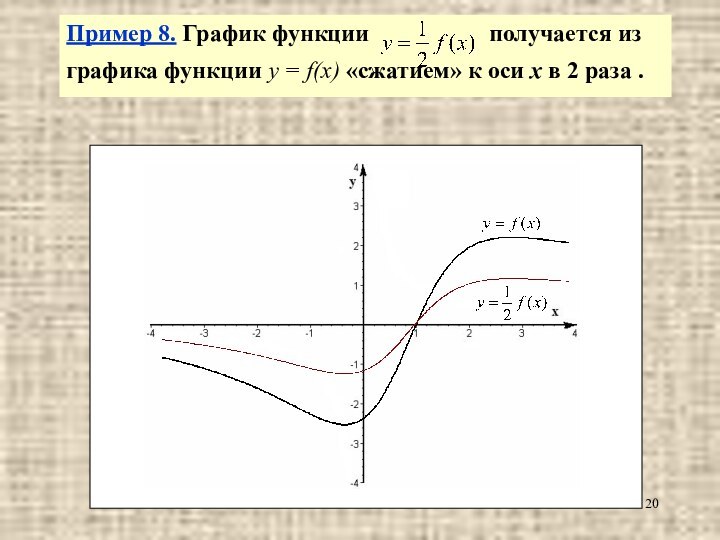
Пример 8. График функции
получается из графика функции
y = f(x) «сжатием» к оси х в 2 раза .
Слайд 21
y = f(x)
y = -f(x)
х
у
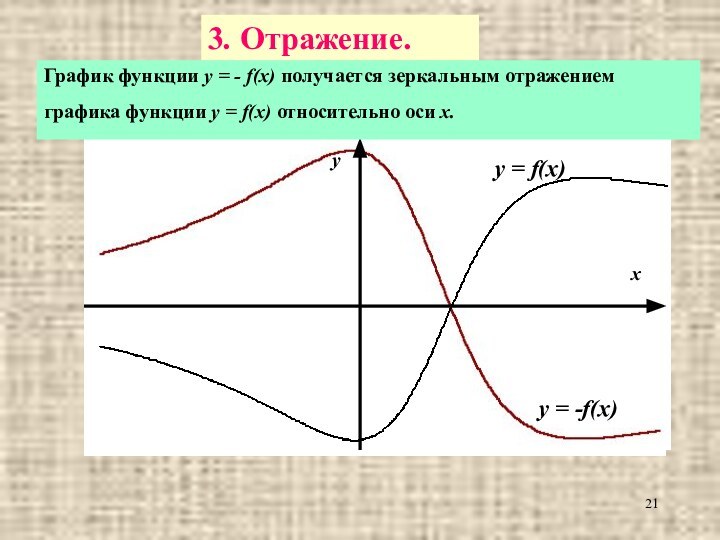
3. Отражение.
График функции
y = - f(x) получается зеркальным отражением графика функции
y = f(x) относительно оси х.
Слайд 22
y = f(x)
х
у
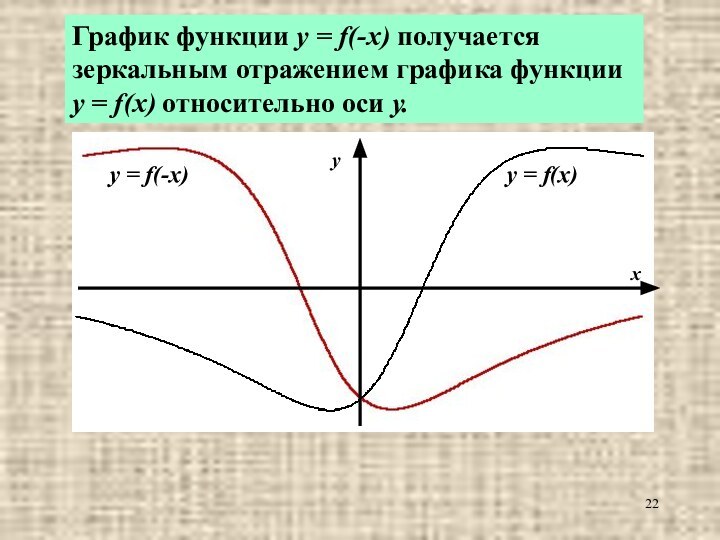
График функции y = f(-x) получается
зеркальным отражением графика функции y = f(x) относительно оси
у.y = f(-x)
Слайд 23
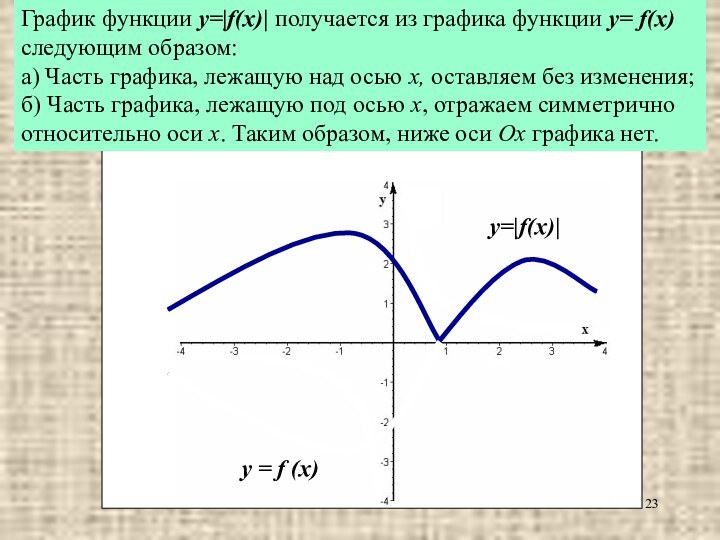
График функции y=|f(x)| получается из графика функции y=
f(x) следующим образом:
а) Часть графика, лежащую над осью
x, оставляем без изменения;б) Часть графика, лежащую под осью x, отражаем симметрично относительно оси x. Таким образом, ниже оси Ox графика нет.
y = f (x)
y=|f(x)|
Слайд 24
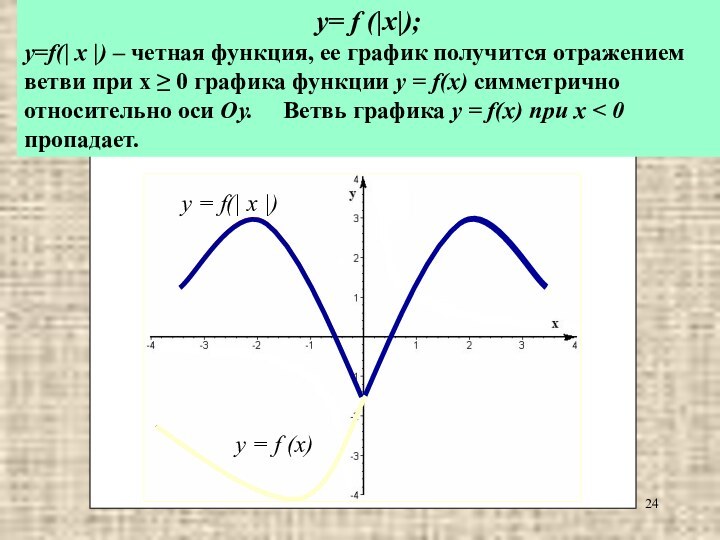
y= f (|x|);
y=f(| x |) – четная функция,
ее график получится отражением ветви при x ≥ 0
графика функции y = f(x) симметрично относительно оси Оу. Ветвь графика y = f(x) при х < 0 пропадает.y = f (x)
у = f(| x |)
Слайд 25
Замечание.
Нетрудно показать, что если у =
f(x) − периодическая функция с периодом Т, то функция
у = f(ω·x), ω > 0, является периодической с периодом . В самом деле, так как функция f(x) имеет период Т, то при любом х выполняется равенство f(x + T) = f(x). Положим φ(x)=f(ω·x) ; тогда для любого х получими, следовательно, функция φ(x) имеет период .
Например, функция y = sin2x имеет период , а функция − период .





























