- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Урок на тему Способы задания функции
Содержание
- 2. «Когда математика стала изучатьпеременные величины и функции,как
- 3. Температура воздуха в течение суток
- 4. Вы пришли в магазин купить конфеты.
- 5. Классная работа. Способы задания функции
- 6. Функция считается заданной, если указаны её область
- 7. Описательный способ задания функции. Каждому однозначному натуральному
- 8. Способ задания функции с помощью формулы.Функция задана формулой У=2ХФункция задана формулой У=Х-5С=150К
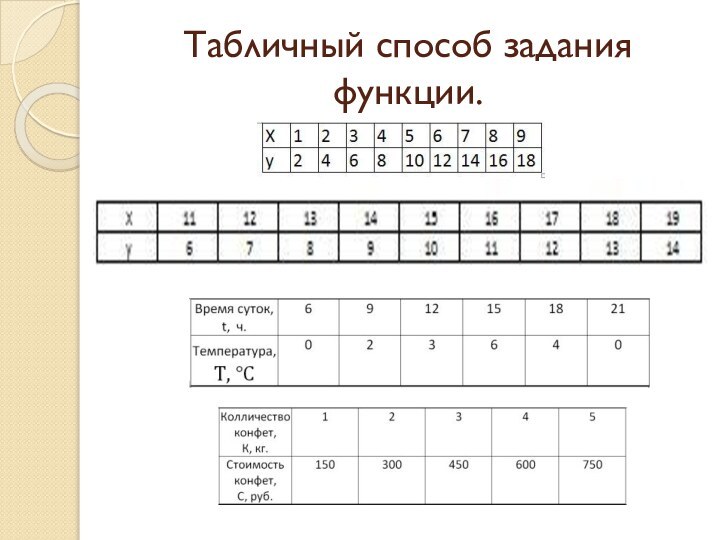
- 9. Табличный способ задания функции.
- 10. ФизкультминуткаСколько?Сколько функций на картинках, столько приседаем.Сколько здесь
- 11. Числа Фибоначчи0, 1, 1, 2, 3, 5,
- 12. Золотое сечение
- 13. Самостоятельная работа
- 14. Ответим вместе! Какую цель в начале урока
- 15. Оцени себяНа уроке мне было всё понятно.
- 16. Домашнее заданиеОбязательная часть: параграф 21, вопросы 1,
- 17. Скачать презентацию
- 18. Похожие презентации
«Когда математика стала изучатьпеременные величины и функции,как только она научиласьописывать процессы, движение,так она стала необходима всем».
















Слайд 2
«Когда математика стала изучать
переменные величины и функции,
как только
она научилась
Ф.Энгельс
Слайд 3
Температура воздуха в течение суток
меняется
в зависимости от времени, в 6 часов - 0
℃в 9 часов - 2 ℃
в 12 часов - 3 ℃
в 15 часов – 6 ℃
в 18 часов – 4 ℃
в 21час – 0 ℃.
Слайд 4
Вы пришли в магазин купить конфеты.
Пусть
их цена 150 рублей за 1 кг.
Сколько
денег вы отдадите за 1кг, за 2кг, за 3кг, за 4кг, за 5кг?
Слайд 5
Классная работа.
Способы задания функции
Цель урока:
познакомиться
со способами задания функции; научиться определять способы задания функции;
находить значение аргумента и значение функции, заданной формулой.06.03.2020
Слайд 6 Функция считается заданной, если указаны её область определения
и правило, с помощью которого можно по каждому значению
независимой переменной найти значение зависимой переменной.
Слайд 7
Описательный способ задания функции.
Каждому однозначному натуральному числу поставили
в соответствие число вдвое большее.
Область определения некоторой функции –
двузначные натуральные числа, большие 10,но меньшие 20, а значения функции
на 5 меньше соответствующего значения аргумента.
Температура воздуха в течение суток
меняется в зависимости от времени, в 6 часов-0 ℃, в 9 часов-2 ℃, в 12 часов-3 ℃, в 15 часов-6 ℃, в 18 часов-4 ℃, в 21час-0 ℃.
Вы пришли в магазин купить конфеты. Пусть их цена 150 рублей за 1кг.
Сколько денег вы отдадите
за 1кг, за 2кг, за 3кг, за 4кг, за 5кг?
Слайд 8
Способ задания функции с помощью формулы.
Функция задана формулой
У=2Х
Функция задана формулой
У=Х-5
С=150К
Слайд 10
Физкультминутка
Сколько?
Сколько функций на картинках, столько приседаем.
Сколько здесь табличек?
Ручки поднимаем.
Посчитаем сколько формул, столько наклонимся.
Влево, вправо, влево.
А теперь
садимся.
Слайд 11
Числа Фибоначчи
0, 1, 1, 2, 3, 5, 8,
13, 21, 34, 55, 89, 144, 233, 377, 610,
987и так далее
В одном из своих самых известных трудов под названием «Liber abaci», Леонардо Пизанский приводит уникальную закономерность чисел. Леонардо Пизанский получил свое знаменитое прозвище «Фибоначчи».
Из-за своего повсеместного применения в природе, золотое сечение (именно так число Фибоначчи иногда называют в искусстве и математике) считается одним из самых гармонизирующих законов мироздания, который упорядочивает структуру окружающего нас мира и направляет жизнь на развитие. Так, правило золотого сечения применяется природой. Вот некоторые примеры.
Слайд 14
Ответим вместе!
Какую цель в начале урока мы
поставили?
Достигли поставленную цель?
Чему новому мы сегодня научились?
Какие
трудности встретили?
Слайд 15
Оцени себя
На уроке мне было всё понятно. Я
со всем справился самостоятельно!
На уроке мне почти всё было
понятно. Не всё получалось сразу, но я всё равно справился с заданиями!Мне многое непонятно! Мне требуется помощь!
Слайд 16
Домашнее задание
Обязательная часть: параграф 21, вопросы 1, 2.
Упражнения 791, 796.
Дополнительная часть: Упражнения 794, 798.
Творческое задание: Сообщение
по темам на выбор: - Кто такой Фибоначчи?
- Золотое сечение.
- Использование функции вокруг нас.





























