Презентация на тему Федерация водного поло Росссии

привлечь внимание к возможности изучения многих ситуаций в спорте

с математических позиций, и к целесообразности более обоснованных количественных и качественных оценок спортивных явлений.

Методы исследования: сравнительный анализ и моделирование.

обеспечивающее наибольший эффект в игре.
2. Составление для спортсменов диеты,

удовлетворяющей требованиям медиков и, в то же время, наиболее экономной и сохраняющей вес спортсмена в определенных рамках.
3. Распределение между игроками команды обязанностей таким способом, чтобы общая результативность действий всей команды оказалась наибольшей.
4. Какое значение имеют броски в современном водном поло.

в организации тренировок и соревнований,
в комплектовании спортивных команд,

в распределении обязанностей игроков команды,
в выборе тактики игры и т. п.

решений могут оказаться столь значительными, что предварительный количественный и

качественный анализ становится обязательным.
В этих случаях не обойтись без применения научных, в первую очередь математических, методов..

игроков.
Перед новым тренером стоит задача:
Распределить между игроками команды обязанности

так, чтобы результативность команды оказалась наибольшей.

1 5 2
2 6

4 1 2 4
2 2 3 6 2 4
3 1 5 4 2 5
1 3 3 1 2 6
2 5 4 2 6 2

Ф(Р) = 6+6+6+5+6+6=35
1 0 0 0 0 0
0 1 0 0 0 0
0 0 0 1 0 0
0 0 1 0 0 0
0 0 0 0 0 1
0 0 0 0 1 0

h0- высота с которой бросают мяч;
L – расстояние от

бросающего до ворот;
g – ускорение свободного падения;
υ0 – начальная скорость;
υ 0х – проекция начальной скорости на оси Х;
υ 0y – проекция начальной скорости на оси Y;
α – угол броска над поверхностью воды;
h=1,5м – высота от поверхности воды до ворот.

Y:

поверхностью воды.

0:

L=x= υ0tcosα=υ0cosα(υ0sinα+√ υ0²sin²α-2g(1,5- h0))/g=

(υ0²sinαcosα+υ0cosα√υ0²sin²α-2g(1,5- h0))/g;

При h0=1,5 ;

L= (υ0²sin2α)/g;
Теперь найдем L из t2 , где sinα < 0:

L=(υ0²sinαcosα+υ0cosα√υ0²sin²α-2g(1,5-h0))/g;

При h0=1,5; L= (υ0²sin2α)/g.

м
L = 5 м




1) α=-15
5 = (υ0²sin30)/9,8
υ0=7 √2 м/с

2)

α=45
5 = (υ0²sin90)/9,8
υ0=7м/с

Вывод: чем меньше угол броска, тем больше начальная скорость(т.е. сильнее бросок).

всех видах продуктов составят сумму :
Запасы питательных веществ

β1 , β2 , …. , βn
Различные продукты
Z1, Z2 . . .., Zn ;
a ij запасы (в некоторых единицах) питательного вещества вида βj в продукте Zij;
стоимость некоторой единицы продукта С;
минимальная норма питательного вещества bi ;
количество продукта Xj;

a i1 X1 + ... + a j1 Xj + ... + ainXm.

a ijX1 + ... + a i j Xj + ... + ainXm. ≥ bi
i = 1, ... , m (1)

Общая стоимость приобретенных продуктов составит:

F(X)= C1 * X1 +C 2 * X2 + ...+ Cn * Xn

(т = 5) и два типа продуктов (n =

2).

Условия неотрицательности переменных и минимизируемая форма примут вид:

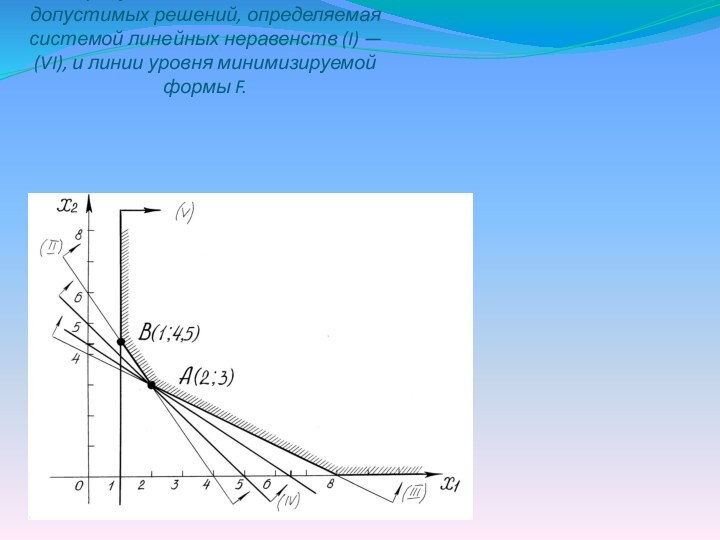
2X1 + 3х2 ≥ 13, (I)
Зх1 + 2х2 ≥12, (II)
2х1 + 4х2 ≥16, (III)
2х1 + 2х2 ≥ 10, (IV)
x1 ≥ 1, (V)
х2 > 0, (VI)
F(X) = 2xl + 3х2