Презентация на тему Концепция современного естествознания

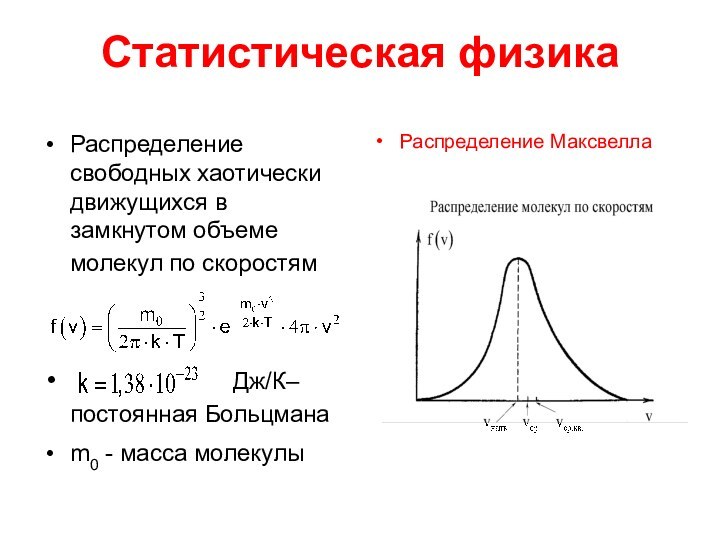
Жан-Батист Жозеф Фурье : поток тепла пропорционален градиенту температуры:


Q

– количество тепла, проходящего через некоторую поверхность S в единицу времени (количество энергии, передаваемой путем теплопередачи);
dT/dx – быстрота изменения температуры вдоль оси ОХ (величина градиента температуры),
σ – коэффициент теплопроводности.
Знак “–“ перед правой частью указывает на то, что тепло распространяется в сторону уменьшения температуры (необратимый процесс установления равновесия).

не имеющая внутренней структуры. Состояние макросистемы характеризуется некоторым количеством

величин – параметров. Эти величины характеризуют всю систему в целом, в разных точках среды могут иметь различные значения и изменяться с течением времени (неравновесное состояние).
Равновесным называется такое состояние, при котором в изолированной системе при отсутствии внешних воздействий все параметры системы приобретают постоянные значения.
В термодинамике вместо классического движения рассматривается переход из одного равновесного состояния в другое равновесное состояние.

Европе потребовала изучения закономерностей превращения теплоты в механическую работу

в тепловых двигателях. Пионерские исследования, заложившие основы термодинамики:
французский инженер и физик Сади Карно (1796-1832),
немецкий физик-теоретик Рудольф Клаузиус (1822-1888)
австрийский физик-теоретик Людвиг Больцман (1844-1906).
Первые положения термодинамики были изложены в сочинении Сади Карно «О движущей силе огня и о машинах, способных развивать эту силу» (1824 г). Первоначальная задача сводилась к исследованию условий, при которых превращение теплоты в работу является наиболее оптимальным.

различных видов энергии, теплоты и работы.
Первое начало устанавливает

количественные соотношения, имеющие место при превращениях энергии из одних видов в другие.
Первое начало термодинамики (закон сохранения энергии):

количество тепла, сообщенное системе, идет на приращение внутренней энергии системы и на совершение работы над внешними телами;
невозможен вечный двигатель первого рода, т.е. такой периодически действующий двигатель, который совершал бы работу в большем количестве, чем получал извне энергию.

превращения, то есть определяет возможные направления процессов.
Второе начало термодинамики:
невозможны

такие процессы, единственным конечным результатом которых был бы переход тепла от тела, менее нагретого, к телу, более нагретому;
невозможен вечный двигатель второго рода, т.е. такой периодически действующий двигатель, который получал бы тепло от одного резервуара и превращал это тепло полностью в работу.

которого:
размерами молекул можно пренебречь;
силами межмолекулярного взаимодействия можно пренебречь (на

расстоянии молекулы друг с другом не взаимодействуют);
друг с другом и со стенками сосуда молекулы взаимодействуют по законам абсолютно упругого удара.
Состояние идеального газа описывается уравнением Менделеева-Клайперона

молекул. При столкновениях выполняется закон сохранения энергии движения. Между

столкновениями молекулы движутся свободно, т.е. по прямым линиям с постоянной скоростью;
– средние кинетические энергии молекул разных газов, находящихся при одинаковой температуре равны между собой.
– средняя скорость молекул пропорциональна корню квадратному из абсолютной температуры;

молекул по скоростям

Дж/К– постоянная Больцмана
m0 - масса молекулы

Распределение Максвелла

скорости каждой отдельной частицы находится в единичном интервале скоростей

около скорости .
вероятность того, что скорость
любой частицы ансамбля принимает какое-либо значение в интервале от нуля до бесконечности, равна единице.
Зная f(v), можно вычислить число частиц , модули скоростей которых лежат в интервале значений от v1 до v2.

значение скорости, однако при этом конкретному состоянию ансамбля частиц

соответствуют вполне определенные значения скоростей и энергии:
Средняя скорость
Среднеквадратичная
скорость

Средняя кинетическая
энергия

изолированной системе частиц, находящейся в состоянии теплового равновесия, динамическое

состояние каждой отдельной молекулы непрерывно изменяется, а макросостояние системы в целом остается стационарным, т.е. характеризуется постоянными значениями температуры и давления.
Классическая статистическая механика (Больцман) позволяет предсказывать свойства систем на основе анализа статистического поведения частиц, из которых они состоят.

вероятностью понимается предел, к которому стремиться относительная частота появления

некоторого события при достаточно большом числе повторений опыта при неизменных внешних условиях.

последующего развития естествознания (неклассического)
– введение вероятности в физике,

как объясняющего принципа, а не как аппроксимации;
– использование вероятностей и статистического подхода к исследованию микросостояний сложных систем для предсказания макроскопических свойств.

способами, каждому из которых соответствует некоторое микросостояние.
Число различных микросостояний,

соответствующих данному макросостоянию, называется статистическим весом, или термодинамической вероятностью.

двумя половинками сосуда; способов 24=16

макросостояния равна отношению его статистического веса к полному числу

состояний.
Отметим, что Ω не обладает свойство аддитивности. Если система, к примеру, состоит из двух подсистем, то Ω=Ω1 Ω2. Поэтому в качестве характеристики вероятности состояния принимается величина
S=k lnΩ,
которая называется энтропией.

Энтропия изолированной системы возрастает, т.к. система переходит из менее

вероятных в более вероятные состояния;
Энтропия системы, находящейся в равновесном состоянии, максимальна.

Стругацких: Демон Максвелла -- важный элемент мысленного эксперимента крупного

английского физика Максвелла. Предназначался для нападения на второй принцип термодинамики. В мысленном эксперименте Максвелла демон располагался рядом с отверстием в переборке, разделяющей сосуд, наполненный движущимися молекулами. Работа демона состоит в том, чтобы выпускать из одной половины сосуда в другую быстрые молекулы и закрывать отверстия перед носом медленных. Идеальный демон способен таким образом без затраты труда создать очень высокую температуру в одной половине сосуда и очень низкую -- в другой, осуществляя вечный двигатель второго рода.

упорядоченным.
Энтропия является мерой молекулярного беспорядка в системе. Тепловое

движение приводит к увеличению степени беспорядка в системе (увеличению энтропии).
Сообщение системе тепла приводит к усилению теплового движения и увеличению энтропии.