- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Автомат Мура
Содержание
- 2. Эдвард Форест Мур(23 ноября 1925 – 14 июня 2003)Американский профессор математики и информатики
- 3. Классификация детерминированных автоматов
- 4. Модель автомата
- 5. Модель МураАвтомат Мура функционирует в соответствии с
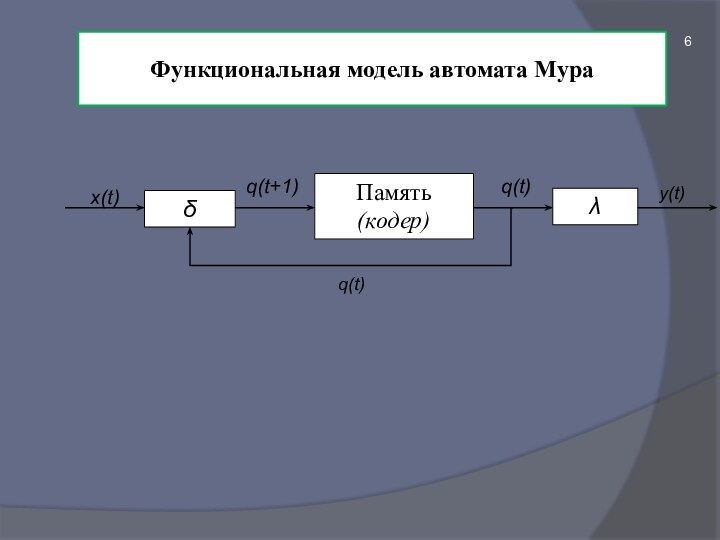
- 6. Функциональная модель автомата Мураq(t+1)q(t)x(t)y(t)q(t)
- 7. КС – комбинаторная схема (микропрограммные модули);R –
- 8. Формальное описаниеM= (3);Z = {z0,z1,…, zn}
- 9. Табличный метод задания автоматовАвтомат Мура:Анализ данного автомата:Каждому
- 10. Отмеченная таблица переходов автомата МураГрафовый методA= {a0,z1,…, zi}A = Z – множество состояний конечного автомата.
- 11. Матричный методВыходные сигналы задаются в виде вектора
- 12. Матрица соединений автомата МураЭлемент cij равен множеству
- 13. Скачать презентацию
- 14. Похожие презентации
Эдвард Форест Мур(23 ноября 1925 – 14 июня 2003)Американский профессор математики и информатики












Слайд 5
Модель Мура
Автомат Мура функционирует в соответствии с законами:
q(t+1)
= δ(q(t), x(t)) (1);
y(t) = λ(q(t))
(2), гдеq(t) – множество состояний в момент времени t;
t – текущий момент времени;
t+1 – следующий момент времени;
q(t+1) – состояние автомата в следующий момент времени;
x(t) – множество входных сигналов;
y(t) – множество выходных сигналов;
δ – функция переходов;
λ – функция выходов.
Слайд 7
КС – комбинаторная схема (микропрограммные модули);
R – регистр
состояний;
DC – дешифратор;
U – вспомогательные сигналы (переменные);
V – множество
двоичных кодов;a=q(t) – состояние автомата;
С – синхросигналы;
X – входной сигнал;
Y – выходной сигнал.
Структурная модель автомата Мура
Слайд 8
Формальное описание
M=
(3);
Z = {z0,z1,…, zn} (4);
X = {x0,x1,…,
xm} (5);Y = {y0,y1,…, yQ} (6);
(z(t), x(t))= z(t+i) (7), где i=1,..n;
(x(t)) = y(t) (8), где
M - автомат Мура (кортеж из 6 – и элементов),
Z – алфавит состояний,
- функция переходов,
- функция выходов.