- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Военная топография
Содержание
- 2. Содержание: Введение 1 Измерение расстояний и площадей
- 3. Военная топография – это специальная воинская дисциплина о способах
- 4. 1.1 Численный масштаб Степень уменьшения линий на карте
- 5. Расстояние на местности в метрах или километрах,
- 6. 1.2 Линейный масштаб Измерения по линейному масштабу производятся
- 7. 1.3 Измерение длинных и извилистых линий Измерение длинных
- 8. Для измерения извилистой ломаной линии шаг циркуля
- 9. 1.4 Измерение расстояний с помощью курвиметра Курвиметр. Для
- 10. Для измерения расстояния следует предварительно вращением колесика
- 11. 1.5 Способы измерения площадей по карте1. Приближенную
- 12. 2.1 Географические координаты Широты отсчитываются по дуге
- 13. 2.2 Определение географических координат и нанесение на
- 14. 2.3 Плоские прямоугольные координаты Плоскими прямоугольными координатами называются
- 15. 2.4 Использование координатной сетки при работе с
- 16. 2.5 Определение прямоугольных координат точек. Нанесение на
- 17. Скачать презентацию
- 18. Похожие презентации











Слайд 3 Военная топография – это специальная воинская дисциплина о способах и
средствах изучения и оценки местности, ориентирования на ней и
производства полевых измерений для обеспечения боевой деятельности войск .Главной задачей военной топографии является изыскание наиболее рациональных способов и средств получения информации о местности. Изучая эту дисциплину, военнослужащие, готовясь к практическим действиям в бою, развивают в себе наблюдательность, точность, умение анализировать результаты наблюдения и делать выводы о влиянии местности на выполнение боевой задачи.
Топографические карты широко используются командирами и штабами всех степеней для решения разнообразных задач, связанных с действиями войск на местности. По карте изучают и оценивают местность, ориентируются на местности, определяют координаты позиций и целей, выполняют различные инженерно-технические расчеты.
ВВЕДЕНИЕ
Слайд 4
1.1 Численный масштаб
Степень уменьшения линий на карте относительно
горизонтальных проложений соответствующих им линий на местности называется масштабом
карты (плана). Иначе говоря, под масштабом разумеют отношение длины линии на карте к длине горизонтального проложения соответствующей ей линии на местности.Это числовое выражение называют численным масштабом и представляют в виде отношения единицы к числу, показывающему, во сколько раз уменьшены длины линий местности при изображении их на карте. Например, масштаб 1:50 000 показывает, что все линейные размеры на карте уменьшены в 50 000 раз, т. е. 1 см карты на местности соответствует 500 м, или 0,5 км.
Рис. 1. Оформление численного и линейного масштабов на топографических картах и планах городов
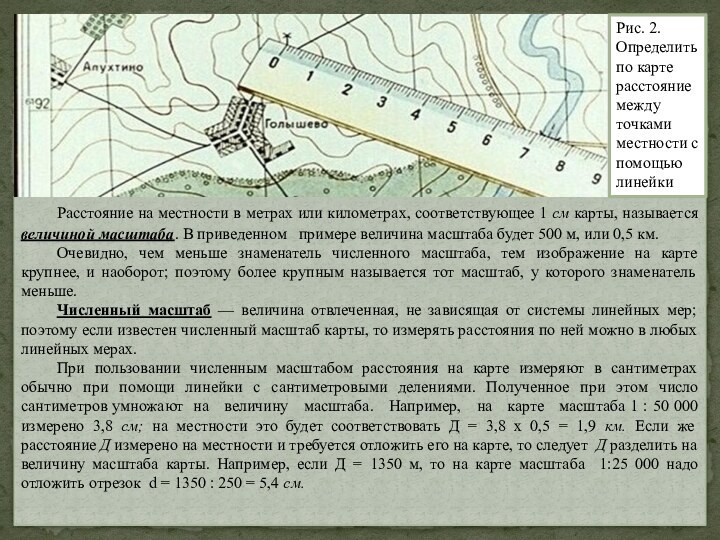
Слайд 5 Расстояние на местности в метрах или километрах, соответствующее
1 см карты, называется величиной масштаба. В приведенном
примере величина масштаба будет 500 м, или 0,5 км.Очевидно, чем меньше знаменатель численного масштаба, тем изображение на карте крупнее, и наоборот; поэтому более крупным называется тот масштаб, у которого знаменатель меньше.
Численный масштаб — величина отвлеченная, не зависящая от системы линейных мер; поэтому если известен численный масштаб карты, то измерять расстояния по ней можно в любых линейных мерах.
При пользовании численным масштабом расстояния на карте измеряют в сантиметрах обычно при помощи линейки с сантиметровыми делениями. Полученное при этом число сантиметров умножают на величину масштаба. Например, на карте масштаба 1 : 50 000 измерено 3,8 см; на местности это будет соответствовать Д = 3,8 х 0,5 = 1,9 км. Если же расстояние Д измерено на местности и требуется отложить его на карте, то следует Д разделить на величину масштаба карты. Например, если Д = 1350 м, то на карте масштаба 1:25 000 надо отложить отрезок d = 1350 : 250 = 5,4 см.
Рис. 2. Определить по карте расстояние между точками местности с помощью линейки
Слайд 6
1.2 Линейный масштаб
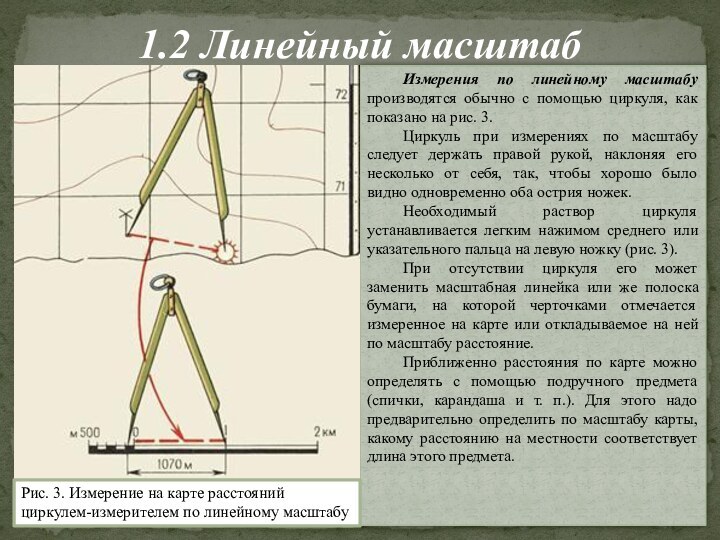
Измерения по линейному масштабу производятся обычно
с помощью циркуля, как показано на рис. 3.
Циркуль при
измерениях по масштабу следует держать правой рукой, наклоняя его несколько от себя, так, чтобы хорошо было видно одновременно оба острия ножек. Необходимый раствор циркуля устанавливается легким нажимом среднего или указательного пальца на левую ножку (рис. 3).
При отсутствии циркуля его может заменить масштабная линейка или же полоска бумаги, на которой черточками отмечается измеренное на карте или откладываемое на ней по масштабу расстояние.
Приближенно расстояния по карте можно определять с помощью подручного предмета (спички, карандаша и т. п.). Для этого надо предварительно определить по масштабу карты, какому расстоянию на местности соответствует длина этого предмета.
Рис. 3. Измерение на карте расстояний циркулем-измерителем по линейному масштабу
Слайд 7
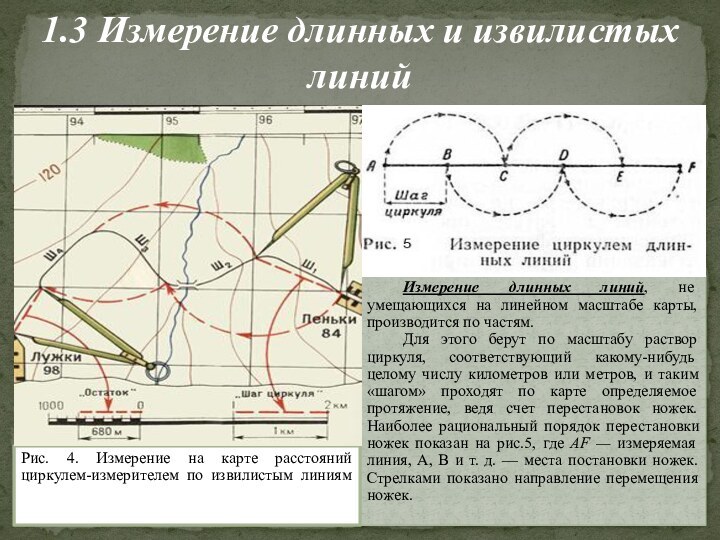
1.3 Измерение длинных и извилистых линий
Измерение длинных линий,
не умещающихся на линейном масштабе карты, производится по частям.
Для этого берут по масштабу раствор циркуля, соответствующий какому-нибудь целому числу километров или метров, и таким «шагом» проходят по карте определяемое протяжение, ведя счет перестановок ножек. Наиболее рациональный порядок перестановки ножек показан на рис.5, где AF — измеряемая линия, А, В и т. д. — места постановки ножек. Стрелками показано направление перемещения ножек.
Рис. 4. Измерение на карте расстояний циркулем-измерителем по извилистым линиям
Слайд 8 Для измерения извилистой ломаной линии шаг циркуля берется
меньше (например, 0,5 см или 1 см), сообразно длине
звеньев линии. Но более удобно измерение вести следующим образом (рис. 6).Пусть требуется измерить по карте расстояние по линии ABCDEF. Установив раствор циркуля по первому звену линии, т. е. по АВ, переставляем заднюю ножку в точку А1 (на продолжении следующего по ходу измерения звена ВС). Оставляя ее теперь на месте, т. е. в точке А1 увеличиваем раствор циркуля перемещением передней его ножки в точку С. Затем, не изменяя положения передней ножки, заднюю из точки А1 переставляем в точку А2 (на продолжении третьего звена CD). После этого переднюю ножку перемещаем дальше в точку D и т. д., пока не пройдем, таким образом, всю линию.
В итоге получим отрезок A4F, равный искомой длине линии на карте. Остается, не изменяя полученного раствора циркуля, перенести его на линейный масштаб или миллиметровую линейку и определить расстояние, как было указано выше.
Слайд 9
1.4 Измерение расстояний с помощью курвиметра
Курвиметр. Для определения
расстояний по карте очень удобен, особенно при измерениях длинных
кривых и извилистых линий, специальный прибор, называемый курвиметром (рис. 7).Внизу прибора имеется колесико, соединенное системой передач со стрелкой. При движении колесика вдоль измеряемой по карте линии стрелка передвигается по циферблату и указывает пройденное колесиком расстояние.
Деления на шкале циферблата бывают различные: на одних курвиметрах они обозначают путь, проходимый колесиком, в сантиметрах, на других же — непосредственно расстояния на местности в зависимости от масштаба карты. Так, на рис.7 показан курвиметр с тремя шкалами, из которых каждая соответствует определенному масштабу карты
(1 : 25000, 1 : 50 000 и 1 : 100 000).
На рис. 7 стрелка курвиметра показывает по шкале:
для масштаба 1:25 000 — 4,2 км,
для масштаба 1 : 50 000 — 8,5 км
для масштаба 1 : 100 000 — 17 км.
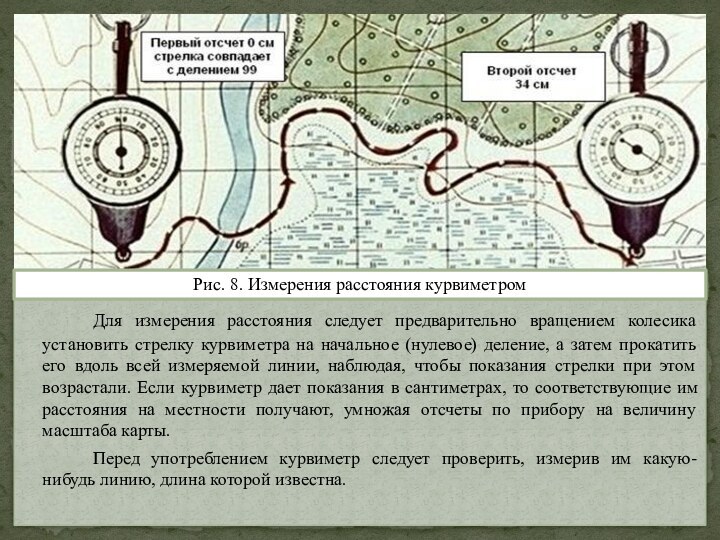
Слайд 10 Для измерения расстояния следует предварительно вращением колесика установить
стрелку курвиметра на начальное (нулевое) деление, а затем прокатить
его вдоль всей измеряемой линии, наблюдая, чтобы показания стрелки при этом возрастали. Если курвиметр дает показания в сантиметрах, то соответствующие им расстояния на местности получают, умножая отсчеты по прибору на величину масштаба карты.Перед употреблением курвиметр следует проверить, измерив им какую-нибудь линию, длина которой известна.
Рис. 8. Измерения расстояния курвиметром
Слайд 11
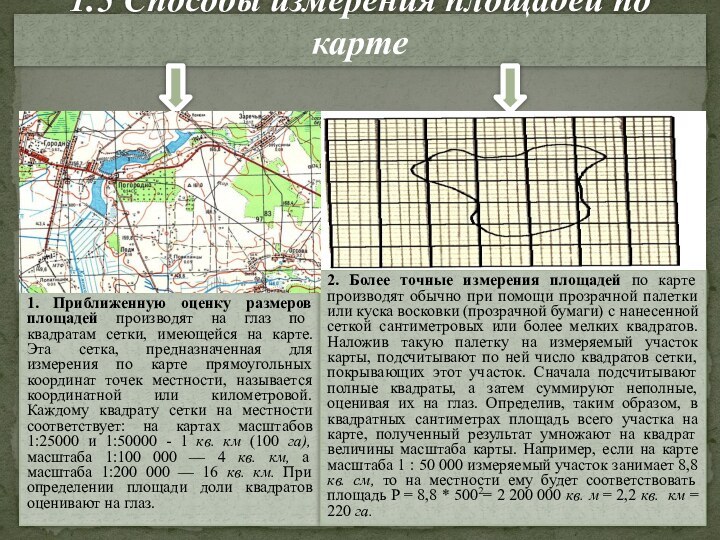
1.5 Способы измерения площадей по карте
1. Приближенную оценку
размеров площадей производят на глаз по квадратам сетки, имеющейся
на карте. Эта сетка, предназначенная для измерения по карте прямоугольных координат точек местности, называется координатной или километровой. Каждому квадрату сетки на местности соответствует: на картах масштабов 1:25000 и 1:50000 - 1 кв. км (100 га), масштаба 1:100 000 — 4 кв. км, а масштаба 1:200 000 — 16 кв. км. При определении площади доли квадратов оценивают на глаз.2. Более точные измерения площадей по карте производят обычно при помощи прозрачной палетки или куска восковки (прозрачной бумаги) с нанесенной сеткой сантиметровых или более мелких квадратов. Наложив такую палетку на измеряемый участок карты, подсчитывают по ней число квадратов сетки, покрывающих этот участок. Сначала подсчитывают полные квадраты, а затем суммируют неполные, оценивая их на глаз. Определив, таким образом, в квадратных сантиметрах площадь всего участка на карте, полученный результат умножают на квадрат величины масштаба карты. Например, если на карте масштаба 1 : 50 000 измеряемый участок занимает 8,8 кв. см, то на местности ему будет соответствовать площадь Р = 8,8 * 5002= 2 200 000 кв. м = 2,2 кв. км = 220 га.
Слайд 12
2.1 Географические координаты
Широты отсчитываются по дуге меридиана
в обе стороны от экватора, начиная с 0° до
90°.В северном полушарии широты считаются северными, а в южном — южными.
Все точки, лежащие на одной географической параллели, имеют одинаковую широту, поэтому одна широта еще не определяет положения точки на земной поверхности. Необходимо знать вторую координату — долготу.
Угол OCN (рис. 9) будет долготой точки М. Как уже указывалось, у нас за начальный принят Гринвичский меридиан.
Долготы отсчитываются по дуге экватора или параллели в обе стороны от начального меридиана, начиная с 0° до 180°. Все точки, лежащие на одном меридиане, имеют одинаковую долготу.
Разность долгот двух пунктов показывает не только их взаимное расположение, но и разницу во времени в этих пунктах в один и тот же момент: каждые 15° по долготе соответствуют одному часу времени. Например, долгота г. Москва 37°37' (восточная), а г. Хабаровск 135°05', т. е. последний лежит восточнее на 97°28'. Таким образом, когда в Москве полдень (13 часов), в Хабаровске 19 часов 30 минут (по поясному времени 20 часов).
Рис. 9. Система географических координат на земной поверхности
Географическими координатами называются угловые величины — широта и долгота, определяющие положение точек на земном шаре.
Очевидно, что для любой точки М на поверхности шара (рис. 9) угол MCN будет широтой этой точки.
Слайд 13 2.2 Определение географических координат и нанесение на карту
объектов по известным координатам
Пользуясь минутной рамкой карты можно:
1. Определить
географические координаты любой точки на карте.
Например, координаты точки А (рис.10). Для этого необходимо с помощью циркуля-измерителя измерить кратчайшее расстояние от точки А до южной рамки карты, затем приложить измеритель к западной рамке и определить количество минут и секунд в измеренном отрезке, сложить полученное (измеренное) значение минут и секунд (0'27") с широтой юго-западного угла рамки - 54°30'.
Широта точки на карте будет равна: 54°30'+0'27" = 54°30'27".
Долгота определяется аналогично.
Измеряют с помощью циркуля-измерителя кратчайшее расстояние от точки А до западной рамки карты, прикладывают циркуль-измеритель к южной рамке, определяют количество минут и секунд в измеренном отрезке (2'35") складывают полученное (измеренное) значение с долготой юго-западного угла рамки- 45°00'.
Долгота точки на карте будет равна: 45°00'+2'35" = 45°02'35"
2. Нанести любую точку на карту по заданным географическим координатам.
Например, точку Б широта: 54°31 '08", долгота 45°01 '41".
Для нанесения на карту точки по долготе необходимо провести истинный меридиан через данную точку, для чего соединить одинаковое количество минут по северной и южной рамке; для нанесения на карту точки по широте необходимо провести параллель через данную точку, для чего соединить одинаковое количество минут по западной и восточной рамке. Пересечение двух прямых определит местоположение точки Б.Рис. 10. Определение географических координат точки по карте (точка А)
и нанесение на карту точки по географическим координатам (точка Б)
Географические координаты точки, расположенной на карте, определяют от ближайших к ней параллели и меридиана, широта и долгота которых известна.
Рамка топографической карты разбита на минуты, которые разделены точками на деления по 10 секунд в каждом. На боковых сторонах рамки обозначены широты, а на северной и южной - долготы.
Слайд 14
2.3 Плоские прямоугольные координаты
Плоскими прямоугольными координатами называются линейные
величины — абсцисса и ордината, определяющие положение точек на
плоскости.Две взаимно перпендикулярные прямые X и У, относительно которых определяется положение точек (рис. 11), называются осями координат; из них ось X называется осью абсцисс, а ось Y — осью ординат. Точка пересечения осей — точка О — называется началом координат.
Оси координат делят плоскость на четыре четверти, счет которых ведется в топографии по ходу часовой стрелки от положительного направления оси X. За положительное направление осей координат принимается для оси абсцисс (X) направление на север, а для оси ординат (У) — на восток.
Положение любой точки М на плоскости относительно начала координат О (рис. 11) определяется кратчайшими расстояниями до нее от осей координат, измеренными в каких-либо мерах длины, например в метрах. Эти расстояния, являющиеся координатами точек, изобразятся, очевидно, отрезками прямых линий, перпендикулярных к одной из координатных осей и параллельных другой.
Координата X — абсцисса — вверх от оси У считается положительной, а вниз от нее — отрицательной.
Координата Y — ордината — вправо от оси X считается положительной, а влево от нее — отрицательной.
Таким образом, точки на рис. 11 будут иметь следующие координаты:
М1... x1 = +2 м; y1 = +4 м
M2... x2 = - 4 м; у2 = +6 м
M3... x3 = - 2 м; у3 = - 4 м
M4... x4 = +6 м; у4 = - 6 м
Слайд 15
2.4 Использование координатной сетки при работе с картой
Все
топографические карты, за исключением карт масштаба 1:1000000, составляются в
единой равноугольной проекции — раздельно по 6-градусным зонам. Это позволяет каждую такую зону уровенной поверхности развертывать в плоскость, т. е. изображать на карте без практически заметных искажений, вызываемых кривизной Земли.Координатная сетка весьма широко используется при работе с картой. Основное ее назначение — облегчить и упростить определение прямоугольных координат точек местности при целеуказании по карте.
Вместе с тем она облегчает ориентирование на карте и указание на ней местоположения различных объектов при докладах, постановке задач, передаче распоряжений и составлении донесений.
Наконец, она помогает быстро оценивать по карте на глаз расстояния и определять азимуты направлений.
Рис. 12. Система плоских прямоугольных координат на картах. Координатная сетка (справа)
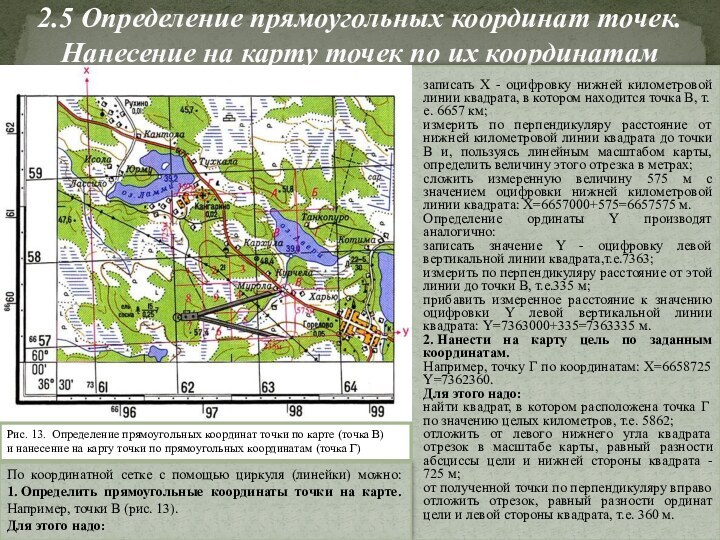
Слайд 16 2.5 Определение прямоугольных координат точек. Нанесение на карту
точек по их координатам
записать X - оцифровку нижней километровой
линии квадрата, в котором находится точка В, т.е. 6657 км;измерить по перпендикуляру расстояние от нижней километровой линии квадрата до точки В и, пользуясь линейным масштабом карты, определить величину этого отрезка в метрах;
сложить измеренную величину 575 м с значением оцифровки нижней километровой линии квадрата: X=6657000+575=6657575 м.
Определение ординаты Y производят аналогично:
записать значение Y - оцифровку левой вертикальной линии квадрата,т.е.7363;
измерить по перпендикуляру расстояние от этой линии до точки В, т.е.335 м;
прибавить измеренное расстояние к значению оцифровки Y левой вертикальной линии квадрата: Y=7363000+335=7363335 м.
2. Нанести на карту цель по заданным координатам. Например, точку Г по координатам: Х=6658725 Y=7362360. Для этого надо:
найти квадрат, в котором расположена точка Г по значению целых километров, т.е. 5862;
отложить от левого нижнего угла квадрата отрезок в масштабе карты, равный разности абсциссы цели и нижней стороны квадрата - 725 м;
от полученной точки по перпендикуляру вправо отложить отрезок, равный разности ординат цели и левой стороны квадрата, т.е. 360 м.
По координатной сетке с помощью циркуля (линейки) можно:
1. Определить прямоугольные координаты точки на карте.
Например, точки В (рис. 13).
Для этого надо:
Рис. 13. Определение прямоугольных координат точки по карте (точка В)
и нанесение на карту точки по прямоугольных координатам (точка Г)





























