Слайд 2
Объект управления-авто
Скорость
движения
Расстояние
до обочины
Расстояние
до препятствия
Слайд 3
Ситуация
Ситуация-набор значений признаков, описывающих состояние объекта управления в
некоторый момент времени
Пусть задано 3 признака:
Скорость движения 0-120 км/ч,
Расстояние до обочины 0-10 м,
Расстояние до препятствия 0-500 м,
Общее число ситуаций – 24*10*10
Слайд 4
Описание типовых ситуаций
до препятствия,T3,D3>
T1={большая,средняя,малая}
T2={большое,небольшое,среднее,малое}
T3={большое,среднее,малое}
D1={0,5,…,120} D2={0,1,…,10} D3={0,50,…,500}
Общее число ситуаций – 3*4*3
Слайд 5
Учет дополнительных особенностей
Пусть также необходимо учитывать состояние дороги
Тогда
степень частоты, при котором принимается решение
увеличить скорость:
«очень часто»
- 1
«часто» - 0,8
«редко» - 0,3
Значение признака «скорость движения» при котором принимается решение увеличить скорость:
{<0,3/малая>, <0,8/средняя>, <1/большая>}
Слайд 6
Формальное определение ситуации
Слайд 7
Пример нечеткой ситуации
{,
, }/Расстояние до обочины>,
}
Слайд 8
Подходы к построению нечеткой ситуационной сети
Прямой подход –
заключается в моделировании переходов системы из одной нечеткой ситуации
в другую. Для этого предварительно выявляется множество управляющих решений R=(R1,R2,…Rf). Эти управляющие решения задаются в виде нечетких отношений определенного типа между термами признаков.
Обратный подход – заключается в том, что на множестве эталонных нечетких ситуаций задается некоторое отношение, граф которого отражает возможные переходы из ситуации в ситуацию. И нечеткая ситуационная сеть формируется посредством задания необходимых для этих переходов управляющих решений и степеней предпочтения.
Слайд 9
Пример построения НСС с помощью прямого подхода
Пусть признак
некоторого объекта управления имеет терм – множество {«малое», «среднее»,
«большое»}. Лингвистические переменные имеют терм – множества {«немного», «сильно»}, {«немного», «сильно»}, {«не изменять»} соответственно.
Слайд 11
Воздействие управляющего решения на признак
Слайд 12
Воздействие управляющего решения на признак(пример)
Пусть признак некоторого объекта
управления, из предыдущего примера, имеет следующее нечеткое значение:
Слайд 13
Воздействие управляющего решения на признак(пример)
Слайд 14
Построение НСС с помощью прямого подхода(алгоритм)
Слайд 15
Построение НСС с помощью прямого подхода(алгоритм)
Слайд 16
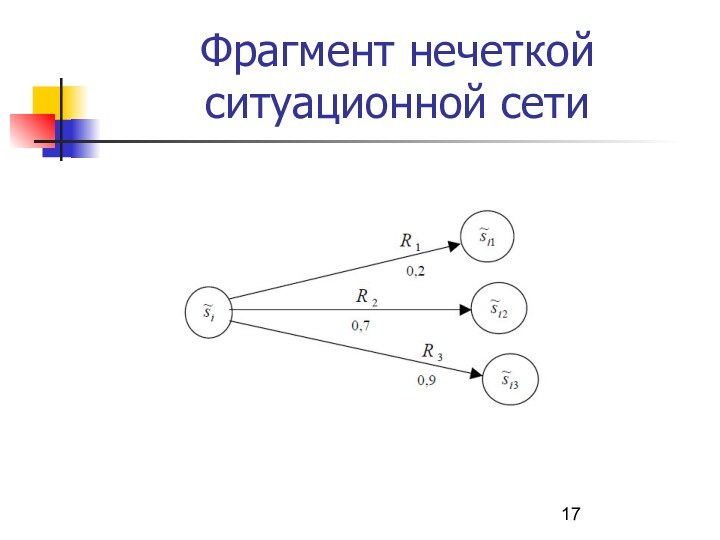
Взаимосвязь управляющих решений
Иногда возникает ситуация, что применение одного
управляющего решения по отдельному признаку может вызвать изменение значений
других признаков, что в конечном итоге соответствует применению управляющих решений по этим признакам.
Слайд 17
Фрагмент нечеткой ситуационной сети
Слайд 18
Модель ситуация-действие
Управляющее решение, которое необходимо применять при входной
ситуации s0 определяется ситуацией, в некотором смысле наиболее близкой
ситуации s0.
Меры близости:
Нечеткая общность ситуаций
Нечеткое равенство ситуаций
Нечеткое включение ситуаций
Слайд 19
Модель ситуация-стратегия управления-действие
Модель отличается от предыдущей отсутствием явного
описания продукций, на основе которых осуществляется вывод управляющих решений.
Модель содержит набор эталонных нечетких ситуаций, описывающих возможные состояния объекта управления. Управляющие решения, соответствующие текущим нечетким ситуациям, формируются на основе анализа возможных переходов между текущей ситуацией и целевой, т.е. ситуацией, в которую желательно перевести объект управления
Слайд 20
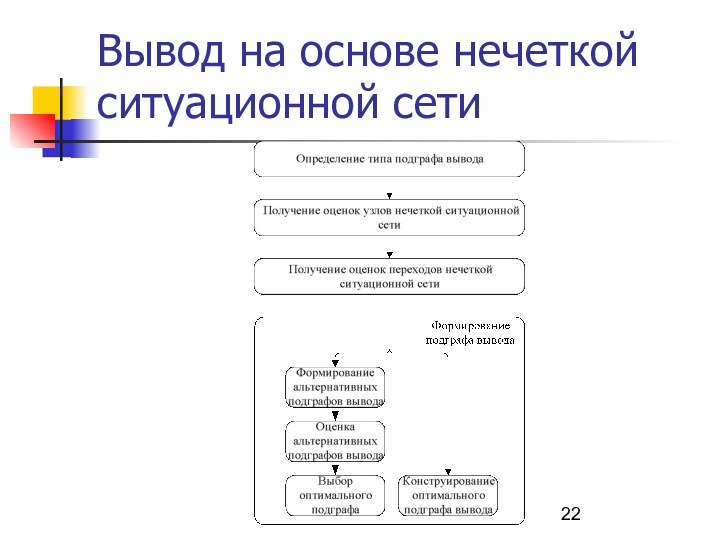
Вывод на основе нечеткой ситуационной сети
Ситуационная сеть может
быть представлена в виде ориентированного графа G=(W,A), где W
– множество узлов – состояний, A – множество дуг-переходов между состояниями.
Метод вывода по нечёткой ситуационной сети основывается
на трактовке в виде задачи поиска некоторого связного
подграфа, содержащего некоторое начальное состояние сети,
относительно которого ведётся поиск
Слайд 21
Вывод на основе нечеткой ситуационной сети
Вид подграфа определяется
типом конкретной ситуационной сети:
для сетей, в дугах переходов
которых отсутствует случайная составляющая, обычно принимает вид цепи;
для сетей, учитывающих случайные факторы при переходах, ищется в виде дерева.