- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему по электротехнике на тему конденсатор, его заряд и электрическя емкость
Содержание
- 2. План лекции:Емкость и конденсаторы.Емкость проводников.Емкости различных устройств.Последовательное соединение конденсаторов.Параллельное соединение конденсаторов.Смешанное соединение конденсаторов.
- 3. 1. Емкость и конденсаторы Современные научные представления об
- 4. Впервые принцип действия лейденской банки (конденсатора) был
- 5. 2. Емкость проводников Уединенный заряженный проводник имеет собственное
- 6. Электрическое поле заряженного проводника зависит от его
- 7. Если в диэлектрической среде находятся несколько заряженных
- 8. Рис. 1. Условное обозначение конденсатора постоянной (а)
- 9. где Q – абсолютное значение заряда одного
- 10. Возле условно-графического изображения конденсатора ставят его позиционное
- 11. В радиоэлектронике используются также специальные конденсаторы такие,
- 12. Рис. 5. Внешний вид некоторых электролитических конденсаторов
- 13. Рис. 6. Внешний вид некоторых конденсаторов переменной емкости
- 14. 3. Емкости различных устройств Для расчета емкости конденсатора
- 15. Рис. 7. Плоский конденсатор Приравняв правые
- 16. где εr – относительная диэлектрическая проницаемость находящегося
- 17. 2. Емкость цилиндрического конденсатора. Два концентрических металлических
- 18. 2πℓ εr
- 19. πε0
- 20. расстояние между пластинами 1 мм и между
- 21. 4. Последовательное соединение конденсаторов Последовательное соединение конденсаторов показано на рис. 9.Рис. 9. Последовательное соединение конденсаторов
- 22. После подключения цепи к источнику электрической энергии
- 23. Так как Q = CU, то можно
- 24. или иначе Q/С = Q/С1 + Q/С2
- 25. В частном случае, при последовательном соединении двух
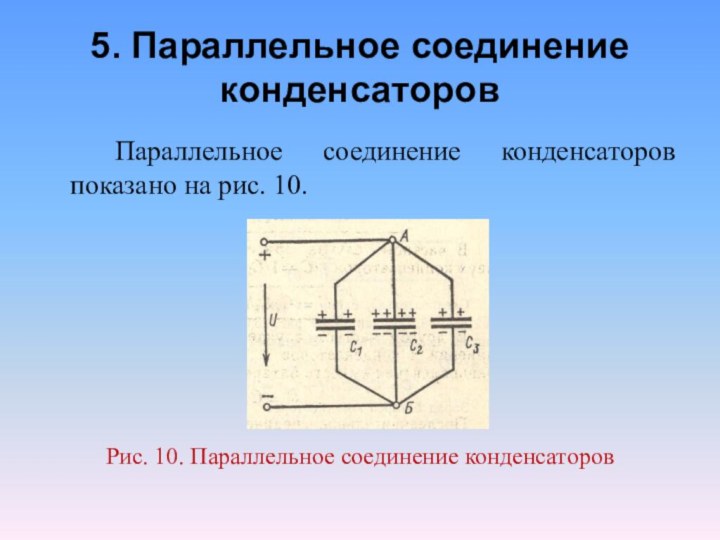
- 26. 5. Параллельное соединение конденсаторов Параллельное соединение конденсаторов показано на рис. 10.Рис. 10. Параллельное соединение конденсаторов
- 27. Напряжение на конденсаторах емкостью С1, С2, С3,
- 28. Если параллельно соединены n конденсаторов с одинаковыми
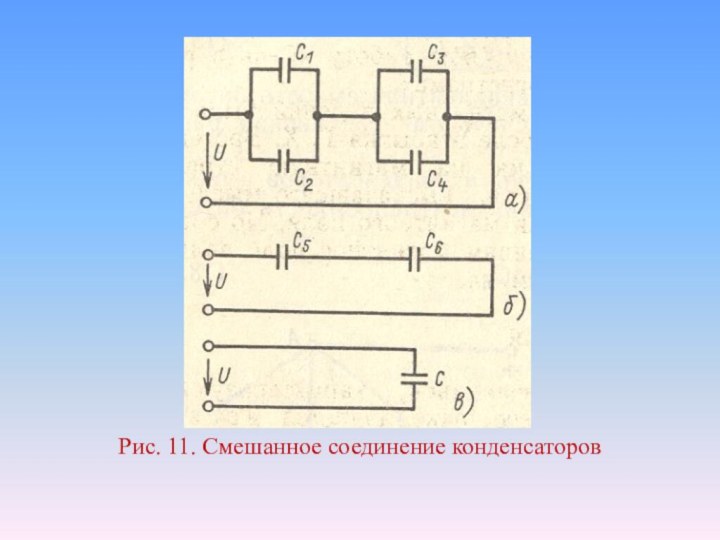
- 29. 6. Смешанное соединение конденсаторов Смешанное соединение конденсаторов представляет
- 30. Задача. Определить эквивалентную емкость и заряд батареи
- 31. Рис. 11. Смешанное соединение конденсаторов
- 32. Следовательно, схему на рис. 11, а можно
- 33. Контрольные вопросы 1. Какую величину называют электрической емкостью?
- 34. Скачать презентацию
- 35. Похожие презентации
План лекции:Емкость и конденсаторы.Емкость проводников.Емкости различных устройств.Последовательное соединение конденсаторов.Параллельное соединение конденсаторов.Смешанное соединение конденсаторов.





























Слайд 2
План лекции:
Емкость и конденсаторы.
Емкость проводников.
Емкости различных устройств.
Последовательное соединение
конденсаторов.
Слайд 3
1. Емкость и конденсаторы
Современные научные представления об электрической
емкости являются результатом многолетней работы ученых разных стран. Изучая
электростатические явления, немецкий ученый О. Герике в 1650 году построил первую электростатическую (емкостную) машину. В 1745 году голландский ученый Мушенбрек изобрел электрический конденсатор – так называемую лейденскую банку. Ученые и любители естествознания, проводя опыты с электростатическими машинами и лейденскими банками, научились соединять банки в батареи и получать сильные электрические разряды.
Слайд 4
Впервые принцип действия лейденской банки (конденсатора) был объяснен
при помощи, так называемой унитарной теории электричества, созданной в
1747 году американским ученым В. Франклином. Согласно этой теории электрические явления объяснялись наличием в телах единой электрической жидкости. Теория Франклина вскоре устарела.
Слайд 5
2. Емкость проводников
Уединенный заряженный проводник имеет собственное электрическое
поле. Поверхность такого проводника является поверхностью равного потенциала, поэтому
можно говорить о потенциале проводника. Для характеристики зависимости потенциала проводника от его электрического поля применяют понятие электрической емкости проводника, или короче, емкости.Электрическая емкость – это физическая величина, характеризующая способность заряженного проводника и окружающей его среды накапливать электрическое поле с его энергией и массой.
Слайд 6
Электрическое поле заряженного проводника зависит от его заряда
Q. Заряд Q и потенциал V уединенного заряженного проводника
связаны зависимостью Q = СV, откуда С = Q / V, где С – емкость проводника. Емкость проводника численно равна заряду, приходящемуся на единицу потенциала проводника.Единица емкость – фарад. Фарад – большая единица, поэтому в практике часто применяют дольные единицы – микрофарад (мкФ) и пикофарад (пФ), где 1 мкФ = 10-6Ф, 1 пФ = 10-12Ф и, наоборот 1 Ф = 106 мкФ; 1 мкФ = 106 пФ.
Слайд 7
Если в диэлектрической среде находятся несколько заряженных проводников,
то у них есть общее электрическое поле. В этом
поле потенциал и заряд каждого из проводников определяются формой, размерами и взаимным расположением проводников и их зарядами. В этом случае говорят о емкости системы проводников. Для практики наибольший интерес представляет система из двух проводников в диэлектрической среде с равными по абсолютному значению и обратными по знаку зарядами +Q и –Q. Такую систему называют конденсатором. Условные обозначения конденсаторов показаны на рис. 1.
Слайд 8
Рис. 1. Условное обозначение конденсатора постоянной (а)
и
переменной (б) емкости
Равным по знаку зарядам проводников соответствуют разные
потенциалы этих проводников V1 и V2, поэтому можно найти напряжение между проводниками U = V1 – V2. Емкость конденсатора определяется соотношением С = Q / U,
Слайд 9
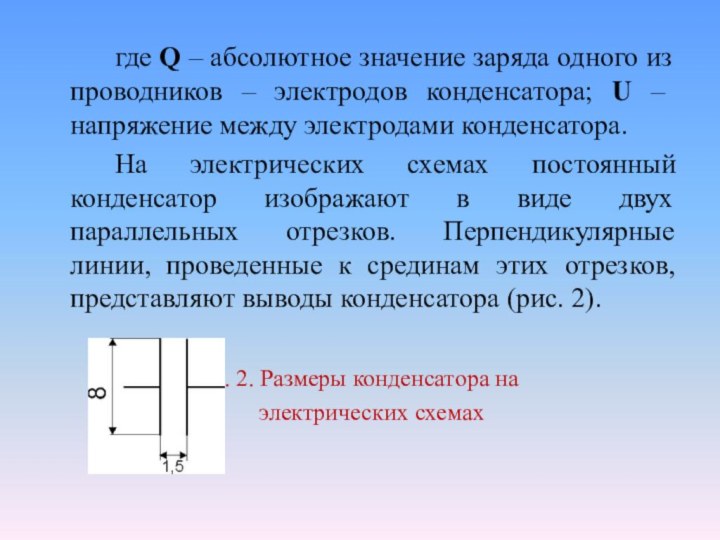
где Q – абсолютное значение заряда одного из
проводников – электродов конденсатора; U – напряжение между электродами
конденсатора.На электрических схемах постоянный конденсатор изображают в виде двух параллельных отрезков. Перпендикулярные линии, проведенные к срединам этих отрезков, представляют выводы конденсатора (рис. 2).
Рис. 2. Размеры конденсатора на
электрических схемах
Слайд 10
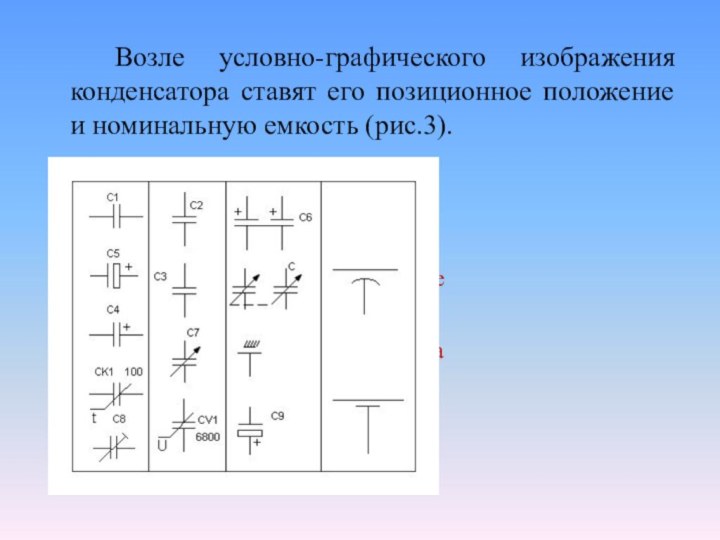
Возле условно-графического изображения конденсатора ставят его позиционное положение
и номинальную емкость (рис.3).
Рис. 3. Позиционное
положение
конденсатора
Слайд 11
В радиоэлектронике используются также специальные конденсаторы такие, как
вариконды, проходные и опорные.
Рис. 4. Внешний вид некоторых конденсаторов
постоянной емкости
Слайд 14
3. Емкости различных устройств
Для расчета емкости конденсатора необходимо
предварительно рассчитать его электрическое поле, например по теореме Гаусса.
1.
Емкость плоского конденсатора. Без учета искажения у краев электродов электрическое поле плоского конденсатора (рис. 7) однородное, его напряженность согласно, ε = σ / εа = Q / S εа, где S – площадь одной пластины – электрода конденсатора. Для однородного электрического поля можно также записать ε = U / d; где U – электрическое напряжение конденсатора; d – расстояние между пластинами.
Слайд 15
Рис. 7. Плоский конденсатор
Приравняв правые части
приведенных выше выражений для напряженности электрического поля, получим U
/ d = Q / S εа или U = Qd / S εа.Для практических расчетов удобнее пользоваться формулой
εr S
С = 8,85 ──── 10-12,
d
С = 8,85
Слайд 16
где εr – относительная диэлектрическая проницаемость находящегося между
пластинами конденсатора диэлектрика; S – в м2; d –
в м. В частности, если между электродами находится воздух, то в надо учесть, что для воздуха εr = 1.Рис. 8. Цилиндрический конденсатор
Слайд 17
2. Емкость цилиндрического конденсатора. Два концентрических металлических цилиндрических
электрода, разделенные диэлектриком, образуют цилиндрический конденсатор (рис. 8). Приводим
без вывода формулу, по которой определяем емкость цилиндрического конденсатора (без учета искажения поля у торцов):2πℓε0 εr
С = ───────
ln (R2/R1)
или
Слайд 18
2πℓ εr
С = 8,85 ─────── 10-12,
ln (R2/R1)где ℓ – длина конденсатора, м; εr – относительная диэлектрическая проницаемость диэлектрика в конденсаторе; R2 и R1 – внутренний и внешний радиусы электродов.
3. Емкость двухпроводной линии. Если пренебречь влиянием земли и неравномерностью распределения зарядов на проводах двухпроводной линии электропередачи, ее емкость на единицу длины (метр) можно определить формулой:
Слайд 19
πε0
С
= ─────
ln (D/r)
или
π
С = 8,85 ───── 10-12,
ln (D/r)
где D – расстояние между осями проводов; r – радиус сечения провода.
Задача. Определить необходимую площадь пластины плоского конденсатора для получения емкости конденсатора, равной 1 Ф, если
Слайд 20
расстояние между пластинами 1 мм и между электродами
конденсатора находится воздух (εа = ε0).
Решение.
CdS = ──── 1012
8,85 εr
По условию εr = 1; d = 10-3 м; С = 1 Ф.
Подставляя эти данные, получаем
Cd 1 ∙ 10-3
S = ──── 1012 = ───── 1012 = 1,13 ∙ 108 м2 = 113 км2.
8,85 εr 8,85 ∙ 1
Слайд 21
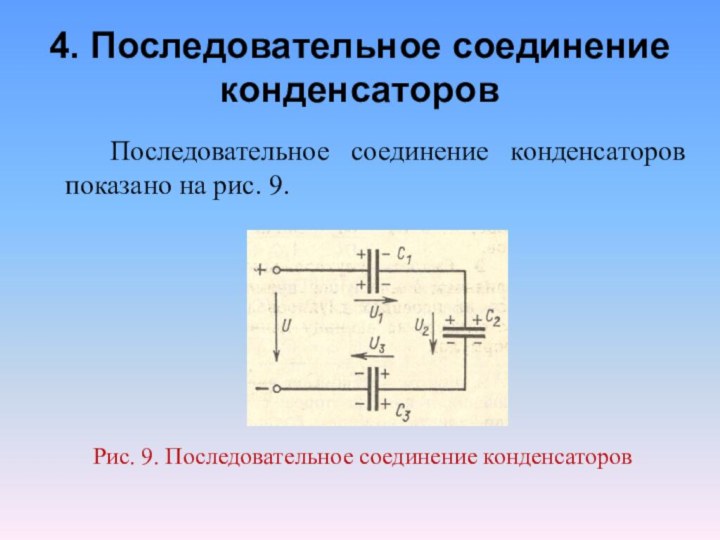
4. Последовательное соединение конденсаторов
Последовательное соединение конденсаторов показано на
рис. 9.
Рис. 9. Последовательное соединение конденсаторов
Слайд 22
После подключения цепи к источнику электрической энергии под
действием электрического поля источника на электрод конденсатора емкостью С1,
крайнего в цепочке, появляется заряд +Q1. Вследствие электростатической индукции другая обкладка этого конденсатора получает такой же по абсолютному значению заряд, но другого знака. От этой обкладки заряжается соседний конденсатор (емкостью С2) и т.д. В результате при последовательном соединении конденсаторов их заряды оказываются одинаковыми, а заряд Q батареи конденсаторов равен заряду одного конденсатора: Q = Q1 = Q2 = Q3 = …
Слайд 23
Так как Q = CU, то можно записать
при последовательном соединении n конденсаторов C1U1 = C2U2 =
C3U3 = … = CnUn = Q, откудаU1 = Q/С1; U2 = Q/С2; … Un = Q/Сn. Напряжения на последовательно соединенных конденсаторах обратно пропорциональны их емкостям.
Согласно второму закону Кирхгофа напряжение на выводах батареи n последовательно соединенных конденсаторов равно сумме напряжений на отдельных конденсаторах: U = U1 + U2 + U3 + … + Un,
Слайд 24
или иначе
Q/С = Q/С1 + Q/С2 +
Q/С2 + Q/С3 + … + Q/Сn,
где С –
эквивалентная емкость батареи конденсаторов. Отсюда 1/С = 1/С1 + 1/С2 + 1/С2 + 1/С3 + … + 1/Сn.При последовательном соединении конденсаторов величина, обратная эквивалентной емкости батареи конденсаторов, равна сумме величин, обратным емкостям отдельных конденсаторов батареи. Находим эквивалентную емкость: 1 1
С = ─── = ──────────────
1/C 1/С1 + 1/С2 + … + 1/ Сn
Слайд 25
В частном случае, при последовательном соединении двух конденсаторов
1/С = 1/С1 + 1/С2, С = С1С2
/ (С1 + С2). В другом частном случае, при последовательном соединении n конденсаторов с одинаковыми емкостями Сn, эквивалентная емкость батареи С = Сn/ n.Последовательное соединение конденсаторов применяют в том случае, когда необходимо иметь батарею, рассчитанную на большее рабочее напряжение, чем номинальное напряжение одного конденсатора батареи, или если необходимая емкость батареи конденсаторов меньше, чем емкость одного конденсатора.
Слайд 26
5. Параллельное соединение конденсаторов
Параллельное соединение конденсаторов показано на
рис. 10.
Рис. 10. Параллельное соединение конденсаторов
Слайд 27
Напряжение на конденсаторах емкостью С1, С2, С3, имеющих
общие узлы А и Б, одно и то же,
т.е. U1 = U2 = U3 = U. Заряды конденсаторов Q1 = C1U, Q2 = C2U, Q3 = C3U.Из рис. 10 видно, что при параллельном соединении заряд батареи параллельно соединенных конденсаторов равен сумме зарядов конденсаторов: Q = Q1 + Q2 + Q3 .
Так как Q = CU = C1U + C2U + C3U,
где С – эквивалентная емкость батареи конденсаторов, то С = С1 + С2 + С3.
Эквивалентная емкость батареи конденсаторов при их параллельном соединении равна сумме емкостей конденсаторов.
Слайд 28
Если параллельно соединены n конденсаторов с одинаковыми емкостями
Cn, то эквивалентная емкость батареи конденсаторов: С = nСn.
Параллельное
соединение конденсаторов применяют, если нужна батарея с емкостью большей, чем емкость одного конденсатора, и с рабочим напряжением, равным номинальному напряжению каждого конденсатора.
Слайд 29
6. Смешанное соединение конденсаторов
Смешанное соединение конденсаторов представляет сочетание
их последовательного и параллельного соединений и рассчитывается по соответствующим
формулам. Расчет смешанного соединения конденсаторов обычно выполняется методом свертывания, подобно тому, как производится расчет смешанного соединения резисторов.Слайд 30 Задача. Определить эквивалентную емкость и заряд батареи конденсаторов,
схема которого показана на рис. 11, а, если напряжение
на входе цепи U = 100 В, а емкость конденсаторов соответственно равны: С1 = 4 мкФ, С2 = 6 мкФ, С3 = 7 мкФ, С4 = 8 мкФ.Решение. На схеме, на рис. 11, а конденсаторы С1 и С2, а также С3 и С4 соединены параллельно. Каждую из этих пар заменим эквивалентными конденсаторами с емкостями С5 и С6:
С5 = С1 + С2 = 4 + 6 = 10 мкФ;
С6 = С3 + С4 = 7 + 8 = 15 мкФ.
Слайд 32
Следовательно, схему на рис. 11, а можно заменить
эквивалентной схемой, показанной на рис. 11, б, где конденсаторы
С5 и С6 соединены последовательно. Эквивалентная емкость батареи С = С5 С6 / (С5 + С6) = 10 ∙ 15 / (10 + 15) = 6 мкФ.Заряд батареи конденсаторов
Q = CU = 6 ∙ 10-6 ∙ 100 = 6 ∙ 10-4 Кл.
Слайд 33
Контрольные вопросы
1. Какую величину называют электрической емкостью? В
каких единицах ее измеряют?
2. Чему равна эквивалентная емкость цепи
при последовательном соединении конденсаторов?3. Как распределяются электрические напряжения на участках цепи при последовательном соединении конденсаторов?
4. Когда применяется последовательное и когда параллельное соединение конденсаторов?
5. Чему равна эквивалентная емкость цепи при параллельном соединении конденсаторов?