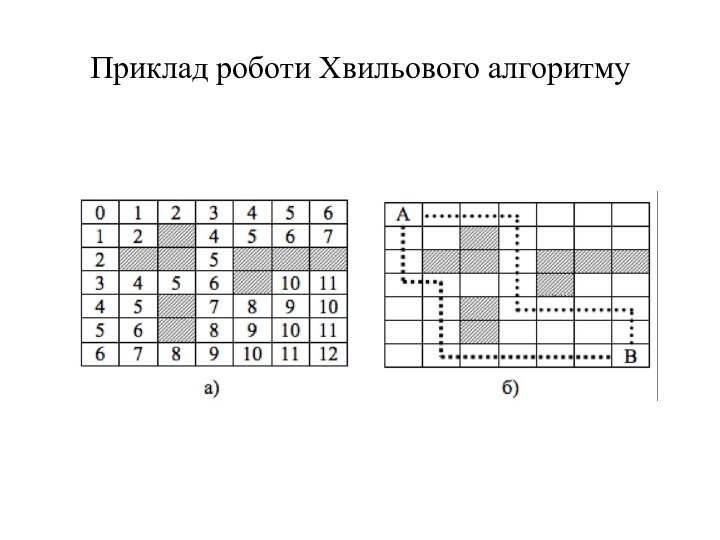
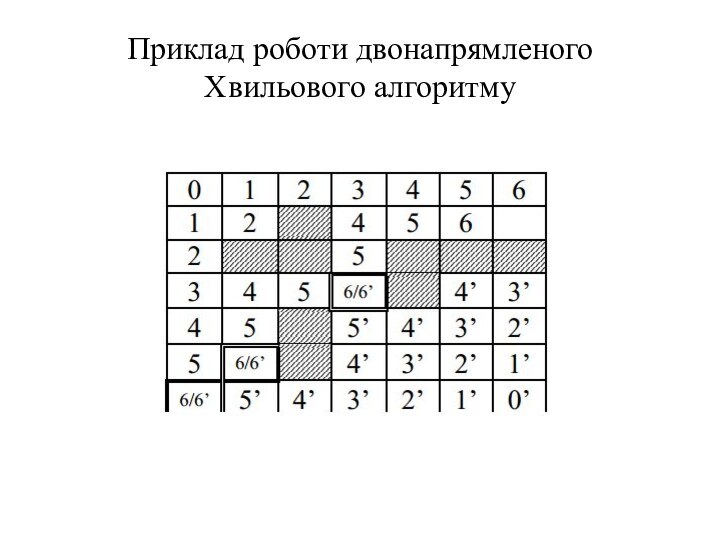
графі з ребрами одиничної довжини. Заснований на алгоритмі пошуку
в ширину. Застосовується для знаходження найкоротшого шляху в графі, в загальному випадку знаходить лише його довжину.Хвильовий алгоритм
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Email: Нажмите что бы посмотреть




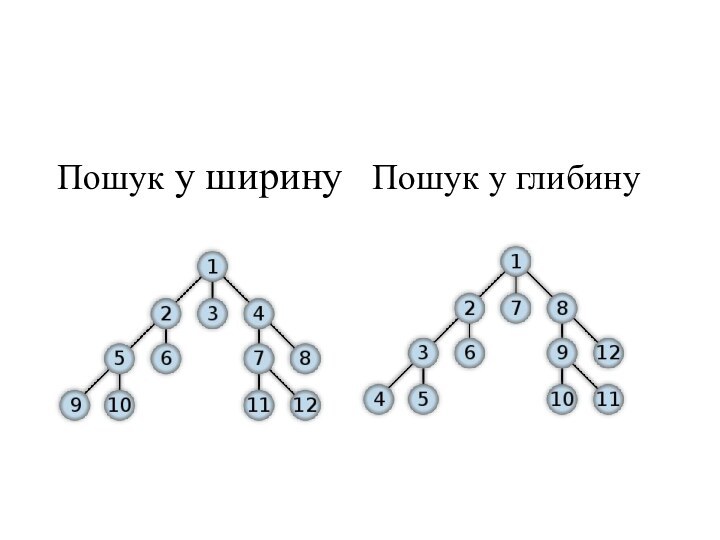







Хвильовий алгоритм
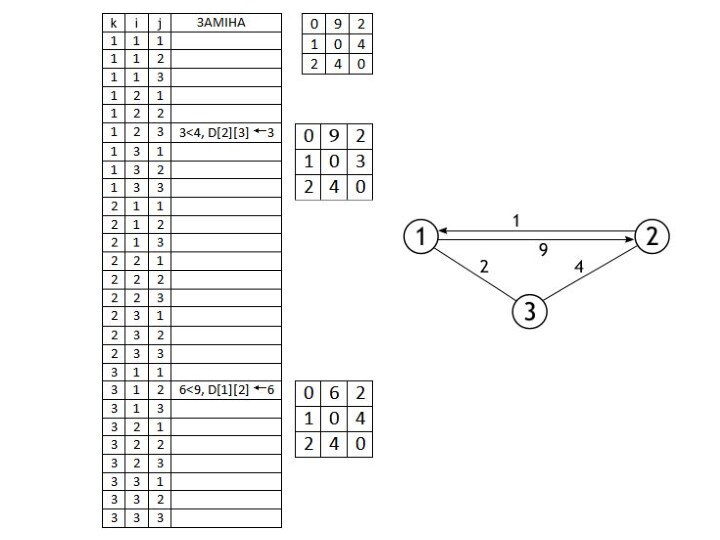
Алгоритм Дейкстри
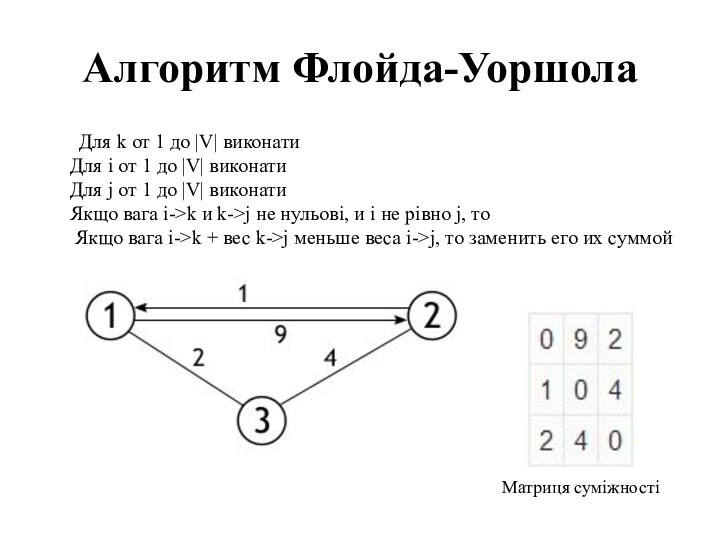
Матриця суміжності