упругостью, т. е. способностью восстанавливать свою форму, искаженную в
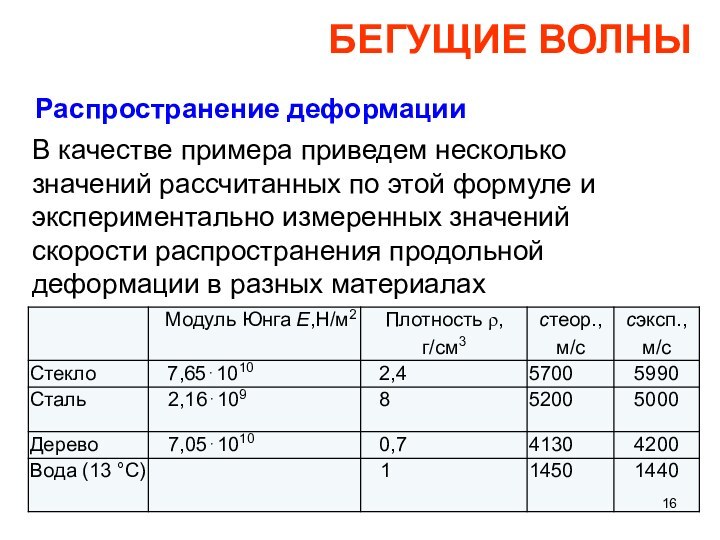
результате кратковременного действия силы. Эта способность тела является причиной того, что всякое механическое действие передается телом с конечной скоростью. Если бы существовал абсолютно твердый, неспособный деформироваться стержень, то он мог бы двигаться только как целое, действие силы распространялось бы по такому телу мгновенно.Распространение деформации
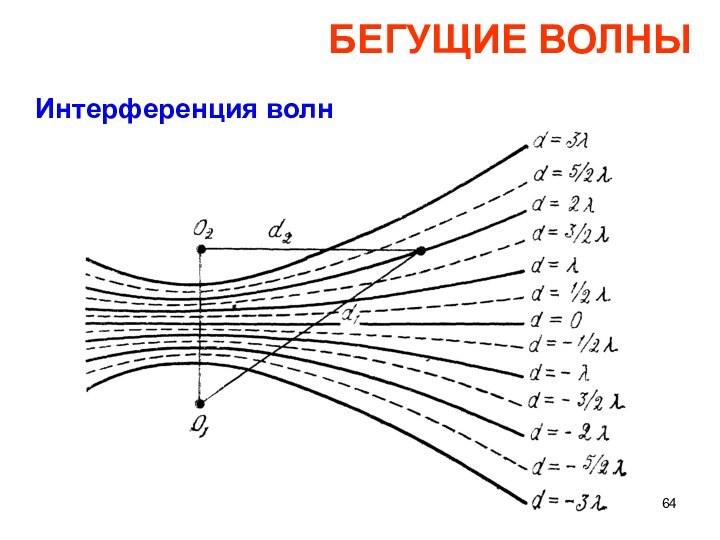
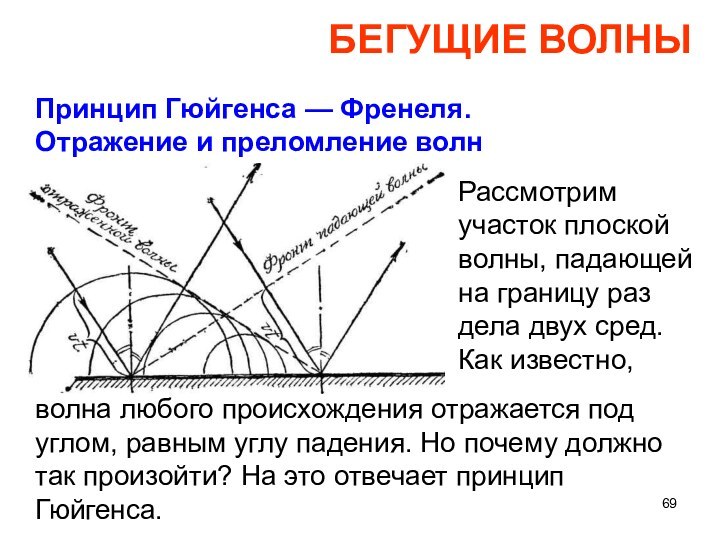
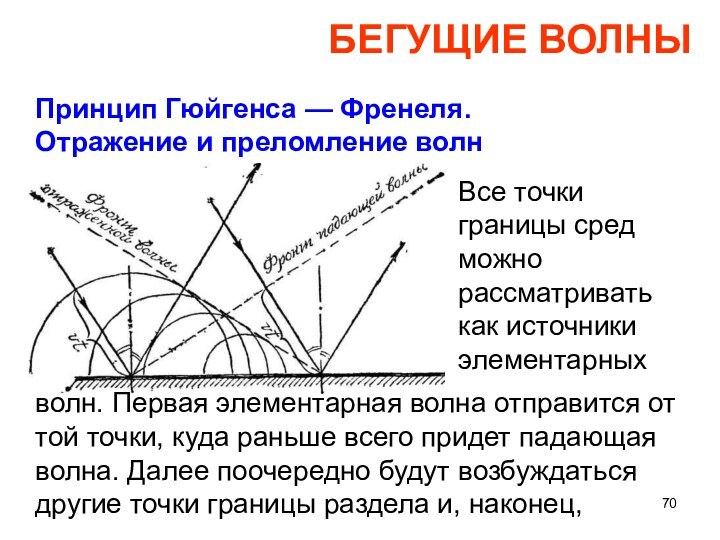
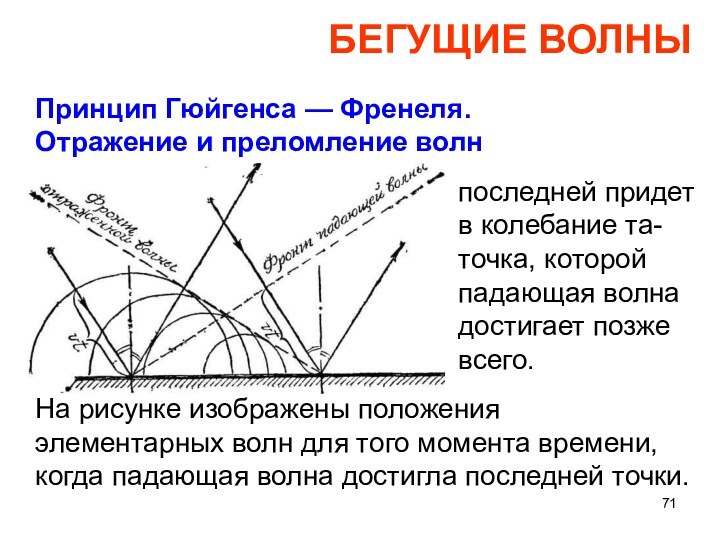
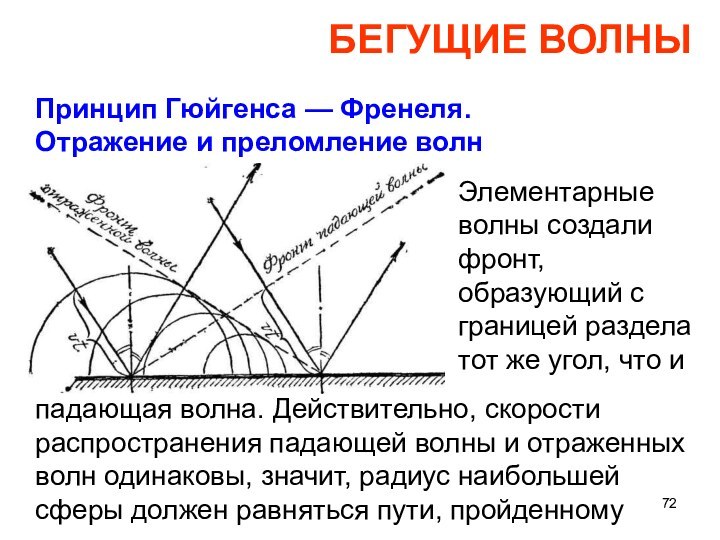
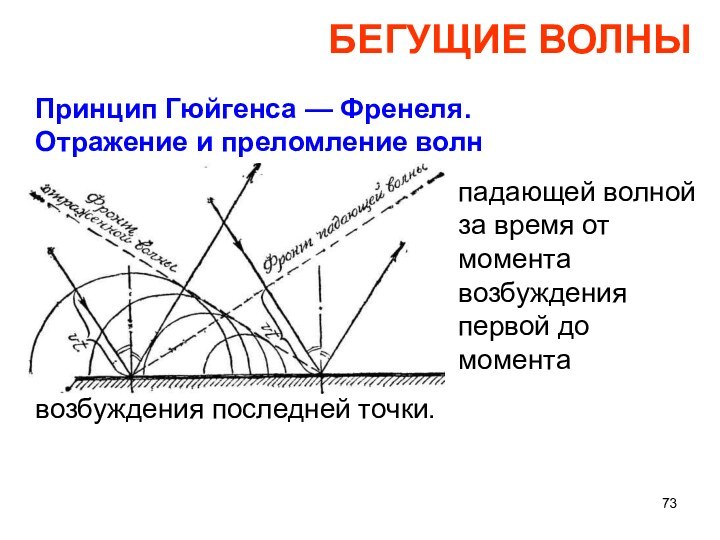
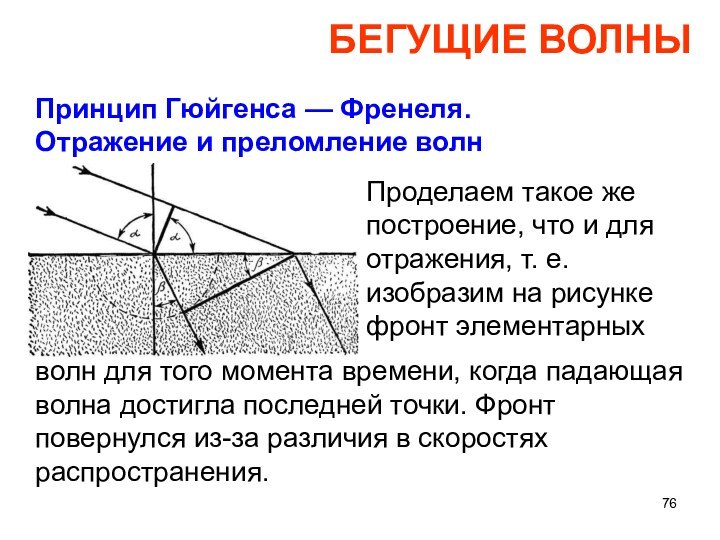
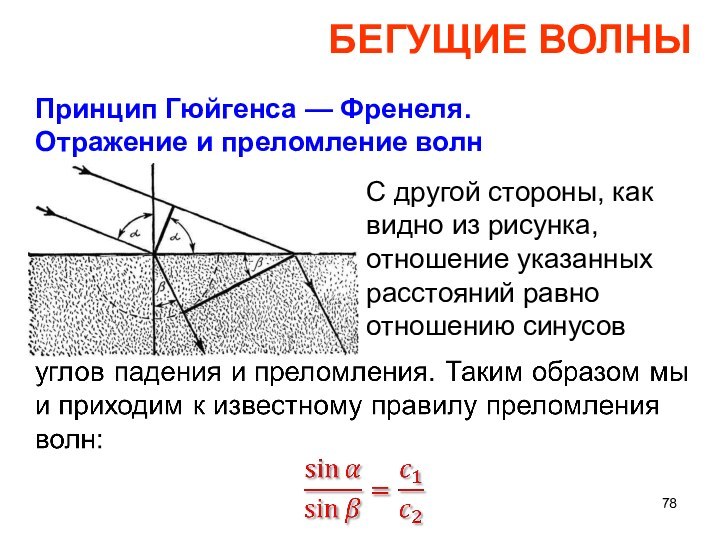
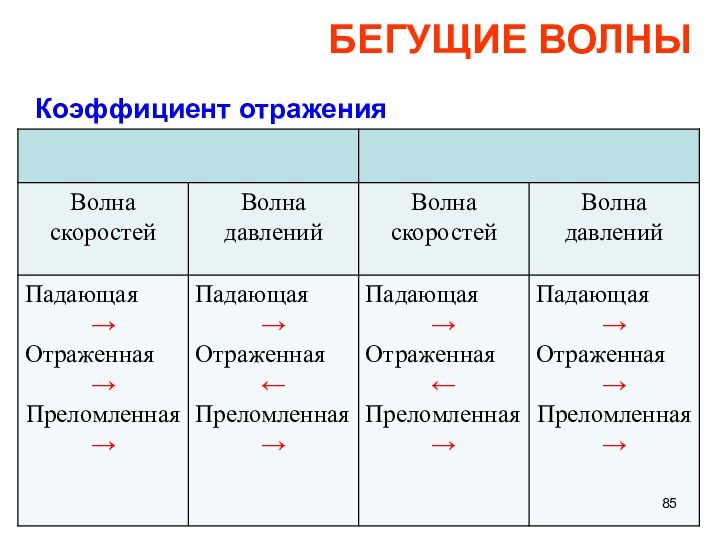
БЕГУЩИЕ ВОЛНЫ