Презентация на тему Логарифмическая

Содержание

2. СОДЕРЖАНИЕ:1. Понятие логарифма. 2. Определение логарифмических функций.3.
3. Логарифмом положительного числа b по положительному и
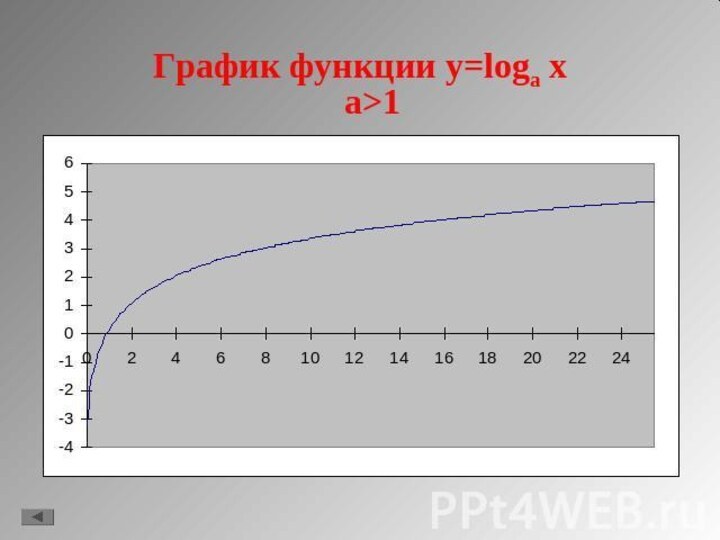
4. Логарифмическая функцияФункция вида Y=LOGa X (где a>0,
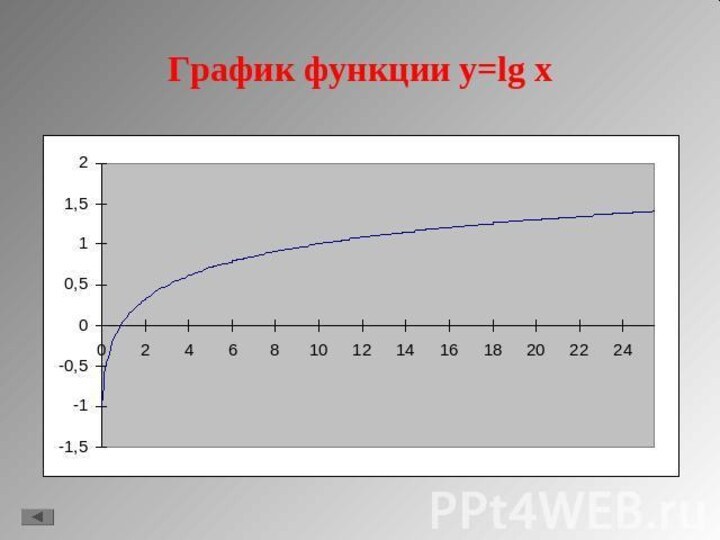
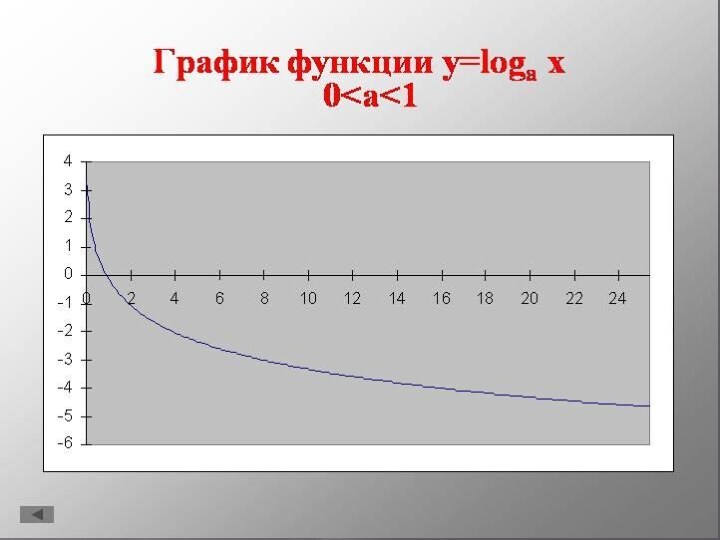
5. Графики логарифмических функции1. y = lg x
10. Свойства f(x)=loga x1. D(f)=(0;+∞); 2. Не является
12. Скачать презентацию
13. Похожие презентации

СОДЕРЖАНИЕ:1. Понятие логарифма. 2. Определение логарифмических функций.3. Графики логарифмических функций. 4. Построение.5. Свойства функции.6. Примеры использования графиков функций.

Логарифмом положительного числа b по положительному и отличному от 1 основанию а

Логарифмическая функцияФункция вида Y=LOGa X (где a>0, a не должно быть =1),

Графики логарифмических функции1. y = lg x 2. y = ln x

Свойства f(x)=loga x1. D(f)=(0;+∞); 2. Не является ни четной, ни нечетной; 3.

Над презентацией работалиБикмулин ХамитКожин МаксимСПАСИБО ЗА ВНИМАНИЕ!

Слайды презентации

Слайд 2 СОДЕРЖАНИЕ:
1. Понятие логарифма.
2. Определение логарифмических функций.
3. Графики

логарифмических функций.
4. Построение.
5. Свойства функции.
6. Примеры использования графиков

функций.

Слайд 3 Логарифмом положительного числа b по положительному и отличному

Логарифмом положительного числа b по положительному и отличному от 1 основанию

от 1 основанию а называют показатель степени, в которую

необходимо возвести число а, чтобы получить число b.

В зависимости от значения основания приняты два обозначения
1. Если основанием является 10, то вместо LOG10 X пишут
lg x.
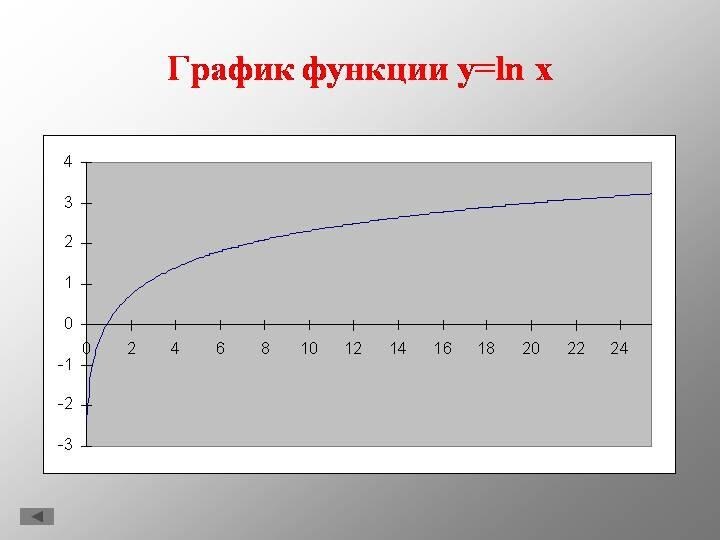
2. Вместо LOGe X принято писать ln x.

Слайд 4 Логарифмическая функция
Функция вида Y=LOGa X (где a>0, a

Логарифмическая функцияФункция вида Y=LOGa X (где a>0, a не должно быть

не должно быть =1), называется логарифмической.
Функция Y=LOGaX принимает значение

, равное нулю, при х=1 и является возрастающей на промежутке x>0,если а>1, и убывающей, если 0Стоит отметить, что график любой логарифмической функции Y=LOGaX проходит через точку (1 ; 0)

Слайд 5 Графики логарифмических функции
1. y = lg x
2.

Графики логарифмических функции1. y = lg x 2. y = ln

y = ln x
3. y = LOGa X,

a>1
4. y = LOGa X, 0

Слайд 6

Слайд 7

Слайд 8

Слайд 9

Слайд 10 Свойства f(x)=loga x
1. D(f)=(0;+∞);
2. Не является ни

Свойства f(x)=loga x1. D(f)=(0;+∞); 2. Не является ни четной, ни нечетной;

четной, ни нечетной;
3. При a>1 функция возрастающая, при

04. Не ограничена;
5. Не имеет ни максимального, ни минимального значения;
6. Непрерывна;
7. E(f)=(- ∞;+ ∞);
8. Выпукла вверх при a>1, выпукла вниз при 0