Что такое findslide.org?

FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.

Обратная связь

Презентация на тему Метод наименьших квадратов.

Содержание

2. Метод наименьших квадратов-математический метод, применяемый для решения
3. МНК является одним из базовых методов регрессионного
5. Плюсы и минусы данного метода.+ он приводит
6. нам нужно подобрать функцию , график которой проходит как
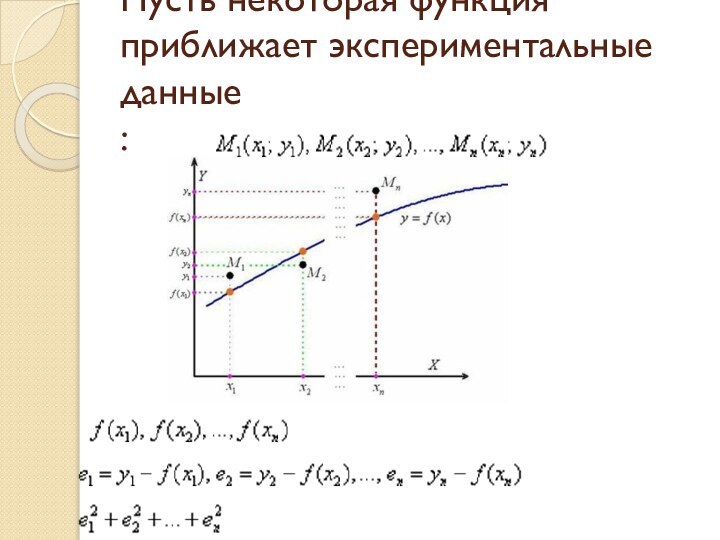
7. Пусть некоторая функция приближает экспериментальные данные
9. Иными словами, задача состоит в нахождении таких
10. Вывод формул для нахождения коэффициентов.
11. Из необходимых условий экстремума следует:
12. Алгоритм МНК:Находим суммы Составляем систему уравнений с
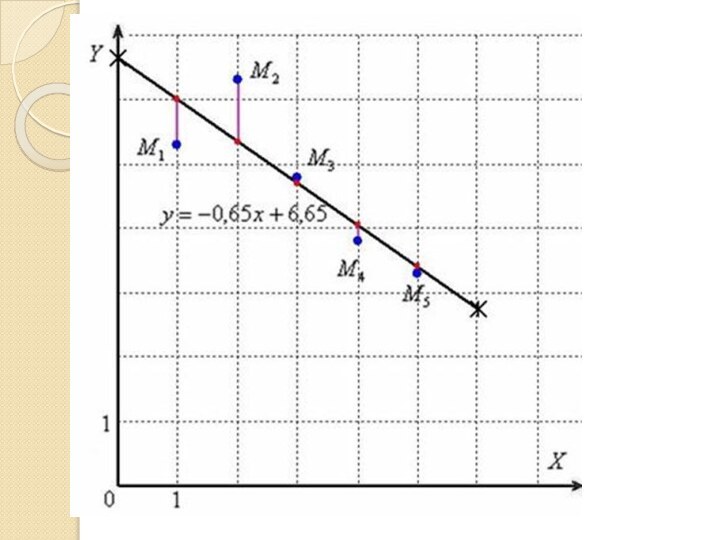
13. Пример:Методом наименьших квадратов найти линейную функцию, которая наилучшим образом приближает эмпирические (опытные) данные.
14. Коэффициенты a, b оптимальной функции y=ax+b найдём как решение системы:
15. Таким образом, получаем следующую систему: .
16. Проверка:Таким образом, искомая аппроксимирующая функция: Для построения
19. Скачать презентацию
20. Похожие презентации

Метод наименьших квадратов-математический метод, применяемый для решения различных задач, основанный на минимизации суммы квадратов отклонений некоторых функций от искомых переменных.

Главная
Разное
Метод наименьших квадратов.

Метод наименьших квадратов.ВыполнилаСтудентка 2 курса, группа с-15-1бИняткина Анна

Метод наименьших квадратов-математический метод, применяемый для решения различных задач, основанный на минимизации

МНК является одним из базовых методов регрессионного анализа для оценки неизвестных параметров

Плюсы и минусы данного метода.+ он приводит к сравнительно простому математическому способу

нам нужно подобрать функцию , график которой проходит как можно ближе к точкам. Такую

Пусть некоторая функция приближает экспериментальные данные

Иными словами, задача состоит в нахождении таких коэффициентов a и b –

Вывод формул для нахождения коэффициентов.

Из необходимых условий экстремума следует:

Алгоритм МНК:Находим суммы Составляем систему уравнений с определённым кол-вом неизвестных. Решаем систему.

Пример:Методом наименьших квадратов найти линейную функцию, которая наилучшим образом приближает эмпирические (опытные) данные.

Коэффициенты a, b оптимальной функции y=ax+b найдём как решение системы:

Таким образом, получаем следующую систему: .

Проверка:Таким образом, искомая аппроксимирующая функция: Для построения графика аппроксимирующей функции найдём два

Слайды презентации

Слайд 2 Метод наименьших квадратов-математический метод, применяемый для решения различных

Метод наименьших квадратов-математический метод, применяемый для решения различных задач, основанный на

задач, основанный на минимизации суммы квадратов отклонений некоторых функций

от искомых переменных.

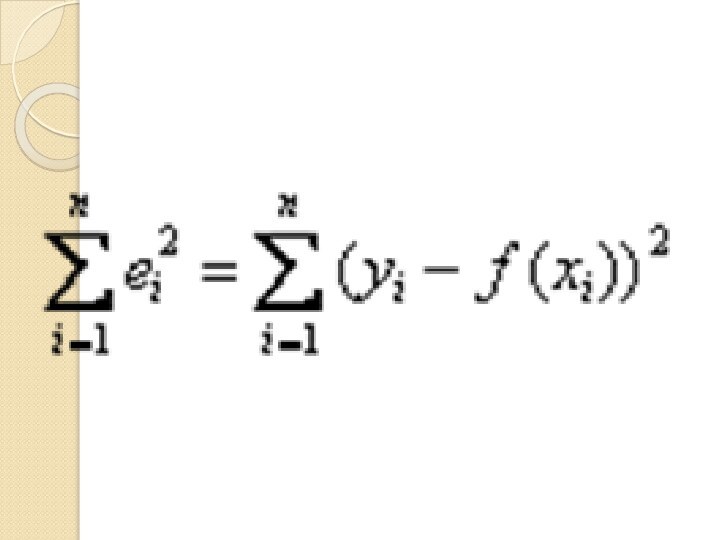
Слайд 3 МНК является одним из базовых методов регрессионного анализа

МНК является одним из базовых методов регрессионного анализа для оценки неизвестных

для оценки неизвестных параметров регрессионных моделей по выборочным данным.
Применяется

также для приближённого представления заданной функции другими (более простыми) функциями и оказывается полезным при обработке наблюдений.

Слайд 4

Слайд 5 Плюсы и минусы данного метода.
+ он приводит к

Плюсы и минусы данного метода.+ он приводит к сравнительно простому математическому

сравнительно простому математическому способу определения параметров а, b, с,

… искомого функционала;
+ он дает довольно веское теоретическое обоснование с вероятностной точки зрения.
- основным недостатком МНК является чувствительность оценок к резким выбросам, которые встречаются в исходных данных.

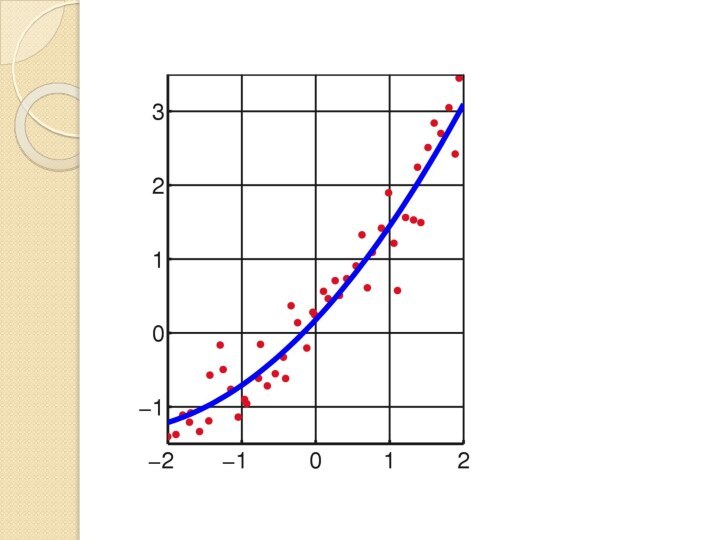
Слайд 6 нам нужно подобрать функцию , график которой проходит как можно

нам нужно подобрать функцию , график которой проходит как можно ближе к точкам.

ближе к точкам. Такую функцию называют аппроксимирующей (аппроксимация – приближение) или теоретической

функцией.

Слайд 7 Пусть некоторая функция приближает экспериментальные данные

Слайд 8

Слайд 9 Иными словами, задача состоит в нахождении таких коэффициентов

a и b – чтобы сумма квадратов отклонений
была

наименьшей.

Слайд 10 Вывод формул для нахождения коэффициентов.

Слайд 11 Из необходимых условий экстремума следует:

Слайд 12 Алгоритм МНК:
Находим суммы
Составляем систему уравнений с определённым

Алгоритм МНК:Находим суммы Составляем систему уравнений с определённым кол-вом неизвестных. Решаем

кол-вом неизвестных.
Решаем систему. (метод Крамера)
В результате получаем стационарную

точку S (искомые коэффициенты a;b)
Вычисляем сумму квадратов отклонений между эмпирическими и теоретическими значениями.

Слайд 13 Пример:
Методом наименьших квадратов найти линейную функцию, которая наилучшим

образом приближает эмпирические (опытные) данные.

Слайд 14 Коэффициенты a, b оптимальной функции y=ax+b найдём как решение системы:

Слайд 15
Таким образом, получаем следующую систему:
.

Слайд 16 Проверка:

Таким образом, искомая аппроксимирующая функция:

Для построения графика

Проверка:Таким образом, искомая аппроксимирующая функция: Для построения графика аппроксимирующей функции найдём

аппроксимирующей функции найдём два её значения:

и выполним чертёж:

Слайд 17

Слайд 18

- Предыдущая Грибковые заболеванияЛишай

Следующая - Неспецифическая противоспалительная терапия

Когнитивные нарушения у больных ишемическим инсультом возможности их коррекции 117

srednyaya 86

Презентация Адаптация детей к условиям детского сада презентация к уроку (младшая группа) 93

франчайзинг в гостиничном бизнесе 144

презентация к внеурочной деятельности 3 класс Старичок Боровичок 36 занятий презентация к уроку (3 класс) 151

ПОДГОТОВКА ПАЦИЕНТА К ОПЕРАЦИИ.ПОСЛЕОПЕРАЦИОННЫЙ ПЕРИОД. 101

Каша - здоровье наше!!!!!!!!!!!! презентация по теме 139

Транспортная логистика 85

Использование интерактивной панели в развитии у детей математических представлений материал (младшая группа) 116

Ребусы Имя прилагательное презентация к уроку (2 класс) 158

ОТКРЫТОЕ ЗАНЯТИЕ ПО ВАЛЕОЛОГИИ в средней группе ОРГАНЫ ЧУВСТ план-конспект занятия (средняя группа) 147

Добро пожаловать, Наурыз! 94

Edv-grundlagen 88

презентация к занятию Путешествие в страну безопасного движения презентация 83

Организация РППС презентация 98

Отгадайте загадки. 112

Предметные декады в начальной школе. презентация к уроку 123

Как приучить ребёнка к самостоятельности в приготовлении уроков. презентация к уроку 131

ОРГАНІЗАЦІЯ, ПЛАНУВАННЯ ТА ЕКОНОМІЧНА ЕФЕКТИВНІСТЬ КОРМОВОЇ БАЗИ 78

Спортивная жизнь школы. 2016-2017 учебный год 117

Презентация Календарные праздники 93

Презентация Экспериментальная деятельность опыты и эксперименты (подготовительная группа) по теме 97

Лекция. Производство в суде кассационной инстанции 101

Поделки своими руками творческая работа учащихся (старшая группа) по теме 119