- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Многогранники
Содержание
- 2. Определение.Многогранником называется тело, граница которого является объединением конечного числа многоугольников.
- 3. Первые упоминания.Первые упоминания о многогранниках известны еще
- 4. Формы многогранников.Многогранники имеют красивые формы, например, правильные,
- 5. История многогранников.История правильных многогранников уходит в глубокую
- 6. Виды многоранников.Существует пять видов правильных многогранников: тетраэдр,
- 7. Правильные многогранники. Все ребра правильного многогранника
- 8. Скачать презентацию
- 9. Похожие презентации
Определение.Многогранником называется тело, граница которого является объединением конечного числа многоугольников.






Слайд 2
Определение.
Многогранником называется тело, граница которого является объединением конечного
числа многоугольников.
Слайд 3
Первые упоминания.
Первые упоминания о многогранниках известны еще за
три тысячи лет до нашей эры в Египте и
Вавилоне. Но теория многогранников является и современным разделом математики. Она тесно связана с топологией, теорией графов, имеет большое значение как для теоретических исследований по геометрии, так и для практических приложений в других разделах математики, например, в алгебре, теории чисел, прикладной математики - линейном программировании, теории оптимального управления.
Слайд 4
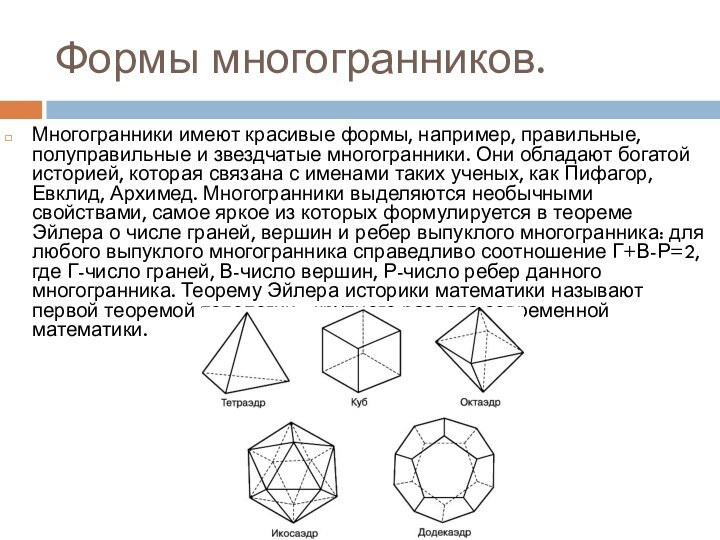
Формы многогранников.
Многогранники имеют красивые формы, например, правильные, полуправильные
и звездчатые многогранники. Они обладают богатой историей, которая связана
с именами таких ученых, как Пифагор, Евклид, Архимед. Многогранники выделяются необычными свойствами, самое яркое из которых формулируется в теореме Эйлера о числе граней, вершин и ребер выпуклого многогранника: для любого выпуклого многогранника справедливо соотношение Г+В-Р=2, где Г-число граней, В-число вершин, Р-число ребер данного многогранника. Теорему Эйлера историки математики называют первой теоремой топологии - крупного раздела современной математики.
Слайд 5
История многогранников.
История правильных многогранников уходит в глубокую древность.
Правильными многогранниками Пифагор и его ученики. Их поражала красота,
совершенство, гармония этих фигур. Пифагорейцы считали правильные многогранники божественными фигурами и использовали в своих философских сочинениях: первоосновам бытия - огню, земле, воздуху, воде придавалась форма соответственно тетраэдра, куба, октаэдра, икосаэдра, а вся Вселенная имела форму додекаэдра. Позже учение пифагорейцев о правильных многогранниках изложил в своих трудах другой древнегреческий ученый, философ - идеалист Платон. С тех пор правильные многогранники стали называться платоновыми телами.
Слайд 6
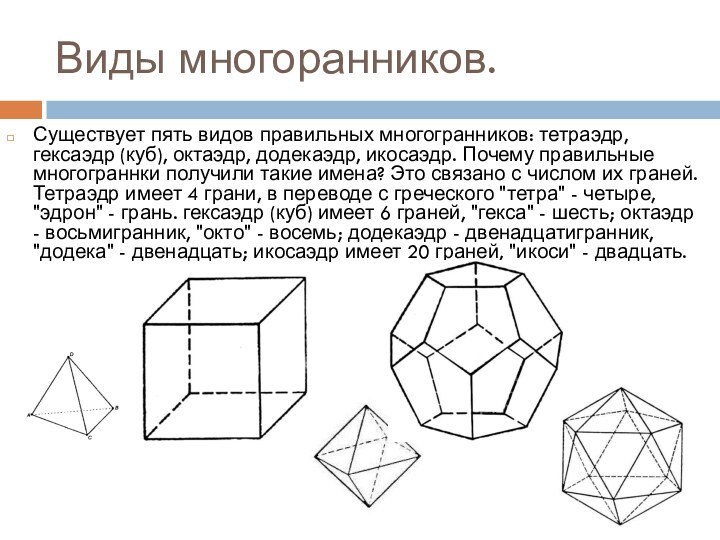
Виды многоранников.
Существует пять видов правильных многогранников: тетраэдр, гексаэдр
(куб), октаэдр, додекаэдр, икосаэдр. Почему правильные многограннки получили такие
имена? Это связано с числом их граней. Тетраэдр имеет 4 грани, в переводе с греческого "тетра" - четыре, "эдрон" - грань. гексаэдр (куб) имеет 6 граней, "гекса" - шесть; октаэдр - восьмигранник, "окто" - восемь; додекаэдр - двенадцатигранник, "додека" - двенадцать; икосаэдр имеет 20 граней, "икоси" - двадцать.
Слайд 7
Правильные многогранники.
Все ребра правильного многогранника — равные отрезки,
все плоские углы правильного многогранника также равны. Существует пять различных
правильных многогранников (выпуклых): правильный четырехгранник (правильный тетраэдр), правильный шестигранник (куб), правильный восьмигранник (правильный октаэдр), правильный двенадцатигранник (правильный додекаэдр), правильный двадцатигранник (правильный икосаэдр).Обозначения: а — длина ребра; V — объем; Sбок — площадь боковой поверхности; Sполн — площадь полной поверхности; R — радиус описанной сферы; r — радиус вписанной сферы; h — высота.



















![Автоматизация звука [С]. Игра Четвертый лишний презентация к уроку по теме](/img/tmb/8/796280/a1185d8d90132b727f77c82d87144953-210x.jpg)









