- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Понятие об умозаключении
Содержание
- 2. Понятие об умозаключенииУмозаключение – это форма мышления,
- 3. Структура умозаключенияПосылки – исходные известные суждения, из
- 4. Классификации умозаключений1)в зависимости от направленности мышления:дедуктивные индуктивныетрадуктивные,
- 5. Условия получения нового истинного знанияпосылки должны быть истинными; 2) должны соблюдаться правила вывода.
- 7. Непосредственные умозаключения вывод делается из одной посылкиобращение, превращение, противопоставление предикату, противопоставление субъекту, умозаключения по «логическому квадрату»
- 8. Превращение (обверсия)
- 9. Примеры превращенияВсе акулы являются рыбами (S a
- 10. Обращение (конверсия)
- 11. Примеры обращенияВсе акулы являются рыбами (S a
- 12. Противопоставление предикату
- 13. Примеры противопоставления предикатуВсе акулы являются рыбами
- 14. Противопоставление субъекту
- 15. Примеры противопоставления субъектуВсе хорьки являются хищниками
- 16. Умозаключения по «логическому квадрату» Все
- 17. Категорический силлогизмУмозаключение, в котором из двух простых
- 18. Термины простого категорического силлогизмаS – субъект
- 19. Фигуры простого категорического силлогизма
- 20. Модусы категорического силлогизмаI фигуры: ААА, ЕАЕ,
- 21. Общие правила категорического силлогизмаПравила посылокИз двух отрицательных
- 22. Правила терминовВ силлогизме должно быть только три
- 23. Специальные правила первой фигурыБольшая посылка всегда является общим суждением.Меньшая посылка всегда является утвердительным суждением.
- 24. Специальные правила второй фигурыБольшая посылка всегда является общим суждением.Одна из посылок – отрицательное суждение.
- 25. Специальные правила третьей фигурыМеньшая посылка является утвердительным суждением. Заключение всегда является частным суждением.
- 26. Специальные правила четвертой фигурыЕсли одна из посылок
- 27. Сокращенный категорический силлогизм (энтимема)
- 28. Восстановление категорического силлогизма из энтимемы.Энтимемы такого типа
- 29. Восстановление энтимемы до полного силлогизмаУстановить, что пропущено
- 30. Восстановление энтимемы«Я – литератор, следовательно, я тощ и легковесен».
- 31. Полисиллогизмсложный силлогизм; соединение нескольких силлогизмов таким образом, что заключение одного силлогизма становится посылкой другого
- 32. Прогрессивный полисиллогизмзаключение просиллогизма становится большей посылкой эписиллогизмаОбщественно
- 33. Регрессивный полисиллогизмзаключение просиллогизма становится меньшей посылкой эписиллогизмаВсе
- 34. СоритПолисиллогизм, в котором пропущено, по крайней мере,
- 35. Эмпихейрема полисиллогизм, состоящий из энтимемЛожь заслуживает презрения,
- 36. Скачать презентацию
- 37. Похожие презентации
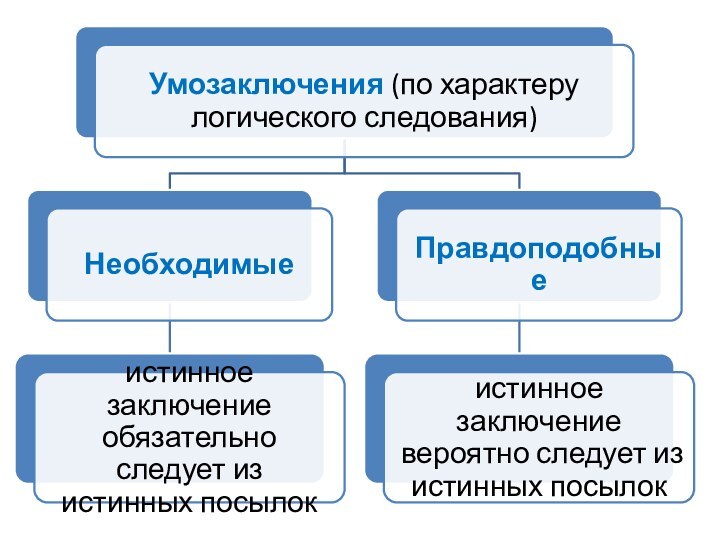
Понятие об умозаключенииУмозаключение – это форма мышления, посредством которой из одного или нескольких суждений выводится новое суждение



































Слайд 2
Понятие об умозаключении
Умозаключение – это форма мышления, посредством
которой из одного или нескольких суждений
выводится новое суждение
Слайд 3
Структура умозаключения
Посылки – исходные известные суждения, из которых
выводится новое суждение.
Заключение (вывод) – новое суждение, полученное логическим
путем из посылок.Связка – логический переход от посылок к заключению.
Слайд 4
Классификации умозаключений
1)в зависимости от направленности мышления:
дедуктивные
индуктивные
традуктивные, или
по аналогии
2)в зависимости от степени строгости вывода:
демонстративные
недемонстративные,
или правдоподобные3)в зависимости от вида суждений, образующих посылки и вывод:
силлогистические, или силлогизмы
несиллогистическими
Слайд 5
Условия получения нового истинного знания
посылки должны быть истинными;
2) должны соблюдаться правила вывода.
Слайд 7
Непосредственные умозаключения
вывод делается из одной посылки
обращение, превращение,
противопоставление предикату, противопоставление субъекту, умозаключения по «логическому квадрату»
Слайд 9
Примеры превращения
Все акулы являются рыбами (S a P).
Все
акулы не являются не рыбами (S e P).
Все
волки, видя Луну, волнуются (S a P).Ни один волк не суть тот, кто не волнуется (остаётся спокоен), видя Луну(S e P).
Слайд 11
Примеры обращения
Все акулы являются рыбами (S a P).
Некоторые
рыбы являются акулами (P i S).
Некоторые владыки Азии падали
с белого слона (S i P).Некоторые из тех, кто падал с белого слона - владыки Азии (P i S).
Слайд 13
Примеры
противопоставления предикату
Все акулы являются рыбами (S a
P).
Все не рыбы не являются акулами (P e S).
Все
нормальные люди не любят,
когда на них кричат (S е P).Некоторые из тех, кто не любит, когда на них кричат, суть нормальные люди (P i S).
Слайд 15
Примеры
противопоставления субъекту
Все хорьки являются хищниками (S a
P).
Некоторые хищники не являются не хорьками (P o
S ).Все нормальные люди не любят, когда на них кричат (S е P).
Все, кто любят, когда на них кричат, суть люди неадекватные (P а S).
Слайд 16
Умозаключения
по «логическому квадрату»
Все подсудимые
виновны
ослабление
отрицание
отрицание
ослабление
Все
подсудимые
не виновны
Некоторые подсудимые виновны
Некоторые подсудимые
не виновны
Слайд 17
Категорический силлогизм
Умозаключение, в котором из двух простых категорических
суждений (посылок), связанных общим термином, получается новое простое категорическое
суждение (заключение)
Слайд 18
Термины простого
категорического силлогизма
S – субъект заключения
Содержится в
заключении и второй (малой) посылке.
Р – предикат заключения
Содержится
в заключении и первой (большой) посылке. М – средний термин
Содержится в первой и второй посылках.
Слайд 20
Модусы категорического силлогизма
I фигуры: ААА, ЕАЕ, АII,
ЕIO
II фигуры: EAЕ, AEE, ЕIO, AOO
III фигуры:
AAI, IAI, AII, EAO, OAO, EIOIV фигуры: AEE, IAI, AAI, EAO, EIO
Слайд 21
Общие правила категорического силлогизма
Правила посылок
Из двух отрицательных посылок
вывода сделать нельзя.
Из двух частных посылок вывода сделать нельзя.
Если
одна из посылок – отрицательное суждение, то заключение должно быть отрицательным.Если одна из посылок – частное суждение, то и заключение должно быть частным.
Слайд 22
Правила терминов
В силлогизме должно быть только три термина.
Средний
термин должен быть распределен хотя бы в одной из
посылок.Термин, не распределенный в посылке, не может быть распределен и в заключении.
Общие правила категорического силлогизма
Слайд 23
Специальные правила первой фигуры
Большая посылка всегда является общим
суждением.
Меньшая посылка всегда является утвердительным суждением.
Слайд 24
Специальные правила второй фигуры
Большая посылка всегда является общим
суждением.
Одна из посылок – отрицательное суждение.
Слайд 25
Специальные правила третьей фигуры
Меньшая посылка является утвердительным суждением.
Заключение всегда является частным суждением.
Слайд 26
Специальные правила четвертой фигуры
Если одна из посылок отрицательная,
то большая посылка – общее суждение.
Если большая посылка –
утвердительное суждение, то меньшая посылка – общее суждение.Если меньшая посылка – утвердительное суждение, то заключение – частное суждение.
Слайд 28
Восстановление категорического силлогизма из энтимемы.
Энтимемы такого типа считаются
корректными, если их можно достроить до правильного силлогизма так,
чтобы пропущенная посылка оказалась истинным высказыванием. В противном случае энтимема будет логически некорректной
Слайд 29
Восстановление энтимемы до полного силлогизма
Установить, что пропущено –
посылка или заключение.
Если пропущена посылка, надо установить, какая из
посылок - большая или меньшая имеется. Зная, какая из посылок опущена, а также зная средний термин можно определить оба термина недостающей посылки, а затем и саму посылку.
Слайд 31
Полисиллогизм
сложный силлогизм; соединение нескольких силлогизмов таким образом, что
заключение одного силлогизма становится посылкой другого
Слайд 32
Прогрессивный полисиллогизм
заключение просиллогизма становится большей посылкой эписиллогизма
Общественно опасное
деяние наказуемо Преступление — общественно опасное деяние.
Преступление наказуемо.
Дача
взятки — преступление.Дача взятки наказуема.
Слайд 33
Регрессивный полисиллогизм
заключение просиллогизма становится меньшей посылкой эписиллогизма
Все планеты
- космические тела.
Сатурн - планета.
Сатурн - космическое тело.
Все космические тела имеют
массу.Сатурн имеет массу.
Слайд 34
Сорит
Полисиллогизм, в котором пропущено, по крайней мере, одно
промежуточное заключение
Англичане — мужественный народ.Мужественный народ свободен.Свободный народ богат.Следовательно,
англичане богатые.
Слайд 35
Эмпихейрема
полисиллогизм, состоящий из энтимем
Ложь заслуживает презрения, т.
к. она безнравственна.
Лесть есть ложь, т. к. она есть
умышленное извращение истины.Лесть заслуживает презрения.