- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Методические рекомендации по использованию нестандартных задач в начальной школе презентация к уроку по теме
Содержание
- 2. “Помогая ученику, учитель должен оказывать ему внутреннюю
- 3. Применение нестандартных задач в обучении
- 4. Основной организационной формой является урок,
- 5. Изучение условия задачиПодготовительная работаСамостоятельная работа учащихсяМетоды решения задачиЭтапы работы над нестандартной задачей:
- 6. Задачи на предположение Анализ условия задач
- 7. Подготовительная работа Цели подготовительной работы:— уточнение
- 8. Подготовительная работа Реши задачу: «На лодочной
- 9. Методы решения задач на предположениеПрактический методРешение данной
- 10. Арифметический метод1) 2•8 = 16 (тур.) —
- 11. Арифметический метод1) 4•8 = 32 (тур.) —
- 12. Алгебраический методОбозначим через x число двухместных лодок,
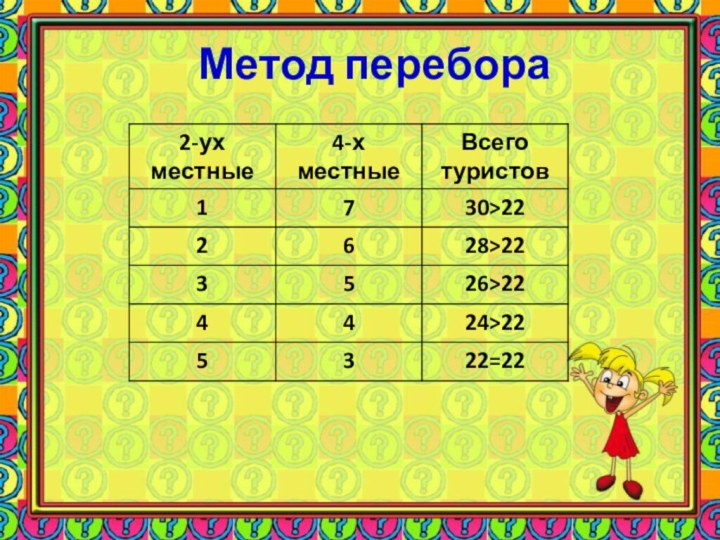
- 13. Метод перебора
- 14. Метод рационального подбораПоскольку общее число лодок равно
- 15. Метод предположения ответаПредположим, что из 8 лодок
- 16. Задачи на предположение1. Для своего участия в
- 17. Предположим, что из 8 лодок только 3
- 18. Скачать презентацию
- 19. Похожие презентации
“Помогая ученику, учитель должен оказывать ему внутреннюю помощь, т.е. ограничиться такими подсказками, которые могли бы рождаться в сознании самого ученика, и избегать внешней помощи, т.е. давать куски решения, которые не связаны с сознанием ученика” (Джордж Пойа).

















Слайд 3 Применение нестандартных задач в обучении младших
школьников математике реализуется в различных формах:
на уроке /на
этапе актуализации знаний, на этапе открытия новых знаний, на этапе включения в систему знаний, при выполнении самостоятельных и контрольных работ, индивидуальных заданий, домашней работы/;во внеклассной работе /кружки, викторины, конкурсы, олимпиады/.
Слайд 4 Основной организационной формой является урок, где
все учащиеся принимают участие в решении нестандартных задач.
Специально обучать детей решению нестандартных задач не нужно /в противном случае такие задачи перестают выполнять свою основную функцию и становятся стандартными/, но знакомить учащихся с некоторыми приемами, облегчающими решение задач, педагогически оправдано.
Слайд 5
Изучение условия задачи
Подготовительная работа
Самостоятельная работа учащихся
Методы решения задачи
Этапы
работы
над нестандартной задачей:
Слайд 6
Задачи на предположение
Анализ условия задач данного
вида приводит к необходимости сопоставления двух (трех и т.
д.) групп объектов, сходных по сути, но имеющих отличительные признаки (например, разное количество ног, колес, страниц и т. п.).Нужно рассадить 22 туриста в двухместные и четырехместные лодки. Сколько тех и других лодок потребуется, если всего лодок 8?
Слайд 7
Подготовительная работа
Цели подготовительной работы:
— уточнение представлений
учащихся об отдельных объектах действительности;
— осознание характера зависимости одной
величины от другой, так как от количества объектов каждого вида зависит суммарное значение их отличительных характеристик.
Слайд 8
Подготовительная работа
Реши задачу: «На лодочной станции
9 двухместных и трехместных лодок. Сколько могло быть лодок
каждого вида? Сколько туристов можно разместить в этих лодках в каждом случае?»
Слайд 9
Методы решения задач на предположение
Практический метод
Решение данной задачи
может быть представлено последовательностью символических рисунков.
Введя соответствующие обозначения и
выполнив практические действия, пересчетом устанавливаем, что если в каждую лодку посадить по 2 туриста, то в 8 лодках разместятся только 16 из 22 человек. Следовательно, 6 туристов разместили по двое (так как лодки были и четырехместные) в первые три лодки. Таким образом находится ответ на вопрос задачи.
Слайд 10
Арифметический метод
1) 2•8 = 16 (тур.) — разместили
по двое в 8 лодках;
2) 22 – 16 =
6 (тур.) — осталось разместить;3) 4 – 2 = 2 (мест) — больше в четырехместной лодке;
4) 6 : 2 = 3 (лод.) — четырехместные;
5) 8 – 3 = 5 (лод.) — двухместных.
Проверка: 2•5 + 4•3 = 22; 22 = 22.
Слайд 11
Арифметический метод
1) 4•8 = 32 (тур.) — разместилось
бы, если все лодки
были бы четырехместные;
2) 32 – 22
= 10 (тур.) — сверх данного в задаче количества;3) 4 – 2 = 2 (мест) — больше в четырехместной лодке, чем
в двухместной;
4) 10 : 2 = 5 (лод.) — двухместных;
5) 8 – 5 = 3 (лод.) — четырехместные.
Слайд 12
Алгебраический метод
Обозначим через x число двухместных лодок, тогда
четырехместных лодок 8 – x. Уравнение, составленное по условию
задачи, примет вид: 2•x + 4•(8 – x) = 22. Решение данного уравнения доступно лишь ученику более старшего школьного возраста.
Слайд 14
Метод рационального подбора
Поскольку общее число лодок равно 8,
то наиболее удачным следует считать подбор, начиная со среднего
варианта — 4 четырехместные лодки и 4 двухместные лодки. А затем, оттолкнувшись от полученного результата (22 туриста), выйти на решение, уменьшив на 1 число четырехместных лодок.Полезно также еще до решения сделать прикидку:
— если бы все лодки были двухместные, то 2•8 = 16 туристов могли бы разместиться в них;
— если бы все лодки были четырехместные, то 4•8 == 32 туриста могли бы разместиться в них.
Данное в условии задачи общее количество туристов (22)
ближе к 16, чем к 32, следовательно, двухместных лодок
было больше, чем четырехместных, например 5 и 3.
Слайд 15
Метод предположения ответа
Предположим, что из 8 лодок только
3 лодки были двухместные, а остальные 5 — четырехместные.
Узнаем, сколько туристов можно рассадить в лодки при этом условии: 2•3 + 4•5 = 26 туристов. Получили, что 26 > 22 (полученное число больше данного общего количества туристов). При принятой гипотезе количество туристов увеличилось бы на 4, так как 26 – 22 = 4. Уберем из каждой четырехместной лодки по 2 туриста, так как в каждой четырехместной лодке на 2 места больше, чем в двухместной (4 – 2 = 2). Теперь узнаем, на сколько принятая гипотеза больше истинного ответа: 4 : 2 = 2 лодки, поэтому количество четырехместных лодок равно 5 – 2 = 3, а двухместных 8 – 3 = 5 или 3 + 2 = 5 лодок. Способом установления соответствия между данными и искомыми легко определяется правильность решения предложенной задачи: 2•5 + 4•3 = 22, 22 = 22.
Слайд 16
Задачи на предположение
1. Для своего участия в школьном
спектакле «Ромео и
Джульетта» Вася купил 10 пуговиц двух видов
— по 3 и по4 р., на общую сумму 34 р. Сколько пуговиц каждого вида
купил Вася?
2*. Имеющийся в магазине центнер картофеля разложили в 26 пакетов по 5 и по 3 кг. Сколько тех и других пакетов потребовалось?
3. Для детского сада купили 10 игрушек на 39 р. 60 к. За каждый мяч заплатили по 3 р. 30 к., а за куклу — по 5 р. 50 к. Сколько купили кукол и сколько мячей?
4. Для уроков труда всем 17 мальчикам 3 класса купили
наборы инструментов. Нужного количества одинаковых наборов в магазине не оказалось, и пришлось купить наборы разных видов — по 63 и по 87 р., на общую сумму 1311 р. Сколько наборов инструментов каждого вида куплено?