- Главная
- Разное
- Бизнес и предпринимательство
- Образование
- Развлечения
- Государство
- Спорт
- Графика
- Культурология
- Еда и кулинария
- Лингвистика
- Религиоведение
- Черчение
- Физкультура
- ИЗО
- Психология
- Социология
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Маркетинг
- Математика
- Медицина
- Менеджмент
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, картинки для презентаций
- Экология
- Экономика
- Юриспруденция
Что такое findslide.org?
FindSlide.org - это сайт презентаций, докладов, шаблонов в формате PowerPoint.
Обратная связь
Email: Нажмите что бы посмотреть
Презентация на тему Проект по исследованиюлинейной функции
Содержание
- 2. Давайте знакомиться!Здравствуйте ! Вас приветствует команда «КВМ(команда
- 3. Мы живем в Коврове . Учимся в 9 школе в 8 "в" классе
- 4. Давайте знакомиться! К математике мы относимся положительно
- 5. Полет – это математика. (В. Чкалов) Наверно
- 6. Давайте знакомиться!Без их труда и любви к
- 7. Кто? Где? Когда? - из истории
- 8. Математика зародилась еще пять тысяч лет назад, когда в Месопотамии впервые изобрели цифры.
- 9. Дальнейшее развитие математика продолжила в эпоху средневековья.
- 10. Переломным для математики стал XVI век. Важнейший шаг к новой математике сделал француз Франсуа Виет
- 11. Он окончательно сформулировал символический метаязык арифметики —
- 12. Так в XVII веке термин «функция»
- 13. В свою очередь, Иоганн Бернулли в письме
- 14. Впоследствии появилось определение функции, данное Эйлером (1751 год)
- 15. затем — у Лакруа (1806 год) — уже практически в современном нам виде
- 16. Наконец, общее определение функции (в современной форме,
- 17. К концу XIX века понятие функции переросло рамки числовых систем. Первыми это сделали векторные функции,
- 18. вскоре Фреге ввёл логические функции (1879)
- 19. После появления теории множеств Дедекинд (1887) и Пеано (1911) сформулировали современное универсальное определение.
- 20. «Что тебе в имени моем?»- о свойствах исследуемой функции.
- 21. «Что тебе в имени моем?»- о свойствах
- 22. «Что тебе в имени моем?»- о свойствах
- 23. «Что тебе в имени моем?»- о свойствах
- 24. «дайте мне функцию – и я объясню
- 25. Например, по закону Гука при небольших удлинениях
- 26. о функциях и физических законах Другой пример:
- 27. «ищите функцию»- о практическом применении функции.1.Автомобиль, выехавший
- 28. «ищите функцию»- о практическом применении функции.2.Свеча длиной
- 29. «ищите функцию»- о практическом применении функции.3. Отправляя
- 30. «ищите функцию»- о практическом применении функции.4. Из
- 31. Заключение.Конечно, каждый раз надо думать об области
- 32. Скачать презентацию
- 33. Похожие презентации
Давайте знакомиться!Здравствуйте ! Вас приветствует команда «КВМ(команда веселых математиков)".Наша команда состоит из двух человек : Красновой Яны и Фонаревой Анны.


























Слайд 4
Давайте знакомиться!
К математике мы относимся
положительно .
Она помогает хорошо развивать логическое
мышление.
Математика - это скорее
помощница всех наук, само по себе её существование абстрактно, но в связке с другими науками , она может творить чудеса . Мы всегда любили эту науку.
Слайд 5
Полет – это математика. (В. Чкалов)
Наверно ,потому,
что у нас всегда проявлялся к ней интерес. А
главное ,что нам просто повезло с учителями по этому предмету в школе.
Слайд 6
Давайте знакомиться!
Без их труда и любви к этой
науке, и методов донесения до учеников необходимости
знания этого
предмета и раскрытие самого предмета наверно , все было бы по - другому.Евгения Викторовна Зинина
Наша учительница по математике
Слайд 7
Кто? Где? Когда? - из истории
возникновения функции
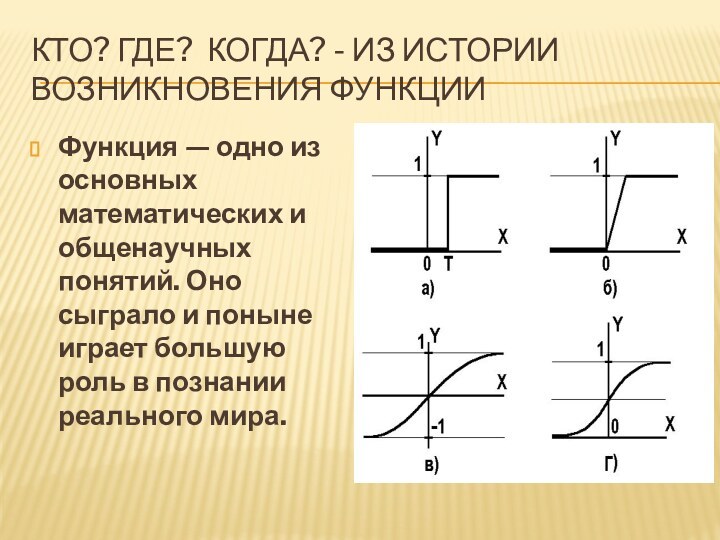
Функция
— одно из основных математических и общенаучных понятий. Оно
сыграло и поныне играет большую роль в познании реального мира.Слайд 9 Дальнейшее развитие математика продолжила в эпоху средневековья. Около
500 года н. э. неизвестный нам великий индийский математик
изобрёл новую систему записи чисел — десятичную позиционную систему.Слайд 10 Переломным для математики стал XVI век. Важнейший шаг
к новой математике сделал француз Франсуа Виет
Слайд 11 Он окончательно сформулировал символический метаязык арифметики — буквенную
алгебру
Благодаря символике Виета (впоследствии символики Декарта) стало возможным появление
функции.Слайд 12 Так в XVII веке термин «функция» (в
некотором более узком смысле) был впервые использован Лейбницем (1692
год).Слайд 13 В свою очередь, Иоганн Бернулли в письме к
тому же Лейбницу употребил этот термин в смысле, более
близком к современному.Иоганн Бернулли
Слайд 16 Наконец, общее определение функции (в современной форме, но
для числовых функций) было дано Лобачевским (1834 год) и
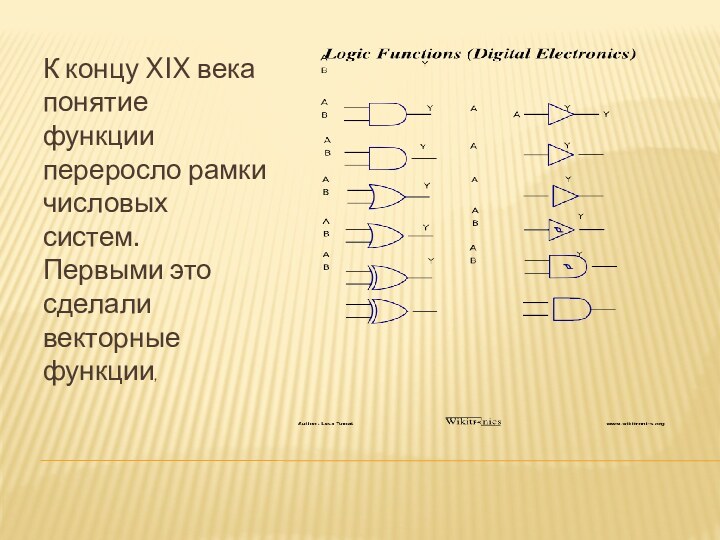
Дирихле (1837 год)Слайд 17 К концу XIX века понятие функции переросло рамки
числовых систем. Первыми это сделали векторные функции,
Слайд 19 После появления теории множеств Дедекинд (1887) и Пеано
(1911) сформулировали современное универсальное определение.
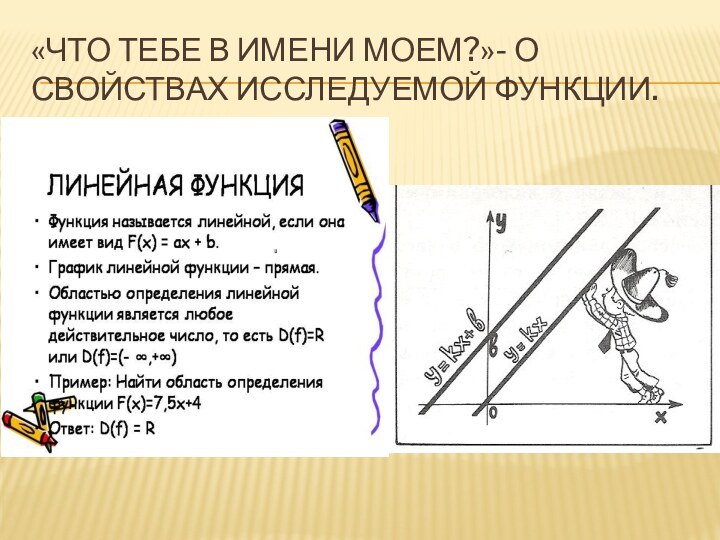
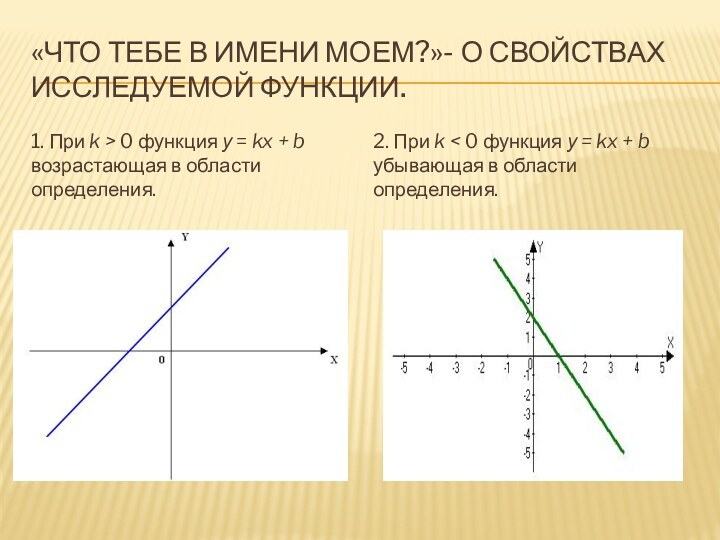
Слайд 21 «Что тебе в имени моем?»- о свойствах исследуемой
функции.
1. При k > 0 функция у = kx
+ b возрастающая в области определения.2. При k < 0 функция у = kx + b убывающая в области определения.
Слайд 22 «Что тебе в имени моем?»- о свойствах исследуемой
функции.
3. Множеством значений функции y = kx + b(k
≠ 0) является вся числовая прямая, т.е. множество R действительных чисел.При k = 0 множество значений функции у = kx + b состоит из одного числа b.
Графиком линейной функции у = b является прямая, проходящая через точку (0; b) и параллельная оси Ох.
Слайд 23 «Что тебе в имени моем?»- о свойствах исследуемой
функции.
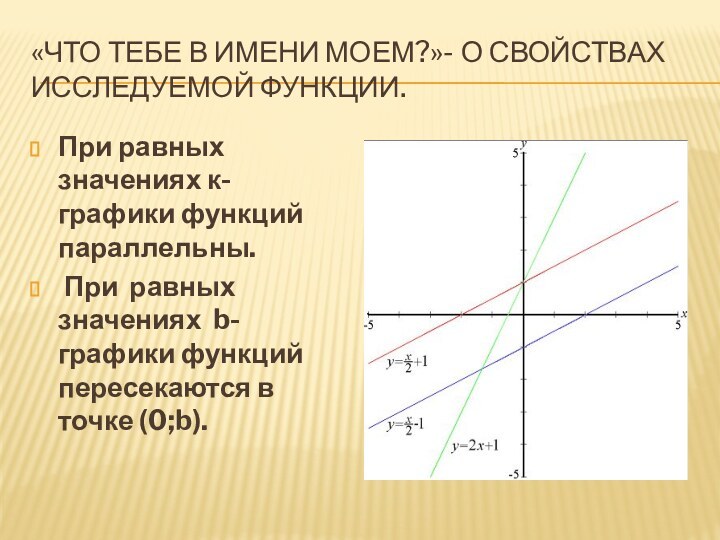
При равных значениях к- графики функций параллельны.
При равных
значениях b- графики функций пересекаются в точке (0;b).Слайд 24 «дайте мне функцию – и я объясню этот мир»-
о функциях и физических законах
Линейная функция простейшая и, можно
сказать, важнейшая среди всех функций. Многие физические законы выражаются с помощью линейной функции , но важно то, что целый ряд сложных нелинейных зависимостей «в малом» можно считать линейными. Слайд 25 Например, по закону Гука при небольших удлинениях (и
только при них) сила упругости F пропорциональна величине x
- удлинению пружины: F= -kx . о функциях и физических законах
Слайд 26
о функциях и физических законах
Другой пример: напряжение
V по закону Ома линейно зависит от силы тока
J , именно V=RJ (здесь R – сопротивление), однако этот закон также справедлив лишь при не очень больших изменениях силы тока.
Слайд 27
«ищите функцию»- о практическом применении функции.
1.Автомобиль, выехавший из
пункта А, в настоящее время находится от него в
120 км. На каком расстоянии s от А будет находиться автомобиль через tч, если он будет двигаться в том же направлении со скоростью 50 км/ч? Ответ будет выражаться линейной функцией видаs = 50 t + 120 .
Слайд 28
«ищите функцию»- о практическом применении функции.
2.Свеча длиной 25
см при горении уменьшается на 1,5 см за каждый
час. Нетрудно сообразить, что ее длина l через t часов будет составлятьl = 25 - 1,5t .
Слайд 29
«ищите функцию»- о практическом применении функции.
3. Отправляя телеграмму,
мы платим по 3 к. за каждое слово и
10 к. дополнительно. Общая стоимость телеграммы выражается линейной функциейe = 3 x + 10.
Слайд 30
«ищите функцию»- о практическом применении функции.
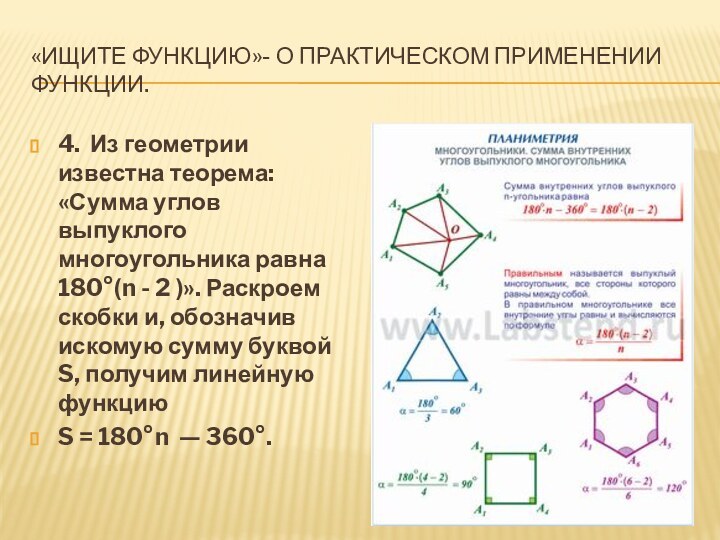
4. Из геометрии
известна теорема: «Сумма углов выпуклого многоугольника равна 180°(n -
2 )». Раскроем скобки и, обозначив искомую сумму буквой S, получим линейную функциюS = 180°n — 360°.