Слайд 2
История
Проблема четырёх красок — математическая задача, предложенная Ф. Гутри (англ.) в 1852
году, сформулированная следующим образом:
«Выяснить, можно ли всякую расположенную на сфере карту
раскрасить четырьмя красками так, чтобы любые две области, имеющие общий участок границы, были раскрашены в разные цвета».
Две необходимые характеристики этой карты:
Граница между любыми двумя областями является непрерывной линией.
Каждая область является односвязной.
Слайд 3
Принцип
В приложениях теории графом нередко возникают задачи, для
решения которых необходимо разбить множество всех вершин графа в
объединение непустых непересекающихся подмножеств таким образом, чтобы вершины из одного и того же множества были попарно не смежными, а число таких подмножеств – минимально возможным. При решении таких задач можно представить себе, что мы раскрашиваем вершины графа в различные цвета, причем сделать это надо так, чтобы любые две смежные вершины были раскрашены в разные цвета, а число использованных цветов было минимально возможным.
Слайд 4
Что это?
Вершинной раскраской графа называется отображение множества вершин графа
на конечное множество (цветов);
n-раскраска графа - раскраска с использованием n цветов.
Раскраска
называется правильной, если никакие две вершины одного цвета не смежны.
Для графа без петель всегда существует правильная раскраска в |V| цветов.
Слайд 5
Хроматическое число
Задача о раскраске состоит в нахождении правильной
раскраски данного графа G в наименьшее число цветов. Это число
называется хроматическим числом графа G и обозначается X(G).
Хроматическое число является единственным.
Хроматическое число нельзя вычислить, зная только его стандартные числовые характеристики (число вершин, ребер, компонент связности, распределение степеней вершин…)
Слайд 6
Лемма о раскраске циклов
Хроматическое число всякого цикла, содержащего
n вершин, равно 2, если n четно, и 3,
если n нечетно.
Следствие
Если граф G содержит цикл нечетной длины, то X(G)>2
Слайд 7
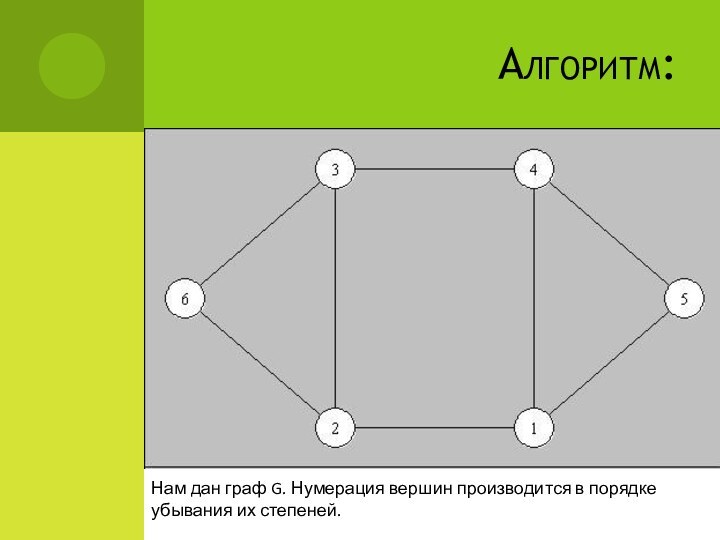
Алгоритм:
Нам дан граф G. Нумерация вершин производится в
порядке убывания их степеней.
Слайд 8
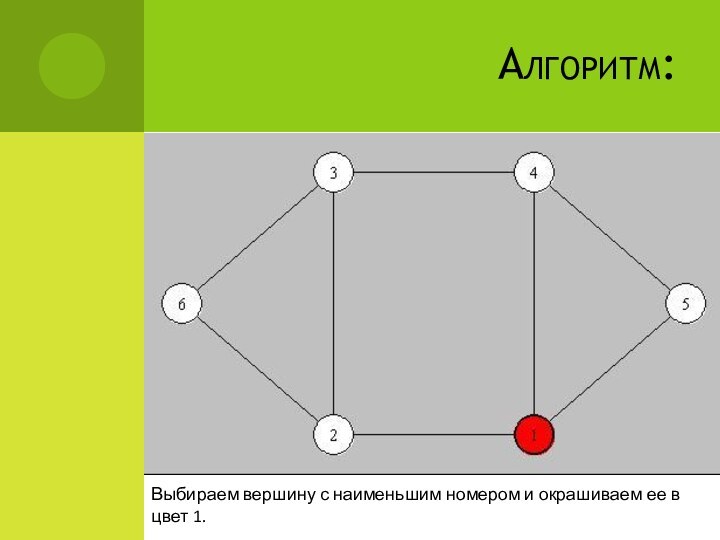
Алгоритм:
Выбираем вершину с наименьшим номером и окрашиваем ее
в цвет 1.
Слайд 9
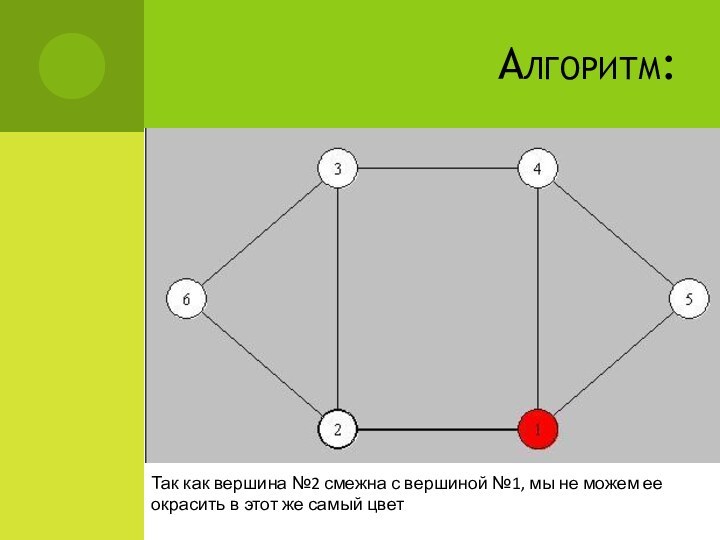
Алгоритм:
Так как вершина №2 смежна с вершиной №1,
мы не можем ее окрасить в этот же самый
цвет
Слайд 10
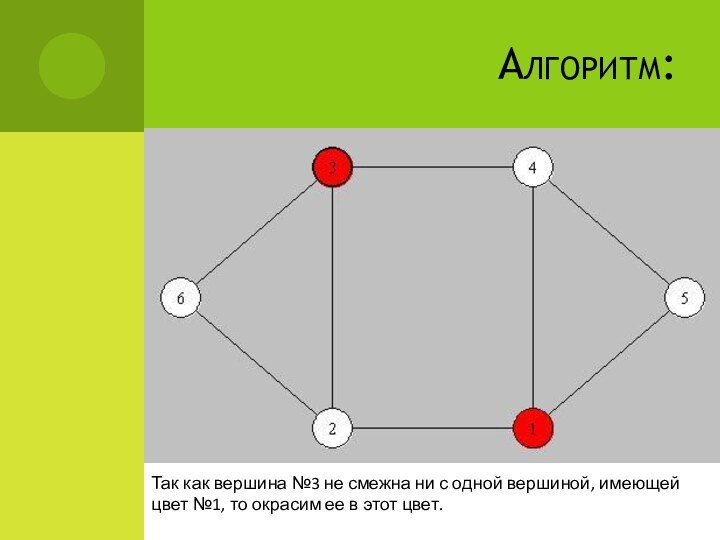
Алгоритм:
Так как вершина №3 не смежна ни с
одной вершиной, имеющей цвет №1, то окрасим ее в
этот цвет.
Слайд 11
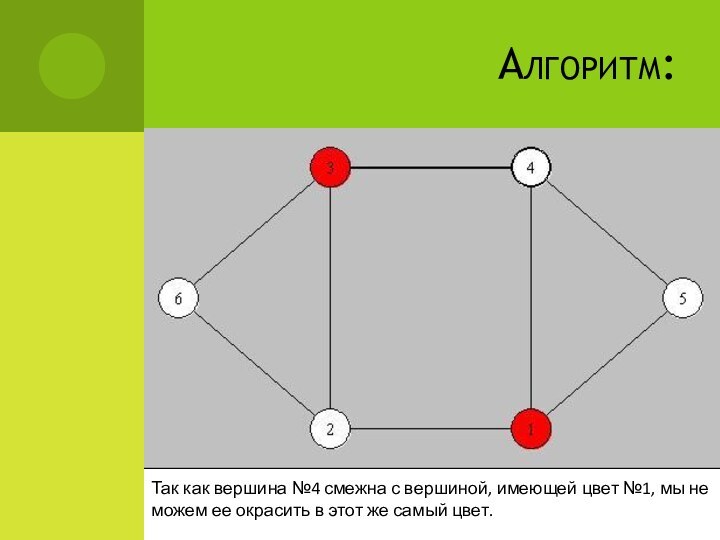
Алгоритм:
Так как вершина №4 смежна с вершиной, имеющей
цвет №1, мы не можем ее окрасить в этот
же самый цвет.
Слайд 12
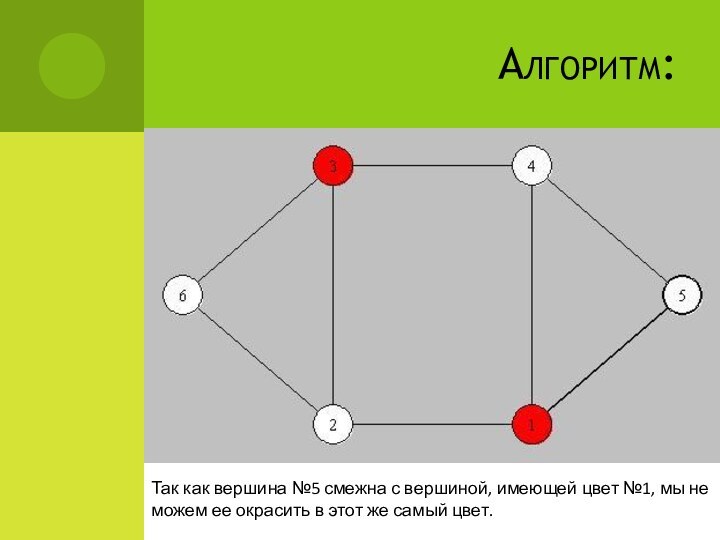
Алгоритм:
Так как вершина №5 смежна с вершиной, имеющей
цвет №1, мы не можем ее окрасить в этот
же самый цвет.
Слайд 13
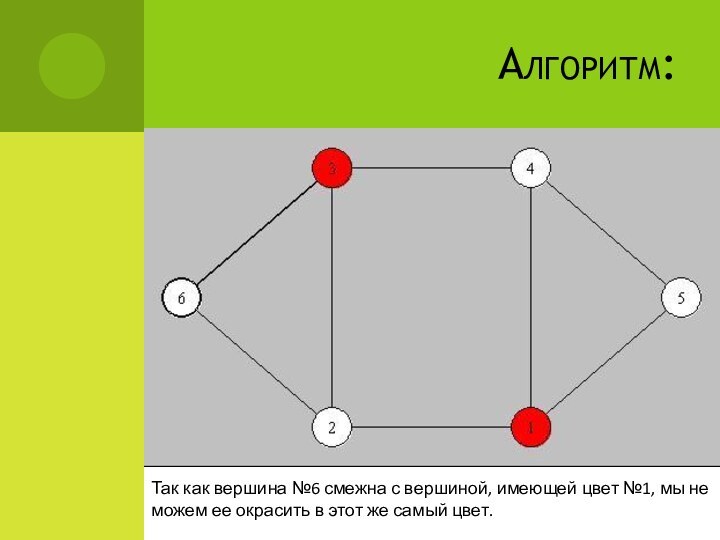
Алгоритм:
Так как вершина №6 смежна с вершиной, имеющей
цвет №1, мы не можем ее окрасить в этот
же самый цвет.
Слайд 14
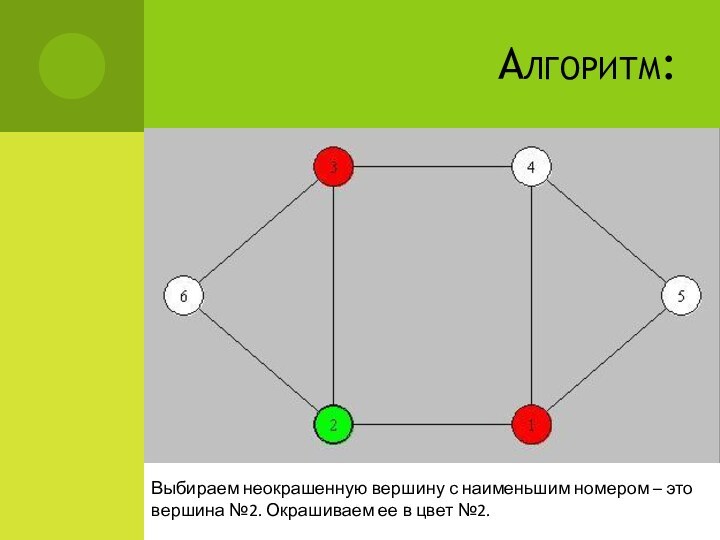
Алгоритм:
Выбираем неокрашенную вершину с наименьшим номером – это
вершина №2. Окрашиваем ее в цвет №2.
Слайд 15
Алгоритм:
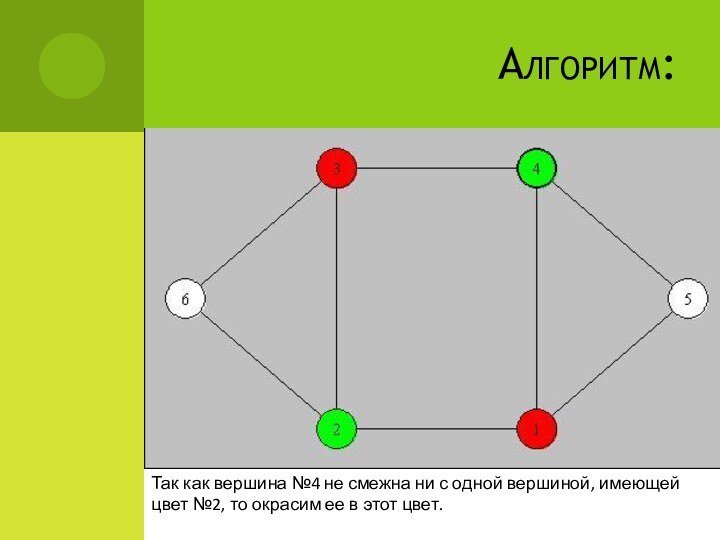
Так как вершина №4 не смежна ни с
одной вершиной, имеющей цвет №2, то окрасим ее в
этот цвет.
Слайд 16
Алгоритм:
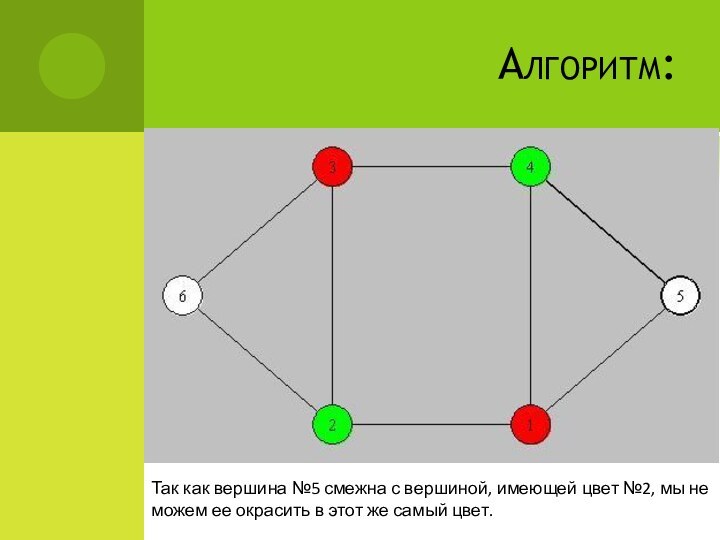
Так как вершина №5 смежна с вершиной, имеющей
цвет №2, мы не можем ее окрасить в этот
же самый цвет.
Слайд 17
Алгоритм:
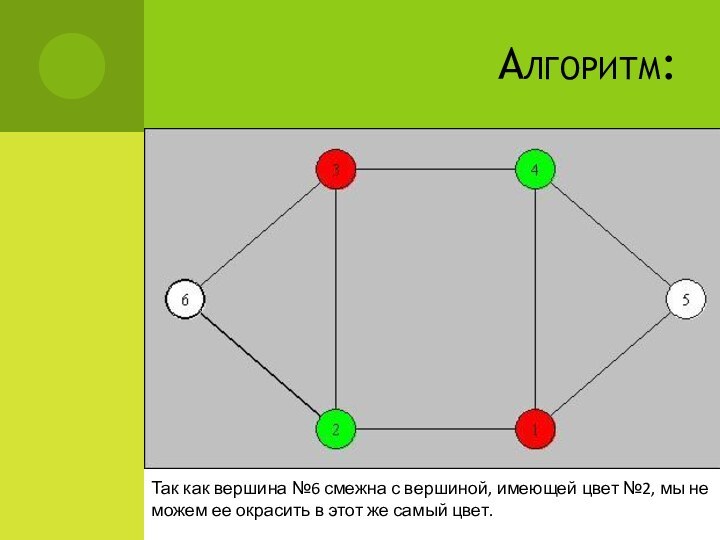
Так как вершина №6 смежна с вершиной, имеющей
цвет №2, мы не можем ее окрасить в этот
же самый цвет.
Слайд 18
Алгоритм:
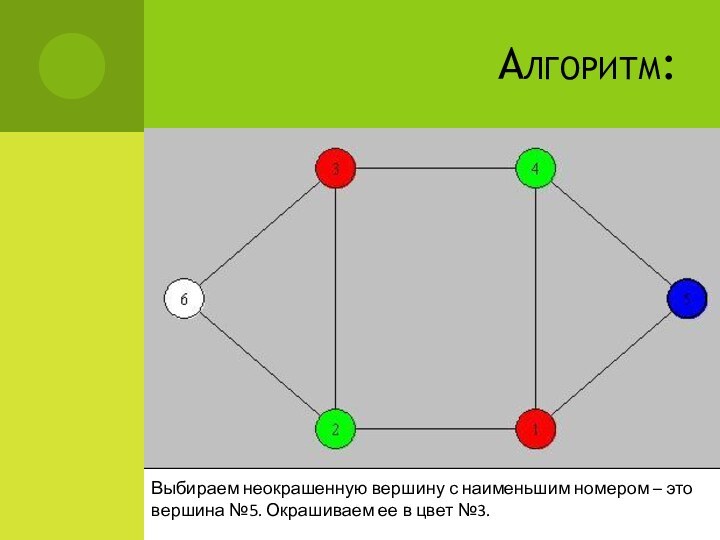
Выбираем неокрашенную вершину с наименьшим номером – это
вершина №5. Окрашиваем ее в цвет №3.
Слайд 19
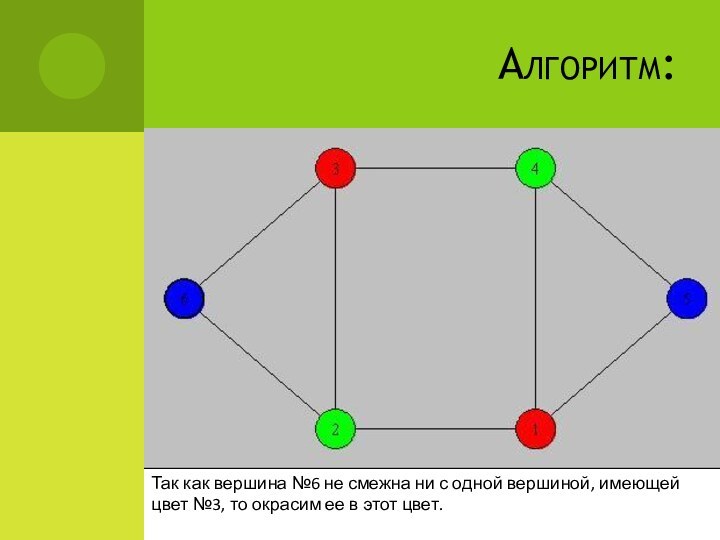
Алгоритм:
Так как вершина №6 не смежна ни с
одной вершиной, имеющей цвет №3, то окрасим ее в
этот цвет.
Слайд 20
Применение
Составление расписаний
расписания для образовательных учреждений
расписания в спорте
планирование встреч, собраний,
интервью
расписания транспорта, в том числе — авиатранспорта
расписания для коммунальных служб