Презентация на тему Сложение колебаний

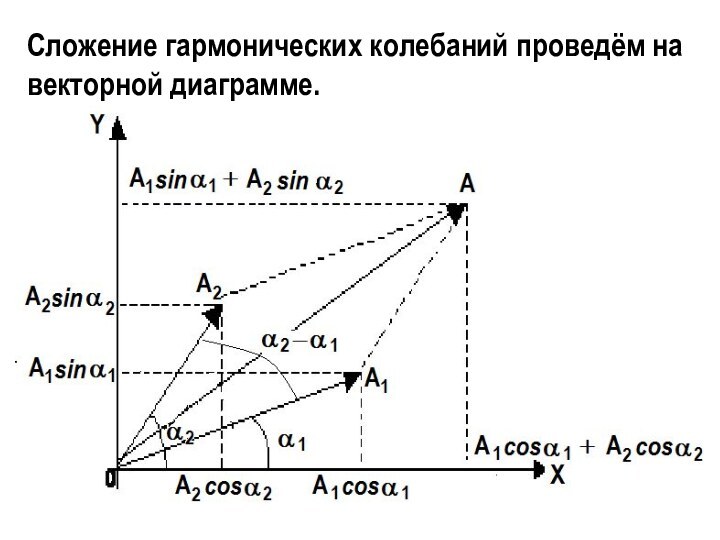
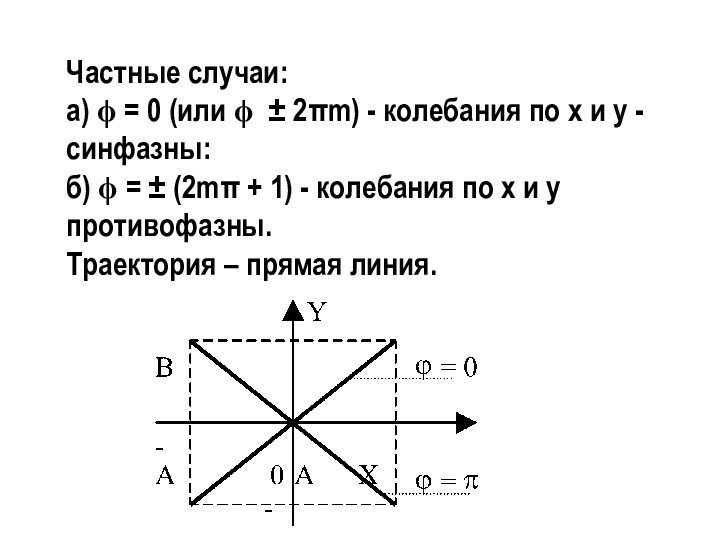
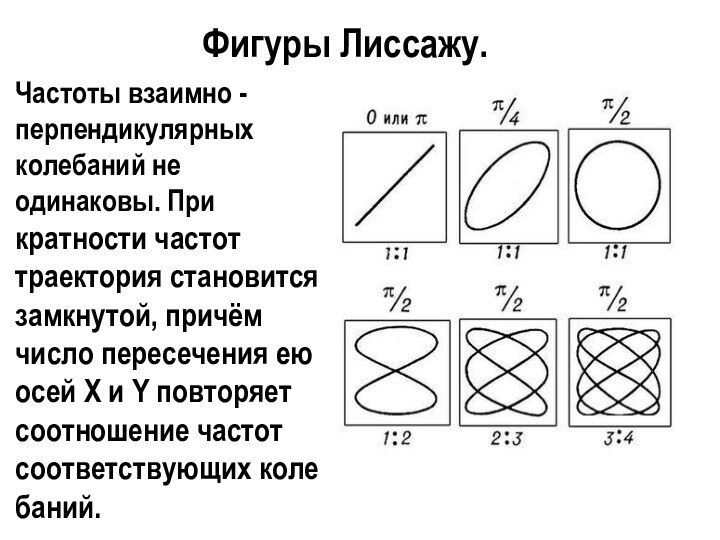
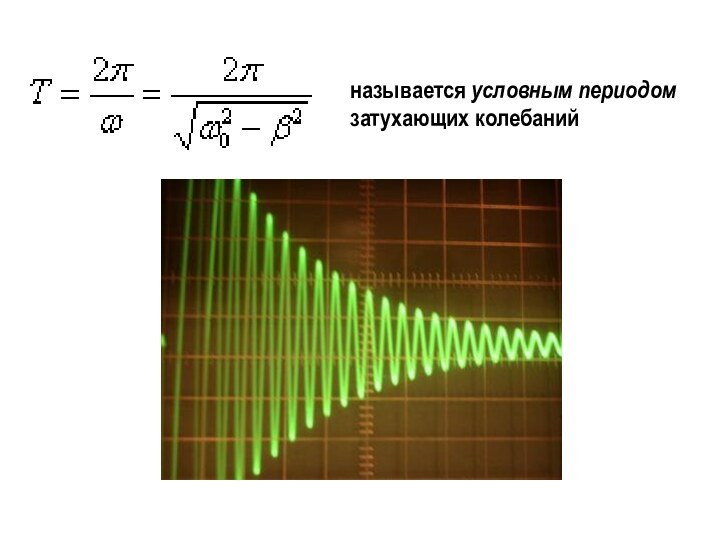
х1 = А1 cos (t + 1), х2

Результирующее колебание х = х1 + х2 должно быть гармони­ческим колебанием той же частоты , что и складываемые колебания, то есть х = А cos (t + ). Задача заключается в нахождении амплитуды А и начальной фазы  результи­рующего колебания.

результирующее колебание х = х1 + х2.
Амплитуду А резу­льтирующего

и начальную фазу  из

при их синфазности, т. е. при разности фаз кратной

 они оказываются в противофазе, и амплитуда результирующего колебания

Амин = А1 - А2 при 2 - 1 =  (2m + 1); m = 0, 1, 2, …

амплитуда резуль­тирующего колебания становится равной нулю.

Противофазные колебания с равными

А1cos ( + )t + 2)], где  

Результирующий вектор с амплитудой А = А1 + A2 будет при этом пульсировать по величине (по модулю) и вращаться с переменной скоростью.

= Аcos t + Аcos ( + )t =

сложения двух однонаправленных колебаний с близкими частотами:  -

заключается в исключении параметра t и связывании напрямую координат

найти чему равны sin t и cos t) получаем

2m) - колебания по х и у - синфазны:
б)

и у фазно-ортогональны.
Уравнение траектории: х2А2 + у2/В2 =

Случаи  = /2 и  = - /2 отличаются направлением движения точки по эллипсу или

окружности (по или
против часовой стрелки).

При кратности частот траектория становится замкнутой, причём число пересечения

– скорость движения.
Запишем второй закон Ньютона для затухающих

.

Получаем

):

где ω0

Для колебаний под действием упругой силы

; ;

времени t и t+T :





где β –

.

через период Т, называется логарифмическим декрементом затухания

Время релаксации – время, в течение которого амплитуда А уменьшается в e раз.
отсюда

в e раз. Тогда

Итак, логарифмический декремент затухания есть физическая величина, обратная числу колебаний, по истечении которых амплитуда А уменьшается в e раз.

уменьшение амплитуды, но и заметно увеличивается период колебаний. Когда

При колебаниях тело, возвращающееся в положение равновесия, имеет запас кинетической энергии. В случае апериодического движения энергия тела при возвращении в положение равновесия оказывается израсходованной на преодоление сил сопротивления, трения.

пропорциональна количеству колебаний, совершенных системой за время, за которое

колебательной системе изменяется по закону
где
- значение энергии в начальный

энергия мало изменяется, то при умножении этого выражения на

множителя 2 равна отношению энергии, запасенной в